Основное уравнение турбины

Поток жидкости, поступающий под некоторым углом на рабочее колесо турбины, меняет на рабочем колесе свое направление и уходит с него под другим углом, отличным от угла входа (рис. 6.1).

Рис. 6.1. Схема движения потока жидкости через рабочее колесо

Выделим в этом потоке элементарную струйку, скорость которой при входе на лопастную систему v₁, а при выходе - v₂. Разложим скорости v₁ и v₂ на три составляющие - по оси турбины v_z, по радиусу v_r и направлению вращения турбины v_u. Составляющая скорости v_u создает момент количества вращения жидкости относительно оси вращения рабочего колеса L = m^. v_u^.r, где m - масса жидкости в струйке с центром тяжести, имеющим радиус вращения r. За время dt в межлопастное пространство рабочего

колеса по струйке войдет жидкость массой dm = 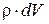, где dV - объем вошедшей жидкости. Поскольку жид-кость практически несжимаема, то за этот же промежуток времени в соответствии с уравнением неразрывности потока (2.3) из межлопастного пространства рабочего колеса по струйке выйдет такое же количество жидкости.

За счет взаимодействия струйки жидкости с лопастями рабочего колеса ее момент количества движения при входе на лопастную систему L₁ отличается от момента количества движения при выходе из лопастной системы L₂. Величина изменения момента количества движения dL за время dt определяется известным выражением

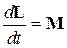, (6.1)

где М - вектор момента внешней силы относительно оси вращения. Для рассматриваемого случая выражение (6.1) можно записать в виде:

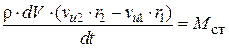, (6.2)

где M_ст - момент силы, действующий на струйку жидкости массой dm со стороны лопасти рабочего колеса. Индексы 1 и 2 указывают на соответствие входу и выходу из рабочего колеса. Помножим обе части равенства на угловую скорость рабочего колеса 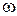. Учтем при этом, что расход струйки 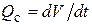, а действующий на лопасть рабочего колеса со стороны струйки момент силы M_тс = -M_ст. Тогда мощность N_тс, с которой струйка воздействует на турбину, равна

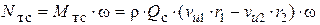. (6.3)

Мощность элементарной струйки N_с с учетом (2.10) и (2.13) определяется выражением

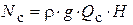, (6.4)

где H - действующий на рабочее колесо напор. Эффективность воздействия элементарной струйки на турбину характеризуется гидравлическим коэффициентом полезного действия :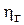

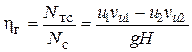, (6.5)

где u₁ 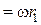и 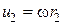- окружные скорости точек рабочего колеса. Выражение (6.5) можно еще представить в виде

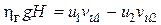. (6.6)

Поток в турбине состоит из множества элементарных струек. Если понимать под скоростями в уравнении (6.6) осредненные значения для всего потока, а под 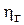- гидравлический КПД турбины, то данное уравнение справедливо для турбины в целом. Уравнение (6.6) носит название основного уравнения турбины. Впервые оно было выведено Леонардом Эйлером в 1751 г .