Формулы подобия для гидротурбин

Рассмотрим вывод формул подобия. Пусть через турбину (рис. 6.1), имеющую диаметр рабочего колеса D, проходит поток жидкости с осевой скоростью v_z. Поперечное сечение проточной части частично занято турбиной. Поэтому площадь сечения, через которое проходит жидкость, 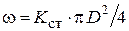, где К_ст - коэффициент стеснения сечения проточной части лопастями рабочего колеса, одинаковый для всей подобной серии турбин. Расход жидкости через турбину с учетом соотношения связи между скоростью потока и напором (5.10) можно представить в виде

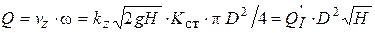, (6.9)

где 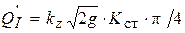- расход геометрически подобной турбины с диаметром рабочего колеса 1 м, работающей под напором 1 м, т.е. расход приведенной турбины в изогональном режиме. Параметр 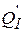называется приведенным расходом турбины. Следует отметить, что коэффициенты k_z и К_ст для приведенной и натурной турбин одинаковы только при выполнении требований полного гидродинамического подобия. Таким образом, формула (6.9) справедлива только для геометрически подобных натурной и приведенной турбин, работающих в гидродинамически подобных режимах.

С учетом (6.9) выражение для мощности турбины можно представить в виде

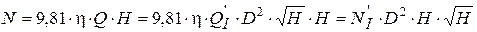, (6.10)

где параметр 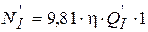называется приведенной мощностью турбины и соответствует мощности приведенной турбины в изогональном режиме. Здесь необходимо обратить внимание на то, что, как следует из (6.10), КПД натурной и приведенной турбин в изогональных режимах равны, т.е. .

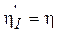Найдем теперь связь между частотами вращения натурной и приведенной турбин в изогональных режимах. Для этого воспользуемся основным уравнением турбины (6.6) и учтем, что 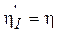. При преобразованиях используем выражения, связывающие угловую частоту вращения 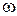с частотой вращения турбины в оборотах в минуту n, скорость потока 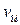, м/с, с напором H, м, (5.10), диаметры рабочего колеса D, м, с соответствующими радиусами турбины r, м:

; ; ; .

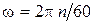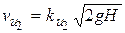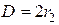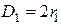Тогда выражение для гидравлического КПД турбины 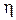можно представить в виде

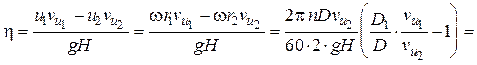
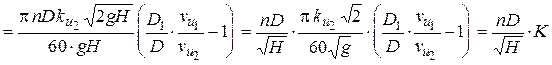, (6.11)

где 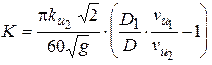и является величиной постоянной при выполнении требований гидродинамического подобия для всей серии геометрически подобных турбин.

Для приведенной турбины с учетом D = 1 м, H = 1 м выражение для КПД принимает вид

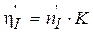. (6.12)

Уравняв выражения для КПД натурной и приведенной турбин, окончательно получаем

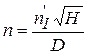. (6.13)

Параметр 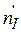обычно называют приведенной частотой вращения турбины.

На основании выведенных соотношений параметры любой натурной турбины можно пересчитать в параметры приведенной турбины (т.е. в приведенные параметры) и в параметры любой другой геометрически подобной турбины для изогонального режима работы. Приведенные параметры также можно пересчитать на параметры натурной турбины. Для нахождения приведенных параметров полученные соотношения удобно представить в виде

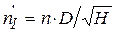, (6.14)

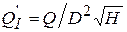, (6.15)

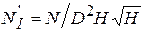, (6.16)

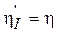. (6.17)

Выражения (6.9), (6.10), (6.13), (6.14) - (6.17), называются формулами подобия турбин в первом приближении, т.е. в предположении строгого выполнения требований полного гидродинамического подобия. На практике соблюсти полное гидродинамическое подобие между модельной и натурной турбинами не удается. Поэтому гидравлические КПД у турбины и ее модели не совпадают точно. С увеличением размера рабочего колеса КПД турбины обычно несколько возрастает.

При лабораторных испытаниях модельной турбины значения ее КПД 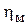для различных режимов достаточно точно измеряются экспериментально. Значения КПД натурной турбины 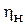уточняют по рекомендованным международной электротехнической комиссией полуэмпирическим формулам. Для поворотно-лопастных (ПЛ) турбин используется формула Хаттона:

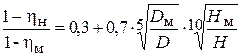. (6.18)

Для радиально-осевых (РО) турбин применяют формулу Муди:

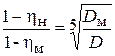. (6.19)

Для ковшовых турбин рекомендуется соотношение:

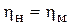. (6.20)

В (6.18) и (6.19) D_м, D и H_м , H - диаметры рабочего колеса и напоры для модельной и натурной турбин соответственно.