Механические и электромеханические характеристики электропривода с ДПТ НВ
Для получения основных соотношений для простейшей модели электропривода постоянного тока в статических (установившихся) режимах воспользуемся электрической схемой, приведённой на рис. 3.2.
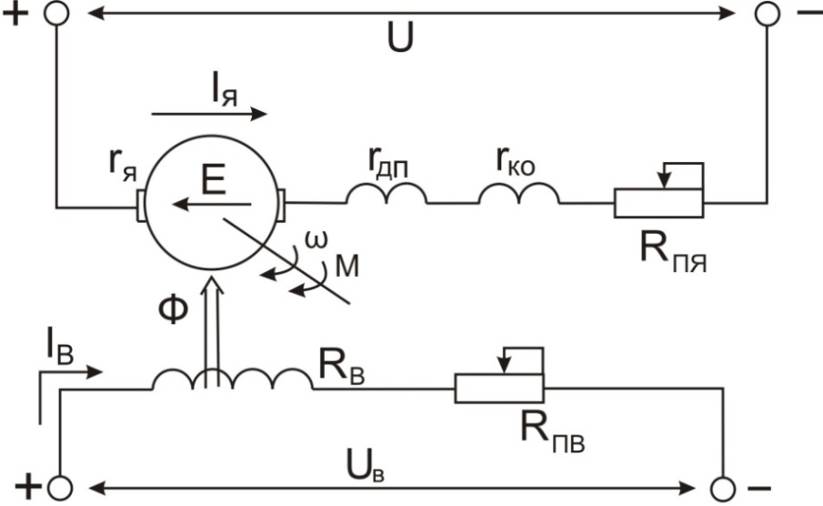
Рис. 3.2. Электрическая схема включения электропривода с двигателем постоянного тока независимого возбуждения (ДПТ НВ)
Будем считать, что якорь двигателя питается от источника напряжения бесконечно большой мощности. Взаимодействие тока в обмотке якоря с магнитным потоком 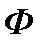 , создаваемым обмоткой возбуждения, расположенной на главных полюсах машины, приводит к возникновению электромагнитных сил, действующих на активные проводники обмотки и, следовательно, электромагнитному моменту
, создаваемым обмоткой возбуждения, расположенной на главных полюсах машины, приводит к возникновению электромагнитных сил, действующих на активные проводники обмотки и, следовательно, электромагнитному моменту
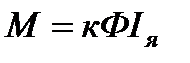 , (3.9)
, (3.9)
где 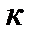 – конструктивный параметр машины.
– конструктивный параметр машины.
Под действием момента 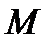 якорь двигателя вращается со скоростью
якорь двигателя вращается со скоростью 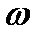 и в проводниках обмотки якоря наводится ЭДС в соответствии с законом Фарадея
и в проводниках обмотки якоря наводится ЭДС в соответствии с законом Фарадея
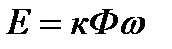 , (3.10)
, (3.10)
направленная встречно по отношению к току, а значит и напряжению.
Уравнение равновесия якорной цепи на основании закона Кирхгофа может быть записано в виде
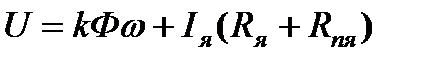 , (3.11)
, (3.11)
где 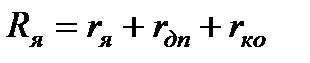 - полное сопротивление якоря двигателя, включая сопротивление обмотки добавочных полюсов
- полное сопротивление якоря двигателя, включая сопротивление обмотки добавочных полюсов 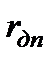 и компенсационной обмотки
и компенсационной обмотки 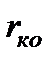 ;
;
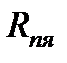 - добавочное сопротивление, введённое в общем случае в силовую цепь.
- добавочное сопротивление, введённое в общем случае в силовую цепь.
Тогда уравнение скоростной (электромеханической) характеристики 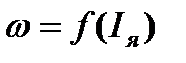 запишется так
запишется так
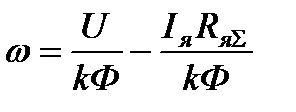 , (3.12)
, (3.12)
где 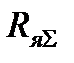 =
= 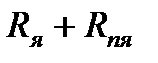 - полное сопротивление силовой цепи двигателя.
- полное сопротивление силовой цепи двигателя.
С учётом того, что
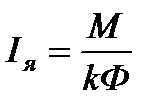 ,
,
уравнение механической характеристики двигателя может быть представлено в следующем виде
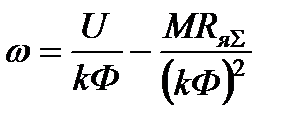 . (3.13)
. (3.13)
Конструктивный параметр машины постоянного тока определяется по формуле
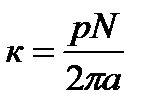 ,
,
где p – число пар главных полюсов;
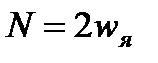 – число активных проводников обмотки якоря;
– число активных проводников обмотки якоря;
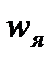 - число витков обмотки якоря;
- число витков обмотки якоря;
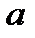 – число пар параллельных ветвей обмотки якоря.
– число пар параллельных ветвей обмотки якоря.
Эти параметры, а также сопротивления 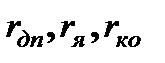 могут быть получены из каталожных данных или клиентского формуляра двигателя.
могут быть получены из каталожных данных или клиентского формуляра двигателя.
Величина 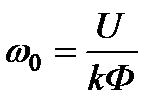 определяет скорость идеального холостого хода, которая зависит от
определяет скорость идеального холостого хода, которая зависит от 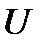 и
и 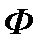 , а величина
, а величина
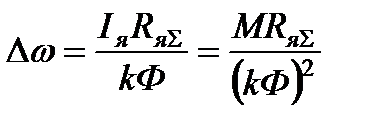
называется статическим падением скорости при действии момента статического сопротивления 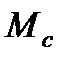 на валу двигателя. Тогда
на валу двигателя. Тогда
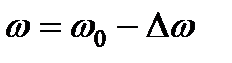
есть уравнение прямой, и может быть представлено графически на рис. 3.3.
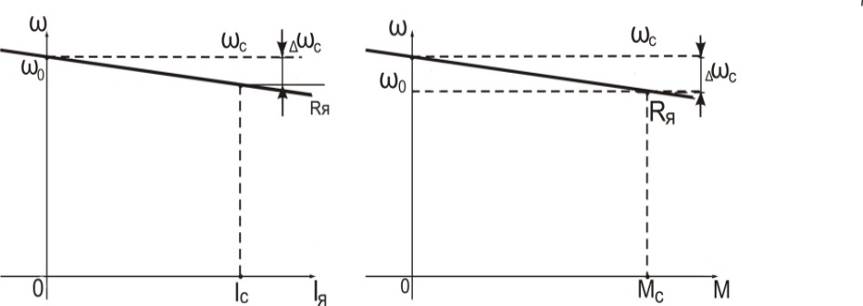
Рис. 3.3. Электромеханическая и механическая характеристики без дополнительного сопротивления в силовой цепи
Из уравнений (3.12), (3.13) могут быть получены уравнения характеристик в отрезках на осях (рис.3.4)
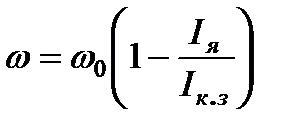 ; (3.14)
; (3.14)
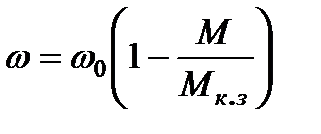 , (3.15)
, (3.15)
где 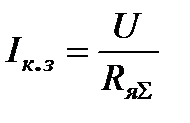 - ток короткого замыкания при
- ток короткого замыкания при  ;
;
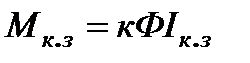 - момент короткого замыкания.
- момент короткого замыкания.
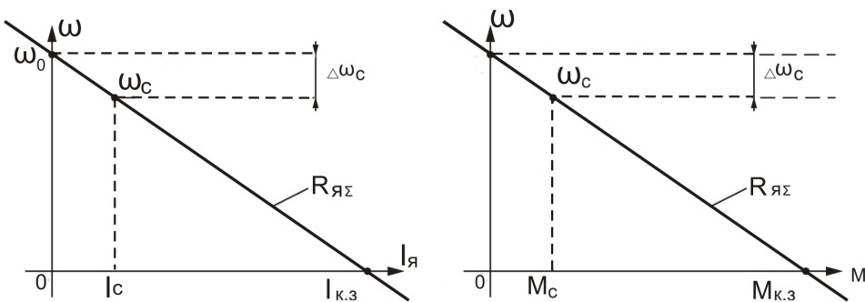
Рис. 3.4. Электромеханическая и механическая характеристики в отрезках на осях
Обратные зависимости 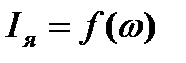 и
и 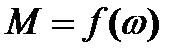 могут быть получены из (3.14) и (3.15)
могут быть получены из (3.14) и (3.15)
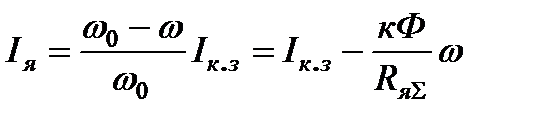 ; (3.16)
; (3.16)
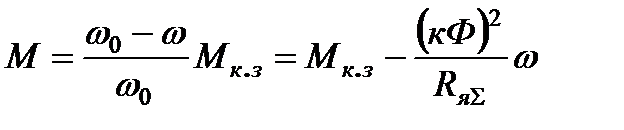 , (3.17)
, (3.17)
которые используются при аналитических расчётах.
Жёсткость механической характеристики
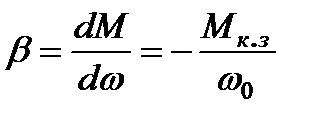 , Нм
, Нм  с (3.18)
с (3.18)
отрицательная величина, что говорит об уменьшении скорости с увеличением нагрузки, и определяется величиной момента короткого замыкания
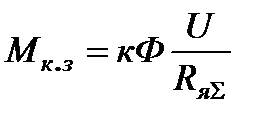
и скорости идеального холостого хода
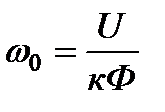 .
.
Тогда модуль статической жёсткости механической характеристики электропривода определяется в следующем виде
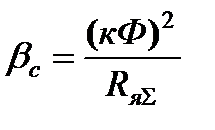 , (3.19)
, (3.19)
т.е. модуль статической жёсткости пропорционален квадрату магнитного потока Ф и обратно пропорционален полному сопротивлению якорной цепи привода 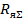 .
.
Дата добавления: 2019-02-08; просмотров: 1220;











