Вопрос 2. Статистические показатели динамики.

Понятие о рядах динамики.

Рядами динамики называются статистические данные, последовательно расположенные в хронологическом порядке, которые характеризуют развитие явления во времени.

Основные элементы ряда динамики:

1. Показатель времени – t. Это может быть определенная дата или временной интервал.

2. Уровень изучаемого явления – y.

Пример:

Существуют различные виды рядов динамики:

1. В зависимости от способа выражения уровней явления ряды динамики подразделяются на ряды абсолютных, относительных и средних величин.

Пример:

2. В зависимости от того, выражают ли уровни ряда динамики состояние явления на определенные моменты времени или на определенные интервалы времени, различают моментные и интервальные ряды динамики.

Пример:

3. В зависимости от расстояния между уровнями ряды динамики подразделяются на: ряды динамики с равноотстоящими уровнями и с не равноотстоящими уровнями.

Пример:

Требования к рядам динамики:.

1. Данные должны быть представлены за равновеликие периоды времени (относится к интервальным рядам динамики).

2. Изучаемые явления должны быть однородны в любом периоде.

3. Должны применяться одинаковые методики первичного учета и обобщения исходных данных.

4. Должны применяться одинаковые единицы измерения.

Вопрос 2. Статистические показатели динамики.

Для анализа рядов динамики применяются следующие показатели:

1. Абсолютный прирост;

2. Темп роста;

3. Темп прироста;

4. Абсолютное значение 1% прироста.

Показатели динамики могут вычисляться на постоянной или переменной базе сравнения.

При использовании постоянной базы все последующие уровни ряда сравниваются с базисным уровнем. Вычисляемые показатели в этом случае называются базисными.

При использовании переменной базы сравнения последующий уровень ряда сравнивается с предыдущим. Показатели динамики при этом называются цепными.

Пример:

1. Абсолютный прирост (сокращение).

Цепной 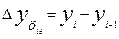(1)

Базисный 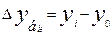(2), где:

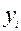- текущий уровень ряда динамики;

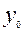- базисный уровень ряда динамики;

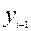- уровень ряда динамики, предшествовавший текущему;

2. Темп роста (сокращения).

Цепной 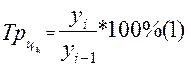(3)

Базисный 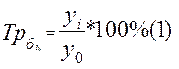(4)

3. Темп прироста (сокращения).

Цепной 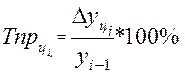(5)

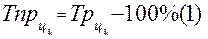(6)

Базисный 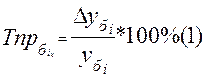(7)

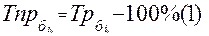(8)

4. Абсолютное значение 1 % прироста

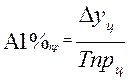(9)

Между цепными и базисными показателями динамики существует взаимосвязь:

1. Сумма цепных абсолютных приростов равна базисному абсолютному приросту последнего уровня ряда динамики.

2. Произведение цепных темпов роста равно последнему базисному темпу роста.