Характеристики основных типов линий передачи СВЧ

В СВЧ-диапазоне наибольшее распространение имеют следующие типы линий передачи:

1. Металлические волноводы.

2. Коаксиальные волноводы.

3. Полосковые линии.

Рассмотрим основные характеристики каждого из перечисленных типов линий передачи.

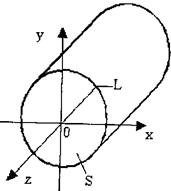Металлические волноводы.Поперечное сечение металлического волновода с произвольной формой поперечного сечения представлено на рис. 1.22,где L – контур, ограничивающий поперечное сечение волновода S. В таком волноводе могут существовать волны H – и Е –типов. Волны типа Н имеют продольную составляющую магнитного поля (H_z ¹ 0, E_z = 0).Волны типа Е имеют продольную составляющую электрического поля (H_z = 0, E_z ¹ 0).Каждая волна в волноводе характеризуется парой индексов m и n, физический смысл которых определяется формой поперечного сечения волновода.

Основной волной в волноводе является низшая H-волна, для которой критическая длина волны l_кр максимальная.

Аналитические выражения для составляющих полей в волноводе получаются в результате решения однородных волновых уравнений: для H-волн

D_^H_z + g²H_z = 0, dH_z / dn = 0на L;для Е-волн

D_^E_z + g²E_z = 0, dE_z = 0на L,

где D_^ =д² / дх² + д² / дy² – двумерный оператор Лапласа; g – поперечное волновое число; n – нормаль к контуру поперечного сечения волновода L.

По найденным H_z и E_z из уравнений Максвелла определяются остальные составляющие поля. При этом справедливы соотношения: длина волны в волноводе

;

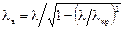продольная постоянная распространения

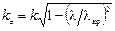(1.41)

фазовая скорость

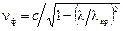; (1.42)

характеристическое сопротивление

для Н-волн ;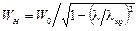

для Е-волн 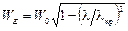, (1.43)

где W₀ = 120pОм – характеристическое сопротивление свободного пространства.

В этих выражениях k – волновое число, с – скорость света в вакууме.

Характеристическим сопротивлениемназывается отношение амплитуд поперечных составляющих электрического и магнитного полей бегущей волны. Следует отличать его от волнового сопротивления линии, которое определяется как отношение напряжения к току в линии с бегущей волной.

Рассматривают три режима работы волновода с данным типом волны:

1. Докритический режим (l < l_кр).

2. Критический режим (l = l_кр).

3. Закритический режим (l > l_кр).

В докритическом режимепроисходит распространение волны рассматриваемого типа. В этом режиме l_в, k_z и n_ф > с– действительные величины. В критическом режимераспространение прекращается, и l_в = ¥,k_z= 0 ,n_ф= ¥. В закритическом режиме,или в режиме отсечки,волновод эквивалентен для рассматриваемого типа волны чисто реактивной нагрузке. В данном режиме l_в, k_z и n_ф – чисто мнимые величины. При этом знак мнимой единицы при вычислении корня в выражениях (1.40) – (1.43) следует выбирать таким, чтобы при удалении от источника волны, находящейся в закритическом режиме, ее амплитуда экспоненциально убывала.

Прямоугольный волновод. Поперечное сечение такого волновода представлено на рис. 1.23. Для него критическая длина волны определяется соотношением

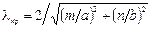. (1.44)

Решение однородных волновых уравнений может быть получено в виде:

для Н-волн

H_z = H₀cos(mpx / a) cos(npy / b) ,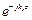

для E-волн

E_z = E₀cos(mpx / a) cos(npy / b) ,

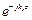где H₀, E₀ – амплитуда соответствующих продольных составляющих. Индексы ти n определяют количество вариаций поля на стенках а и bволновода соответственно. Основной волной в прямоугольном волноводе является волна Н₁₀. Для нее т = 1, n = 0, поэтому

l_кр = 2a, ;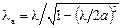

; ;

;

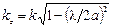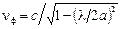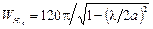H_z = H₀cos(px / a) 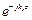, H_y = 0;

H_x = (jak_zH₀ / p)sin(px / a) 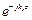, E_x = 0,

E_y = (-j2a 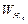H₀ / l)sin(px / a) .

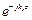Как известно, на внутренней поверхности стенок волновода протекают поверхностные токи 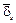, которые определяются соотношением:

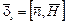. (1.46)

Отсюда следует, что поверхностный ток на стенках волновода перпендикулярен к касательным составляющим магнитного поля, а по величине плотность поверхностного тока равна касательной составляющей вектора магнитного поля.

При выборе размеров поперечного сечения волновода с основной волной исходят из условий, при которых волна Н₁₀находится в докритическом режиме, а высшие типы волн, в частности Н₂₀ и Н₀₁,находятся в закритическом режиме. Из этих условий следуют неравенства:

0,5l < a < l; b < 0,5l. (1.47)

Практические формулы для выбора размеров поперечного сечения волновода имеют вид

0,6l < a < 0,9l; b » 0,5а.(1.48)

Выбор размера b снизу ограничен величиной пробивного напряжения. При неограниченном уменьшении этого размера может наступить электрический пробой. Максимальная (предельная) мощность, пропускаемая волноводом с волной Н₁₀, определяется соотношением

P_max = 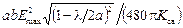[Вт],

где Е_mах = 30000 В/см – напряженность электрического поля, при кото­рой происходит пробой в воздухе. Допустимая передаваемая мощность Р_доп определяется как

Р_доп = (1/3...1/5)Р_mах (1.49)

Определив по приведенным формулам ориентировочные размеры а и b, далее по справочнику выбирают стандартный волновод, размеры которого наиболее близки к выбранным.

Для определения КПД волноводного тракта необходимо знать коэффициент затухания волны H_]0в волноводе. Этот коэффициент определяется формулой:

a = 8,686R_S 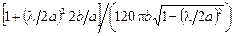[дБ/м],

где 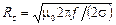– поверхностное сопротивление проводника; m₀= 4p 10^-7 Гн/м, s – удельная проводимость материала стенок волновода.

В табл. 1.4 приведены значения удельной проводимости s и активной составляющей поверхностного сопротивления R_Sдля металлов, наиболее часто используемых для изготовления волноводов.

Таблица 1.4

Металл	s, 1 / Ом×м	RS, Ом
Серебро Медь Алюминий Латунь	6,1×107 5,5×107 3,2×107 1,6×107	0,044 / 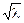0,047 / 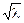0,061 / 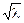0,086 /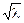

Примечание: значения длины волны l следует брать в сантиметрах.

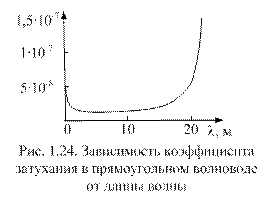На рис. 1.24 представлена зависимость коэффициента затухания aдля медного волновода (23x10 мм) от длины волны. Из графика следует, что a достигает минимума при некоторой оптимальной длине волны и резко возрастает с увеличением l по мере приближения ее к критическому значению l_кр При уменьшении l по сравнению с оптимальным значением потери увеличиваются. Это связано с увеличением значения поверхностного сопротивления R_S с ростом частоты.

Круглый волновод.Поперечное сечение круглого волновода характеризуется радиусом волновода а. Критическая длина волны для Н - и Е -волн определяется из соотношений

l_крH = 2pа / m_mn; l_крE = 2pа / b_mn,

где b_mn – n-й корень функции Бесселя т-го порядка; m_mn – n-й корень производной функции Бесселя m-го порядка. Применительно к круглому волноводу индексы т и n имеют следующий физический смысл: индекс т определяет количество вариаций поля по окружности волновода; индекс п определяет количество вариаций поля вдоль радиуса волновода.

Волн с индексом п = 0 не существует, так как они не удовлетворяют граничным условиям. Значения корня функции Бесселя или ее производной и l_кр некоторых типов волн приведены в табл. 1.5.

Таблица 1.5

Из таблицы, следует, что основной волной в круглом волноводе является волна H₁₁.Недостатком данного типа волны является неустойчивость ее поляризации, обусловленная наличием в реальном круглом волноводе различных неоднородностей (случайные неточности изготовления волновода).

В устройствах СВЧ на основе круглых волноводов находит применение волна E₀₁.

Коэффициент затухания для волн круглого волновода определяется соотношениями:

a = 8,686 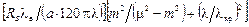[дБ/м],

– для H-волн;

a = 8,686 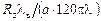[дБ/м]

– для Е -волн.

Характер зависимости а от длины волны такой же, как и для случая прямоугольного волновода (см.рис. 1.24).

Обобщение теории линий на волноводиые тракты. Волноводные тракты состоят обычно из отрезков регулярных волноводов, между ними расположены различные нерегулярности. Нерегулярность (или неоднородность) – это часть тракта, в которой имеется скачкообразное или плавное изменение формы или размеров поперечного сечения волновода. Определение полей и характеристик нерегулярностей требует решения уравнений Максвелла для заданных граничных условий. При этом используются методы прикладной электродинамики в сочетании с различными численными методами, ориентированными на ЭВМ различного класса. Сложность решения задачи состоит в том, что вблизи неоднородности поле представляет собой су­перпозицию полей всех типов волн в волноводе. При удалении от неоднородности волны высших типов, находящиеся в закритическом режиме, быстро затухают, и на расстоянии порядка длины волны поле определяется только падающей и отраженной волнами основного типа. Следовательно, волны высших типов локализованы вблизи неоднородности и образуют так называемое реактивное поле, накапливающее в себе определенное количество электромагнитной энергии. Если на данной частоте энергия закритических волн, накопленная электрическим полем, превышает энергию закритических волн, накопленную магнитным полем, то такая неоднородность имеет емкостной характер сопротивления, в противном случае – индуктивный. В случае равенства энергий, накопленных электрическим и магнитным полями, неоднородность является резонансной. Эти сопротивления и проводимости включаются в линию, эквивалентную волноводу, параллельно, последовательно или в какой-либо комбинации в зависимости от характера неоднородности. Если неоднородность невызывает скачка напряжения до и после нее, то эквивалентная реактивность включается в линию параллельно, если нет скачка тока, то последовательно. Сопротивления и проводимости, характеризующие неоднородность, обычно нормируют, т.е. относят к волновому сопротивлению эквивалентной линии:

Z_норм = Z_{не норм} / W; Y_норм = Y_{не норм} / W.

Строгие методы расчета, применяемые для анализа волноводных неоднородностей, позволяют определить все их эквивалентные параметры и характеристики. Эквивалентные схемы многих волноводных нерегулярностей приведены в различных справочниках, например, в монографии Гупта К., Гардша Р., Чадка Р. "Машинное проектирование СВЧ-устройств" / Пер. с англ. – М.: Радио и связь, 1987. – 432 с.

Для инженерного расчета волноводных трактов с регулярными и нерегулярными участками используют эквивалентные схемы, значительно упрощающие расчеты. При этом регулярный волновод заменяют эквивалентной двухпроводной линией. Неоднородности представляют в виде сосредоточенных элементов, включенных в эту линию, а для расчета всей цепи используют теорию длинных линий.

С целью определения параметров длинной линии, эквивалентной волноводу, проведем математическую аналогию между ними.

Полный продольный ток, протекающий по проводам линии и по стенкам волновода, в любом сечении равен нулю, т.е. для линии I_1э + I_2э = 0; для волновода 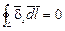, , 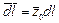где 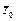– единичный вектор, параллельный оси z. Определим токи I_1э и I_2э в линии, эквивалентной волноводу:

;

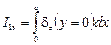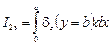
где d_z – продольная составляющая поверхностного тока на стенках волновода. Эти токи равны по величине и противоположны по знаку из-за различной ориентации поверхностного тока на верхней и нижней станках волновода. Определим напряжение в линии, эквивалентной волноводу, как интеграл вдоль силовой линии поперечной составляющей электрического поля бегущей волны с максимальной напряженностью. В случае прямоугольного волновода с волной Н₁₀:

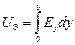при x = a / 2.

Так как в рассматриваемом случае d_z(y = 0) = -d_z(y = b) = = H_xmsin(px / a), E_y = E_ymsin(px / a), то для токов I₁, I₂ и напряжения U, получим:

I_1э = -I_2э = 2aH_xm / p; U_э = E_ymb.

Найдем волновое сопротивление эквивалентной линии, учитывая связь между амплитудами поперечных составляющих полей E_ym = W_H10H_xm, где W_H10 – характеристическое сопротивление волн Н₁₀ (1.45):

W_э = U_э / I_э = W_H10pb / (2a).

Итак, регулярный волновод, в котором распространяется одна волна, эквивалентен дисперсионной линии с током I_1э, напряжением U_э, волновым сопротивлением W_э, постоянной распространения b_э = 2p / l_ви фазовой скоростью 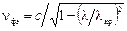. Замена волновода эквивалентной линией справедлива в докритическом режиме, l < l_кр. Если в волноводе одновременно распространяются несколько типов волн, то он эквивалентен соответствующему числу не связанных одна с другой двухпроводным линиям, так как волны в волноводах без потерь ортогональны (взаимно не связаны), т.е. энергия, переносимая какой-либо волной по регулярному волноводу, не передается в другие типы волн.

Коаксиальные волноводы. На практике наибольшее распространение имеет круглый коаксиальный волновод, или просто коаксиал, поперечное сечение которого показано на рис. 1.29. Пространство между внешним и внутренним проводниками может быть заполнено воздухом или другим диэлектриком с относительной диэлектрической проницаемостью e_r. Основной волной является волна типа Т (поперечная электромагнитная волна), структура силовых линий которой показана на рис. 1.25. Волновое сопротивление для T-волны определяется формулой 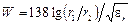. Для того чтобы все высшие типы волн находились в закритическом режиме, необходимо выполнение условия:

p(r₁ + r₂) < l (1.50)

Потери aв коаксиальном волноводе складываются из потерь в диэлектрике a_д ипотерь в проводниках a_п: a = a_д + a_п. Значения a_д иa_п могут быть найдены из соотношений:

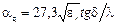[дБ/м];

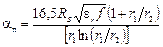[дБ/м], (1.51)

где tgd – тангенс угла диэлектрических потерь; f – частота колебаний в гигагерцах (1ГГц = 10⁹Гц).

Максимальная мощность, передаваемая по коаксиалу в режиме бегущей волны, определяется соотношением:

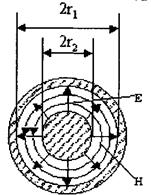
P_max =E²_maxr²₂ln(r₁ / r₂) / 120[кВт]. (1.52)

Допустимая мощность определяется из (2.10). На рис. 1.26 представлены зависимости затухания, допустимой передаваемой мощности и волнового сопротивления коаксиала от отношения r₁ / r₂.Из графиков следует, что для уменьшения потерь и увеличения пропускаемой мощности желательно пропорционально увеличивать размеры r₁и r₂. Это увеличение ограничивается условием одноволновости коаксиала (1.50). Оптимальное соотношение радиусов проводников коаксиала (r₁ / r₂ = 3,6), обеспечивает минимальные потери при минимальном волновом сопротивлении W_орt = 100 Ом. При r₁ / r₂ = 1,65 обеспечивается максимальная электрическая прочность при W_орt = 30 Ом. В качестве стандартных выбраны следующие значения волновых сопротивлений коаксиалов: 50, 75, 100 и 150 Ом.

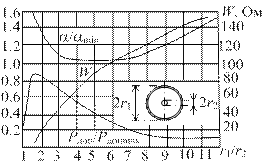
Рис 1.26. Зависимость затухания, допустимой передаваемой мощности и волнового сопротивления коаксиала от отношения r₁ / r₂

Полосковые линии.На практике наибольшее распространение имеют симметричная и несимметричная полосковые линии, геометрия поперечных сечений которых представлена на рис. 1.27.Пространство

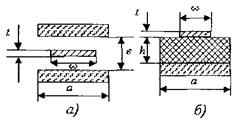
Рис. 1.27.Поперечные сечения полосковых линий: а – симметричной; б– несимметричной

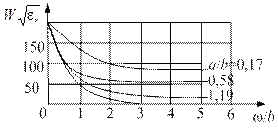
Рис. 1.28. Зависимость волнового сопротивления симметричной полосковой линии от ширины полоски при различных размерах экрана

между пластинами полосковой линии может быть заполнено воздухом или другим диэлектриком. Основной волной является волна типа Т, структура силовых линий которой показана на рис. 1.3.Для существования только волны типа Т в симметричной полосковой линии должны быть выполнены условия: 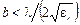, 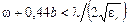.Для несимметричной полосковой линии условия имеют следующий вид: 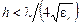, 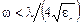. Волновое сопротивление полосковой ли­нии сложным образом зависит от ее геометрических размеров, и эта зависимость в элементарных функциях не выражается. На рис. 1.28представлена зависимость волнового сопротивления симметричной идеально проводящей полосковой линии от отношения w / b при t = 0. Параметром графиков является нормированная ширина пластины а / b.

Потери aполосковых линий складываются, как и в коаксиальном волноводе, из потерь в диэлектрике a_д и потерь в проводниках a_п:

a = a_л + a_п.

Значения a_д и a_п могут быть найдены из соотношений, приведенных, например, в книге "Справочник по расчету и конструированию СВЧ полосковых устройств"/ С.И. Бахарев и др. / Под ред. В.И. Вольмана. – М.: Радио и связь, 1982. – 328 с. Графики, представленные на рис. 1.32 – 1.36, взяты из этой книги.

Следует отметить, что предельная мощность, передаваемая по полосковым линиям, существенно меньше мощности, передаваемой по полым и коаксиальным волноводам. Это объясняется значительной концентрацией энергии поля вблизи края полоски, малым зазором между полоской и экраном, рассеянием мощности в диэлектрике линии, а также малой шириной полоски.