Теория регулярных линий передачи
На практике наибольшее распространение получили отрезки регулярных линий передачи той или иной длины. Если длина регулярной линии передачи существенно превышает длину волны в линии lл, то такая линия называется длинной. Характерной особенностью длинных линий является возможность существования в них двух волн, распространяющихся навстречу друг другу. Одна из этих волн образуется подключенным к линии генератором электромагнитных колебаний и называется падающей. Другая волна образуется из-за отражения падающей волны от нагрузки, подключенной к противоположному концу линии, и называется отраженной. Отраженная волна распространяется в направлении, обратном падающей волне. Все разнообразие процессов, происходящих в длинной линии, определяется амплитудно-фазовыми соотношениями между падающей и отраженной волнами.
Составление и решение дифференциальных уравнений длинной линии.Рассмотрим двухпроводную длинную линию, представленную на рис. 1.9, где Zн = Rн + jХн– комплексное сопротивление нагрузки; z – продольная координата линии, отсчитываемая от места подключения нагрузки.

Рис. 1.9. Схема вывода дифференциальных уравнений длинной линии
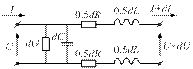
Рис. 1.10. Эквивалентная схема участка длиной dz
Из электродинамики известно, что линия передачи может быть охарактеризована ее погонными параметрами: R1 – погонное сопротивление, Ом/м; G1, – погонная проводимость, 1/Ом×м; L1, – погонная индуктивность, Гн/м; С1, – погонная емкость, Ф/м. Погонные сопротивление R1 и проводимость G1, зависят от проводимости материала проводов и качества диэлектрика, окружающего эти провода, соответственно. Чем меньше тепловые потери в металле проводов и в диэлектрике, тем меньше, соответственно, R1и G1. Погонные индуктивность L1 и емкость С1, определяются формой и размерами поперечного сечения проводов, а также расстоянием между ними. Выделим из линии элементарный участок бесконечно малой длины dz и рассмотрим его эквивалентную схему (рис. 1.10).
На этой схеме стрелками обозначены направления отсчета напряжения U и тока I в линии; dU и dI – приращения напряжения и тока в линии на элементе длины dz . Значения параметров схемы определяются соотношениями:
dR = R1dz; dG = G1dz; (1.1)
dC = C1dz; dL = L1dz.
Используя эквивалентную схему, запишем выражения для приращений напряжения и тока:
dU = I (dR + jwdL),
dI = U (dG + jwdC).
Подставляя сюда значения параметров схемы из (1.1), получаем:
dU = IZ1dz, dI = UY1dz,
где Z1 = R1 + jwL1, Y1 = G1+ jw C1 – погонные комплексные сопротивление и проводимость линии.
Из последних соотношений находим:
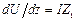 ;
; 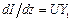 (1.2)
(1.2)
Эти соотношения называются телеграфными уравнениями длинной линии, они определяют связь между током и напряжением в любом сечении линии.
Решим телеграфные уравнения относительно напряжения и тока. Для этого продифференцируем их по z:
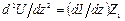 ;
; 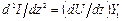
Данные соотношения являются математическим определением регулярности длинной линии. Смысл соотношения (1.4) состоит в неизменности вдоль линии ее погонных параметров.
Подставляя в (1.3) значения производных напряжения и тока из (1.2), после преобразований получаем:
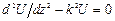 ,
, 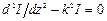 (1.5)
(1.5)
где k – коэффициент распространения волны в линии, 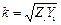 .
.
Соотношения (1.5) называются однородными волновыми уравнениями длинной линии. Их решения известны и могут быть записаны в виде
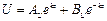 ,
, 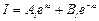 (1.6)
(1.6)
где АU , BU и АI , BI – коэффициенты, имеющие единицы измерения напряжения и тока соответственно, смысл которых будет ясен ниже.
Решения волновых уравнений в виде (1.6) имеют весьма характерный вид: первое слагаемое в этих решениях представляет собой падающую волну напряжения или тока, распространяющуюся от генератора к нагрузке, второе слагаемое – отраженную волну, распространяющуюся от нагрузки к генератору. Таким образом, коэффициенты АU, АI представляют собой комплексные амплитуды падающих волн напряжения и тока соответственно, а коэффициенты BU, BI – комплексные амплитуды отраженных волн напряжения и тока соответственно. Поскольку часть мощности, передаваемой по линии, может поглощаться в нагрузке, амплитуды отраженных волн не должны превышать амплитуды падающих:
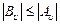 ;
; 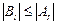 .
.
Направление распространения волн в (1.6) определяется знаком в показателях степени экспонент: "плюс" – волна распространяется в отрицательном направлении оси z; "минус" – в положительном направлении оси z (см. рис. 1.9).Так, например, для падающей волны можно записать:
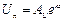 ;
; 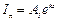 . (1.7)
. (1.7)
Коэффициент распространения волны в линии k в общем случае является комплексной величиной и может быть представлен следующим образом:
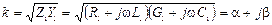 , (1.8)
, (1.8)
где a – коэффициент затухания волны в линии; b – коэффициент фазы.
Тогда соотношение (1.7) можно переписать в виде:
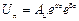 ;
; 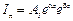 . (1.9)
. (1.9)
Коэффициент затухания a определяет скорость уменьшения амплитуды волны при распространении вдоль линии. Коэффициент фазы b определяет скорость изменения фазы волны вдоль линии.
Так как при распространении падающей волны на длину волны в линии lл фаза волны изменяется на 2p, то коэффициент фазы можно связать с длиной волны lл соотношением
b = 2p / lл. (1.10)
При этом фазовая скорость волны в линии uф определяется через коэффициент фазы:
uф = w / b. (1.11)
Определим коэффициенты А и В, входящие в решения (1.6) волновых уравнений, через значения напряжения Uни тока Iн на нагрузке. Это является оправданным, поскольку напряжение и ток на нагрузке практически всегда можно измерить с помощью измерительных приборов. Воспользуемся первым из телеграфных уравнений (1.2) и подставим в него напряжение и ток из (1.6). Тогда
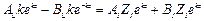 .
.
Сравнив коэффициенты при экспонентах с одинаковыми показателями степеней, получим:
AI = AU / W, BI = -BU / W, (1.12)
где , 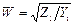 – волновое сопротивление линии. Волновым сопротивлением линии передачи называется отношение напряжения к току в бегущей волне.
– волновое сопротивление линии. Волновым сопротивлением линии передачи называется отношение напряжения к току в бегущей волне.
Перепишем (1.6) с учетом (1.12):
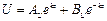 ;
; 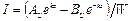 (1.13)
(1.13)
Для определения коэффициентов А и В в этих уравнениях воспользуемся условиями в конце линии z = 0, U(z = 0) = Uн. Тогда из (1.13) при z = 0 найдем
АU = 0,5(Uн + IнW); BU = 0,5(Uн - IнW). (1.14)
Подставив полученные значения коэффициентов из (1.14) в (1.13), после преобразовании получим:
U = Uн ch(kz) + IнWsh(kz); I = Iн ch(kz) + (Uн / W)sh(kz).
При выводе (1.15) учтены определения гиперболических синуса и косинуса:
sh(kz) = (ekz – e-kz)/2;
ch(kz) = (ekz + e-kz)/2.
Соотношения для напряжения и тока (1.15), так же как и (1.6), являются решениями однородных волновых уравнений. Их отличие состоит в том, что напряжение и ток в линии в соотношении (1.6) определены через амплитуды падающей и отраженной волн, а в (1.15) – через напряжение и ток на нагрузке.
Закономерности изменения напряжения и тока вдоль линии.Рассмотрим простейший случай, когда напряжение и ток в линии определяются только падающей волной, а отраженная волна отсутствует. Тогда в (1.6) следует положить ВU = 0, ВI = 0:
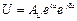 ;
; 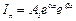 .
.
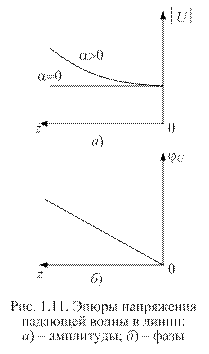 На рис. 1.11 представлены эпюры изменения амплитуды |U|и фазы jU напряжения вдоль линии. Эпюры изменения амплитуды и фазы тока имеют такой же вид. Из рассмотрения эпюр следует, что при отсутствии в линии потерь (a= 0) амплитуда напряжения в любом сечении линии остается одной и той же. При наличии потерь в линии (a > 0)часть переносимой мощности преобразуется в тепло (нагревание проводов линии и окружающего их диэлектрика). По этой причине амплитуда напряжения падающей волны экспоненциально убывает в направлении
На рис. 1.11 представлены эпюры изменения амплитуды |U|и фазы jU напряжения вдоль линии. Эпюры изменения амплитуды и фазы тока имеют такой же вид. Из рассмотрения эпюр следует, что при отсутствии в линии потерь (a= 0) амплитуда напряжения в любом сечении линии остается одной и той же. При наличии потерь в линии (a > 0)часть переносимой мощности преобразуется в тепло (нагревание проводов линии и окружающего их диэлектрика). По этой причине амплитуда напряжения падающей волны экспоненциально убывает в направлении
распространения.
Фаза напряжения падающей волны jU = bz изменяется по линейному закону и уменьшается по мере удаления от генератора.
Рассмотрим изменение амплитуды и фазы, например, напряжения при наличии падающей и отраженной волн. Для упрощения положим, что потери в линии отсутствуют, т.е. a = 0. Тогда напряжение в линии можно представить в виде
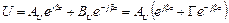
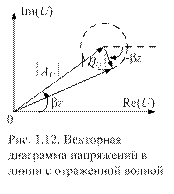 где G = ВU / АU – комплексный коэффициент отражения по напряжению. Он характеризует степень согласования линии передачи с нагрузкой. Модуль коэффициента отражения изменяется в пределах: 0 £ |Г| £ 1. При этом |Г| = 0, если отражения от нагрузки отсутствуют и ВU = 0; |Г| = 1, если волна полностью отражается от нагрузки, т.е. |ВU| = |АU|.
где G = ВU / АU – комплексный коэффициент отражения по напряжению. Он характеризует степень согласования линии передачи с нагрузкой. Модуль коэффициента отражения изменяется в пределах: 0 £ |Г| £ 1. При этом |Г| = 0, если отражения от нагрузки отсутствуют и ВU = 0; |Г| = 1, если волна полностью отражается от нагрузки, т.е. |ВU| = |АU|.
Соотношение (1.16) представляет собой сумму падающей и отраженной волн. Отобразим напряжение на комплексной плоскости в виде векторной диаграммы, каждый из векторов которой определяет падающую, отраженную волны и результирующее напряжение (рис. 1.12). Из диаграммы видно, что существуют такие поперечные сечения линии, где падающая и отраженная волны складываются в фазе. Напряжение в этих сечениях достигает максимума, величина которого равна сумме амплитуд падающей и отраженной волн: Umax = |АU| + |ВU|. Кроме того, существуют такие поперечные сечения линии, где падающая и отраженная волны складываются в противофазе. При этом напряжение достигает минимума: Umin = |АU| - |ВU|.
Если линия нагружена на сопротивление, для которого |Г| = 1, т.е. амплитуда падающей и отраженной волн равны |ВU| = |АU|, то в этом случае Umax = 2|АU|, а Umin = 0. Напряжение в такой линии изменяется от нуля до удвоенной амплитуды падающей волны. На рис. 1.13 представлены эпюры изменения амплитуды и фазы напряжения вдоль линии при наличии отраженной волны.
По эпюре напряжения судят о степени согласования линии с нагрузкой. Для этого вводятся понятия коэффициента бегущей волны Kбв и коэффициента стоячей волны Kсв:
Kбв = Umin / Umax = (|АU| - |ВU|) / (|АU| + |ВU|) =
= (1 - |Г|) / (1 + |Г|) (1.17)
Kсв = 1 / Kбв (1/18)
Эти коэффициенты, судя по определению, изменяются в пределах: 0 £ Kбв £ 1, 1 £ Kсв < ¥.
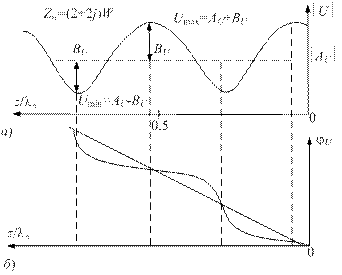
Рис. 1.13. Эпюры напряжения в линии с отраженной волной:
а) – амплитуды; б) – фазы
На практике наиболее часто используется понятие коэффициента стоячей волны, так как современные измерительные приборы (панорамные измерители Kсв)на индикаторных устройствах отображают изменение именно этой величины в определенной полосе частот.
Важной характеристикой длинной линии является входное сопротивление линии Zвх=Rвх + jXвх, которое определяется в каждом сечении линии как отношение напряжения к току в этом сечении:
Zвх(z) = U(z) / I(z). (1.19)
Так как напряжение и ток в линии изменяются от сечения к сечению, то и входное сопротивление линии изменяется относительно ее продольной координаты z. При этом говорят о трансформирующих свойствах линии, а саму линию рассматривают как трансформатор сопротивлений. Подробнее свойство линии трансформировать сопротивления будет рассмотрено ниже.
Режимы работы длинной линии без потерь.Различают три режима работы линии: режим бегущей волны, режим стоячей волны, режим смешанных волн.
Режим бегущей волны характеризуется наличием только падающей волны, распространяющейся от генератора к нагрузке. Отраженная волна отсутствует. Мощность, переносимая падающей волной, полностью выделяется в нагрузке. В этом режиме ВU = 0, |Г| = 0, Kбв = Kсв= 1.
Режим стоячей волны характеризуется тем, что амплитуда отраженной волны равна амплитуде падающей |ВU| = |АU|, т.е. энергия падающей волны полностью отражается от нагрузки и возврашается обратно в генератор. В этом режиме |Г| = 1, Kсв= ¥, Kбв = 0.
В режиме смешанных волн амплитуда отраженной волны удовлетворяет условию 0 < |ВU| < |АU|, т.е. часть мощности падающей волны теряется в нагрузке, а остальная часть в виде отраженной волны возвращается обратно в генератор. При этом 0 < |Г| < 1, 1 < Kсв < ¥, 0 < Kбв < 1. Следует отметить, что режимы бегущей и стоячей волн не реализуемы на практике и являются математической абстракцией. Возможно приближение к указанным режимам в той или иной степени. Это объясняется наличием в реальных линиях передачи тепловых потерь, различных нерегулярностей и неоднородностей, обусловленных конечной точностью изготовления линии, наличием элементов крепления и т.п., вызывающих появление отраженной волны.
Свойства линии без потерь.В линии без потерь погонные параметры R1 = 0 и G1 = 0. Поэтому для коэффициента распространения k и волнового сопротивления W получим
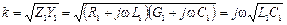 ;
;
a = 0; b = 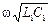 ;
; 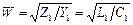 . (1/20)
. (1/20)
С учетом этого выражения для напряжения и тока (1.15) примут вид:
U = Uн cos(bz) + IнWsin(bz);
I = Iн cos(bz) + (Uн / W) sin (bz). (1.21)
При выводе этих соотношений учтено, что ch(jbz) = cos(bz); sh(jbz) = jsin(bz). Рассмотрим конкретные примеры работы линии без потерь на простейшие нагрузки.
Разомкнутая линия. В этом случае ток, протекающий через нагрузку равен нулю (Iн = 0), поэтому выражения для напряжения, тока и входного сопротивления в линии принимают вид:
U = Uн cos(bz); I = j(Uн / W) sin (bz);
Zвх = U / I = -jWctg(bz) = jXвх; b = 2p / lл. (1.22)
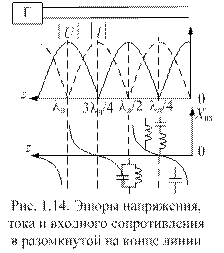 На рис. 1.14 эти зависимости проиллюстрированы графически. Из соотношений (1.22) и графиков следует:
На рис. 1.14 эти зависимости проиллюстрированы графически. Из соотношений (1.22) и графиков следует:
- в линии, разомкнутой на конце, устанавливается режим стоячей волны, напряжение, ток и входное сопротивление вдоль линии изменяются по периодическому закону с периодом lл / 2;
- входное сопротивление разомкнутой линии является чисто мнимым, за исключением точек с координатами z = nlл / 4, n = 0, 1, 2,...;
- если длина разомкнутой линии меньше lл /4, то такая линия эквивалентна емкости;
- разомкнутая на конце линия длиной lл эквивалентна последовательному резонансному на рассматриваемой частоте контуру и имеет нулевое входное сопротивление.
Замкнутая линия.В этом случае напряжение на нагрузке равно нулю (Uн = 0), поэтому напряжение, ток и входное сопротивление в линии принимают вид:
U = jIнWsin(bz), I = Iнcos(bz);
Zвх=U / I = jWtg(bz) = -jXвх. (1.23)
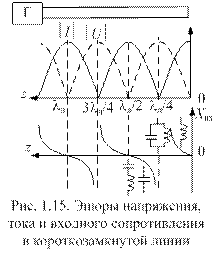 На рис. 1.15 эти зависимости проиллюстрированы графически.
На рис. 1.15 эти зависимости проиллюстрированы графически.
Используя результаты предыдущего раздела, нетрудно самостоятельно сделать выводы о трансформирующих свойствах коротко-замкнутой линии. Отметим лишь, что в замкнутой линии также устанавливается режим стоячей волны. Отрезок короткозамкнутой линии, длиной меньше lл / 4, имеет индуктивный характер входного сопротивления, а при длине lл / 4
такая линия имеет бесконечно большое входное сопротивление на рабочей частоте. Это свойство короткозамкнутого четвертьволнового отрезка линии позволяет использовать его в практических устройствах как «металлический изолятор».
Линия, нагруженная на емкость.Как следует из анализа работы разомкнутой линии, каждой емкости С на данной частоте «можно поставить в соответствие отрезок разомкнутой линии длиной меньше lл / 4. Емкость С имеет емкостное сопротивление jXC = j / wС. Приравняем величину этого сопротивления к входному сопротивлению разомкнутой линии длиной l < lл / 4:
-j / wС = -jWctg(bl).
Отсюда находим длину линии l, эквивалентную по входному сопротивлению емкости С:
l = (l / b)arctg[wCW].
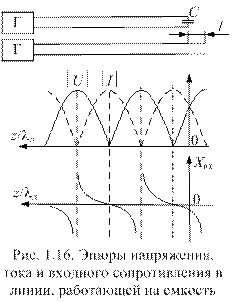
Зная эпюры напряжения, тока и входного сопротивления разомкнутой линии, восстанавливаем их для линии, работающей на емкость (рис. 1.16). Из эпюр следует, что в линии, в этом случае, устанавливается режим стоячей волны.
При изменении емкости эпюры сдвигаются вдоль оси z. В частности, при увеличении емкости емкостное сопротивление уменьшается, напряжение на емкости падает, и все эпюры сдвигаются вправо, приближаясь к эпюрам, соответствующим короткозамкнутой линии. При уменьшении емкости эпюры сдвигаются влево, приближаясь к эпюрам, соответствующим разомкнутой линии.
Линия, нагруженная на индуктивность.Как следует из анализа работы замкнутой линии, каждой индуктивности L на данной частоте wможно поставить в соответствие отрезок замкнутой линии длиной меньше lл / 4. Индуктивность L имеет индуктивное сопротивление jXL = jwL.Приравняем это сопротивление к входному сопротивлению замкнутой линии длиной l < lл / 4: jwL = jWtg(bl). Отсюда находим длину линии l, эквивалентную по входному сопротивлению индуктивности L:
l = (l /b)arctg(wL / W).
Зная эпюры напряжения, тока и входного сопротивления замкнутой на конце линии, восстанавливаем их для линии, работающей на индуктивность (рис. 1.17). Из эпюр следует, что в линии, работающей на индуктивность, также устанавливается режим стоячей волны. Изменение индуктивности приводит к сдвигу эпюр вдоль оси z . Причем с увеличением L эпюры сдвигаются вправо, приближаясь к эпюрам холостого хода, а с уменьшением L – влево по оси z, стремясь к эпюрам короткого замыкания.

Линия, нагруженная на активное сопротивление.В этом случае ток и напряжение на нагрузке Rнсвязаны соотношением Uн = IнRн. Выражения для напряжения и тока в линии (1.21) принимают вид:
U = Uн cos(bz) + jIн(W / Rн)sin(bz);
I = Iн cos(bz) + j(Rн / W) sin (bz).
Рассмотрим работу такой линии на примере анализа напряжения. Найдем из (1.24) амплитуду напряжения в линии:
|U| = Uн 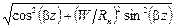 . (1.25)
. (1.25)
Отсюда следует, что можно выделить три случая: 1) Rн = W;2) Rн > W; 3) Rн < W.
Впервом случае из (1.25) следует |U| = Uн,т.е. напряжение вдоль линии остается постоянным, равным напряжению на нагрузке. Это соответствует режиму бегущей волны в линии.
Во втором случае (W / Rн<1) анализ соотношения (1.25) показывает, что максимумы напряжения Umax определяются из условий sin2(bzmax) = 0; cos2(bzmax) = l, где zmax – продольные координаты максимумов напряжения zmax = nlл / 2, п = 0,1,2,... При этом напряжение в максимуме определяется равенством Umax = Uн. Отсюда следует, что на нагрузке линии образуется максимум напряжения. Минимумы напряжения определяются из условий sin2 (bzmin) = 1, cos2 (bzmin) = 0, где zmin – продольные координаты минимумов напряжения: zmin = lл / 4 + nlл / 2, n = 0,1,2,... При этом напряжение в минимуме определяется уравнением Umin = UнW / Rн. Таким образом, при Rн > W Kсв = Umax / Umin = Rн / W.
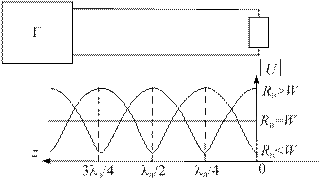
Рис. 1.18.Эпюры напряжения в линии,работающей на активное сопротивление
Рассуждая аналогично применительно к третьему случаю, можно показать, что при Rн < W в конце линии устанавливается минимум напряжения, и zmin = nlл / 2, n = 0,l,2,...,Umin =Uн.При этом координаты напряжения определяются равенством zmax = lл / 4 + nlл / 2, п = 0,1,2,..., а значение напряжения в максимумах Umax= UнW / Rн. В этом случае Kсв = W / Rн. На рис. 1.18 представлены эпюры напряжения в линии для всех трех рассмотренных случаев. Из графиков следует, что при работе линии на активное сопротивление в ней устанавливается режим смешанных волн, за исключением случая Rн = W,при котором устанавливается режим бегущей волны, и вся мощность выделяется в нагрузке.
Определим входное сопротивление линии, нагруженной на активное сопротивление, используя выражение для напряжения и тока (1.24):
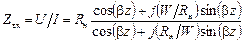
Выделяя здесь действительную и мнимую части, находим:
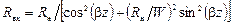 ;
;
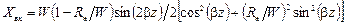 . (1.26)
. (1.26)
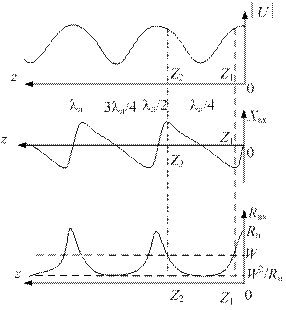
Рис. 1.19. Эпюры напряжения и входного сопротивления в линии нагруженной на активное сопротивление
Зависимости Rвх и Xвх от z для случая Rн> W приведены на рис. 1.19. Здесь же представлена соответствующая эпюра напряжения. Из эпюр следует, что при увеличении сопротивления нагрузки они приближаются к эпюрам, соответствующим линии, разомкнутой на конце. Следует обратить внимание на поперечные сечения линии z1 и z2, в которых активная часть входного сопротивления линии равна волновому сопротивлению W. а реактивная часть имеет емкостный в точке z, или индуктивный в точке z2 характер. Поперечные сечения линии с такими входными сопротивлениями периодически повторяются через lл / 2. Из эпюр также следует, что в сечениях линии, в которых напряжение достигает максимума или минимума, входное сопротивление чисто активное. Это остается справедливым и для случая Rн< W.
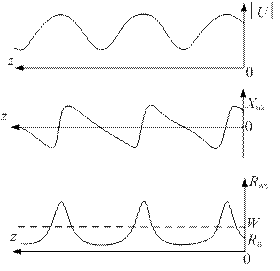
Рис. 1.20. Эпюры напряжения и входного сопротивления в линии, нагруженной на комплексное сопротивление
Работа линии на произвольное комплексное сопротивление. В этом случае, как и при активной нагрузке, часть мощности падающей волны поглощается активной частью нагрузки, и в линии устанавливается режим смешанных волн. Отличие от случая активной нагрузки состоит в фазовом сдвиге, который приобретает отраженная волна в месте включения нагрузки. Этот фазовый сдвиг вызывает сдвиг кривых напряжения и тока без изменения их формы. Для иллюстрации на рис. 1.20 показаны эпюры напряжения и входного сопротивления в линии, нагруженной на комплексное сопротивление, причем реактивная часть этого сопротивления имеет индуктивный характер.
Как и в случае чисто активной нагрузки, в сечениях линии, где напряжение достигает максимума или минимума, входное сопротивление линии чисто активное. Можно показать, что произведение входных сопротивлений, отстоящих один от другого на lл / 4, равно квадрату волнового сопротивления:
Zвх(z)Zвх(z + lл / 4) = W2.
Так как напряжение и ток на произвольной комплексной нагрузке связаны соотношением Uн = IнZн, то из (1.21) можно получить уравнение, определяющее коэффициент отражения через сопротивление нагрузки:
G = (Zн - W) / (Zн + W).
Основные результаты теории линии без потерь.Перечислим основные результаты теории длинных линий без потерь:
1. Напряжение, ток и входное сопротивление являются периодическими функциями относительно продольной координаты с периодом lл / 2, т.е. для любого сечения линии z справедливы равенства:
U(z) =U(z + lл / 2);
I(z) =I(z + lл / 2);
Zвх(z) = Zвх(z + lл / 2). (1.27)
2. Режим стоячих волн в линии реализуется при реактивных нагрузках: холостой ход, короткое замыкание, емкость С,индуктивность L.
3. Режим бегущей волны реализуется чисто активной нагрузкой, равной волновому сопротивлению линии: Rн = W, Хн = 0.
4. Режим смешанных волн реализуется остальными нагрузками, кроме перечисленных в пп. 2 и 3.
5. В сечениях линии, в которых напряжение или ток достигают максимума или минимума, входное сопротивление линии чисто активное.
6. Отрезок линии можно рассматривать как трансформатор сопротивлений, при этом, учитывая (1.27), полуволновый отрезок линии имеет коэффициент трансформации, равный единице, а для произвольного сечения z линии справедливо соотношение:
Zвх(z)Zвх(z + lл / 4) = W. (1.28)
Свойства линии с потерями.Найдем коэффициент распространения k в линии при наличии тепловых потерь в проводах и диэлектрике:
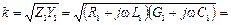
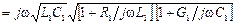 .
.
Принимая во внимание, что потери в реальной линии малы, а круговая частота w велика, можно сделать вывод о малости величин 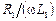 и
и 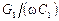 :
: 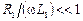 ,
, 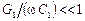 .
.
Разложив в последнем выражении корень в степенной ряд относительно 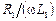 и
и 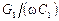 и ограничившись первыми двумя членами в этих разложениях, получим:
и ограничившись первыми двумя членами в этих разложениях, получим:
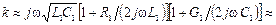
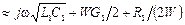 .
.
Так как k = a+ jb, из последнего соотношения найдем:
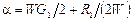 ;
; 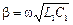 (1.29)
(1.29)
В практических случаях потери в диэлектрике пренебрежимо малы по сравнению с потерями в металле, поэтому в (1.29) выражение для aможно упростить:
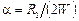 . (1.30)
. (1.30)
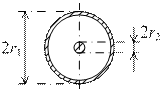
В табл. 1.3 приведены формулы для вычисления основных параметров двухпроводной и коаксиальной линий, выполненных из меди.
Таблица 1.3
| Параметр | 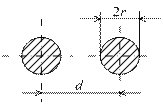
| 
|
| С1, пФ/м | 12,1erlg(d / r) | 24,1er / lg(r1 / r2) |
| L1, мкГн/м | 0,92lg(d / r) | 0,46 lg(r1 / r2) |
| R1, Ом/м | 1,44 / 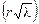
| 0,72(1 / r1 + 1 / r2) / 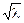
|
| W, Ом | 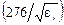 lg(d / r) lg(d / r)
| 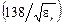 lg(r1 / r2) lg(r1 / r2)
|
Примечание: er – относительная диэлектрическая проницаемость диэлектрика: в формулах для R1, l – в метрах, r, r1, r2 – в миллиметрах.
Коэффициент полезного действия линии.Важным параметром линии с потерями является ее коэффициент полезного действия (КПД). Определим КПД как отношение мощности Рн, выделившейся в нагрузке, к мощности Рп, подведенной к линии:
h = Pн / Рп. (1.31)
Примем длину линии, равной l. Найдем КПД линии, работающей в режимах бегущей волны и смешанных волн. В первом случае, в соответствии с (1.6). выражения для напряжения и тока примут вид:
U = AUekz, I = АIekz. (1.32)
Мощность, выделяющуюся в нагрузке, найдем из соотношения
Pн = 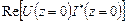 . (1.33)
. (1.33)
Здесь символ Re обозначает выделение действительной части из выражения, находящегося в квадратных скобках, а звездочка над буквой - операцию комплексного сопряжения.
Подставляя в выражение для Рн значения напряжения и тока из (1.32), получаем:
Рн=АU А*I.
Найдем мощность, подводимую к линии длиной l:
Pн = 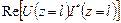 . (1.34)
. (1.34)
Откуда, с учетом (1.32), определим
Рп = АU А*Ie2kl.
Подставляя найденные значения Рни Рпв (1.31), получаем:
h = e2kl. (1.35)
Если потери малы, т.е. al << 1, то последняя формула упрощается, если экспоненту представить в виде ряда по степеням аргумента -2al и ограничиться в этом ряду первыми двумя членами: h » 1 - 2al.
В режиме смешанных волн будем использовать выражение для напряжения и тока в виде (1.6), которые с учетом (1.12) примут вид:
U = AUekz + BUe-kz = AU(ekz + G e-kz);
I =(1 / W) AUekz + BUe-kz = (AU / W)(ekz + G e-kz). (1.36)
Для определения КПД найдем Рни Рп,используя (1.33) и (1.34):
Pн=(АU А*U / W)(1 - çGç2); (1.37)
Pп=(АU А*U / W)(1 - çGç2е-4al). (1.38)
Выражение для мощности, выделяющейся в нагрузке (1.37), имеет весьма характерный вид. Первое слагаемое в этом выражении представляет собой мощность падающей волны в месте подключения нагрузки (z = 0). Второе слагаемое есть мощность, уносимая отраженной волной в этом же сечении. Их разность определяет мощность, поглощаемую в нагрузке. Таким образом, выражение для КПД в режиме смешанных волн примет вид:
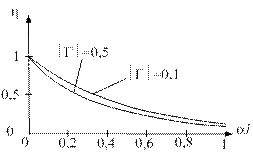
Рис. 1.21. Зависимость КПД линии от потерь при различном ее согласовании
h = Pн/ Pп= (1 - çGç2)е-2al / (1 - çGç2е-4al). (1.39)
Зависимость КПД от al проиллюстрирована графически на рис. 1.21. Из графиков следует, что если потери малы, то КПД слабо зависит от модуля коэффициента отражения. Если же потери значительны, то КПД сушественно зависит от степени согласования линии с нагрузкой.
Следует отметить, что формула (1.39)получена в предположении, что генератор не согласован с линией, т.е. отраженная от нагрузки волна, достигая источника, полностью от него отражается и вновь направляется в нагрузку. Если же отраженная волна поглощается в генераторе, то
h = (1 - çGç2)е-2al.
Из сравнения этого выражения с (1.39)следует, что КПД линии при несогласованном генераторе выше, чем для согласованного.
Дата добавления: 2020-07-18; просмотров: 666;











