Способы широкополосного согласования

На практике применяются сочленения и элементы тракта, предназначенные для работы в полосе частот 10% и более. Такую полосу частот принято называть широкой, а устройства, работающие в такой полосе, – широкополосными. В технических требованиях к этим устройствам указывается полоса частот (см. рис. 2.1) идопустимое рассогласование, K_св < K_св.доп этой полосе. Задача широкополосного согласования возникает, например, при необходимости стыковки линий передачи с различными размерами или формами поперечных сечений, а также при работе тракта с широкополосными сигналами, например, линейно-частотномодулированными или шумоподобными.

Основными широкополосными согласующими устройствами являются:

• широкополосные частотные компенсаторы;

• ступенчатые трансформаторы;

• плавные переходы или неоднородные линии.

Рассмотрим принцип работы каждого из этих устройств.

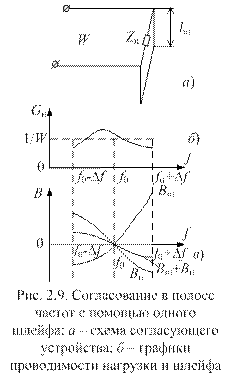
Принцип частотной компенсациисостоит во взаимной компенсации частотных изменений сопротивления нагрузки и согласующих элементов. Его можно осуществить за счет подбора необходимого закона частотного изменения сопротивления согласующих элементов. Рассмотрим широкополосное согласование комплексных сопротивлений с помощью одного шлейфа (рис. 2.9, а).Предположим, что график проводимости согласуемой нагрузки Y_н = 1/Z_н = G_н + jВ_нимеет вид, изображенный на рис. 2.9, б.На этом же рисунке представлен график входной реактивной проводимости согласующего шлейфа В_ш,(рис. 2.9, в), включенного по схеме рис. 2.9, а. Наклон кривой В_ш подобран примерно равным наклону кривой В_н с обратным знаком. Поэтому суммарная реактивная проводимость В_н+ В_шуменьшается и меньше изменяется с частотой, чем реактивная проводимость нагрузки. В соответствии с (1.23) входное сопротивление короткозамкнутого шлейфа определяется соотношением

Z_вх(z_ш) = jX_ш = jW_шtg(bl_ш).

Найдем входную проводимость этого шлейфа:

Y_вх.ш = 1/Z_вх.ш = jB_ш = (-j/W_ш)сtg(bl_ш).

Учитывая, что b = w/n_ф =2pf/n_ф, получаем:

B_ш = (-1/W) сtg(2pfl_ш/n_ф).

Таким образом, подбором величины волнового сопротивления шлейфа и его длины можно изменять наклон кривой В_ши полосу частот, в которой реактивная проводимость изменяется в допустимых пределах.

Активная составляющая проводимости нагрузки при необходимости может быть согласована с помощью четвертьволнового трансформатора.

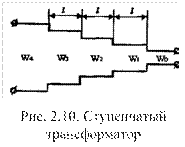Ступенчатые трансформаторы применяются для согласования линии с активной нагрузкой или нагрузкой, имеющей небольшую реактивную составляющую. Например, согласование при сочленении двух линий передачи с различными волновыми сопротивлениями достигается с помощью промежуточного нерегулярного отрезка линии, называемого трансформатором или переходом. Ступенчатые трансформаторы представляют собой каскадное включение отрезков линий передачи с различными волновыми сопротивлениями (рис. 2.10.), но имеющими одинаковую длину l. Волновые сопротивления соседних ступенек отличаются на небольшую величину, и отражения от них невелики. Принцип работы ступенчатого трансформатора заключается в том, что всегда найдется хотя бы пара ступенек, отражение от которых компенсируется. Чем больше ступенек, тем лучше согласование и шире полоса пропускания. Структура трансформатора определяется числом ступенек п. Рис. 2.10. Ступенчатый длиной ступеньки l и отношением трансформатор волновых сопротивлений соседних ступенек. Свойства трансформатора описываются его частотной характеристикой, которая представляет собой зависимость рабочего затухания L от частоты. Под рабочим затуханием понимают величину:

L = P_вх/P_выхили L = 10lg(P_вх/P_вых) [дБ],

где Р_вх, Р_вых – мощность на входе и выходе трансформатора соответственно. Затухание в трансформаторе определяется отражениями от его входа в полосе частот. При этом в качестве аргумента функции рабочего затухания L берут величину q = 2pl/l = 2pl/c, где с скорость света в вакууме. Поэтому частотная характеристика трансформатора представляет собой зависимость рабочего затухания L от электрической длины ступеньки.

Определение структуры трансформатора по заданным полосе частот 2Df и допустимому рассогласованию K_св.доп является задачей синтеза согласующего устройства. Решение этой задачи рассмотрено, например, в монографии Кац Б.М. и др. "Оптимальный синтез устройств СВЧ с Т-волнами" / Под ред. В. П. Мещанова. – М.: Радио и связь, 1984. – 288 с.

Наибольшее распространение на практике имеют трансформаторы с частотными характеристиками двух типов: 1) чебышевская характеристика; 2) максимально плоская характеристика. Чебышевская характеристика описывается полиномами Чебышева и имеет вид:

L = l + h²T_n²(tcosq),

где h, l– масштабные коэффициенты; Т_n – полином Чебышева первого рода n-го порядка; n – число ступенек трансформатора. Типичный график чебышевской характеристики при n = 3 представлен на рис. 2.11, a, где b_п – затухание в полосе пропускания 2Dq_п, b₃ – затухание в полосе заграждения 2Dq_з. Характерным для чебышевских характеристик является наличие равноамплитудных осцилляции, число которых n + 1 на единицу превышает число ступенек трансформатора.

Максимально плоская характеристика описывается функцией вида

L = l + h²(tcosq)²ⁿ.

График максимально плоской характеристики показан на рис. 2.11, б. Следует отметить, что основное отличие трансформаторов с чебышевской и максимально плоской характеристиками состоит в том, что при одинаковых параметрах перехода (b_п, b_з) трансформатор с максимально плоской характеристикой имеет большую длину, но более линейную фазочастотную характеристику.

Из выражений, определяющих функции рабочего затухания L, следует, что относительно аргумента q они периодические с периодом p. Практически используется лишь первый период функции, для которого длины ступенек получаются наименьшими.

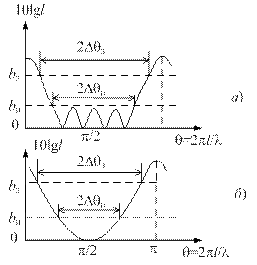Рис. 2.11. Частотные характеристики ступенчатых трансформаторов: а – чебышевская, б – максимально плоская

Плавные переходыиспользуются также для согласования активных нагрузок и могут рассматриваться как предельный случай ступенчатого перехода при увеличении числа ступенек п до бесконечности и неизменной длине перехода. Частотные характеристики плавных переходов непериодические. Наиболее часто употребляются на практике экспоненциальный переход, чебышевский переход и вероятностный переход, являющийся предельным случаем ступенчатого перехода с максимально плоской характеристикой.

Плавный переход, по существу, является нерегулярной двухпроводной линией передачи, в которой погонные параметры и волновое сопротивление – функции продольной координаты. При этом эквивалентная схема элементарного участка такой линии длиной dz имеет вид, как и для регулярной линии (см. рис. 1.10). Поэтому остаются справедливыми телеграфные уравнения (1.2). Все входящие в эти уравнения величины зависят от z. В частности, для двухпроводной экспоненциальной линии (рис. 2.12) при увеличении z растет |Z₁|, а |Y₁| уменьшается.

Это обусловлено увеличением погонной индуктивности L₁ и уменьшением погонной емкости С₁ вызванными увеличением расстояния между проводами. Можно подобрать геометрию линии так, чтобы оставалась постоянной вдоль линии величина k = 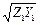. Можно показать, что волновое сопротивление в такой линии изменяется по экспоненциальному закону:

W = W₀e^bz, b ¹ 0,

где W₀ – волновое сопротивление в начале линии; b – коэффициент, определяющий скорость изменения волнового сопротивления вдоль линии. Подбирая значения W₀и b, можно обеспечить широкополосное согласование. Эффективность согласования зависит от скорости изменения волнового сопротивления вдоль линии. Чем медленнее изменяется W, тем шире полоса согласования и больше длина перехода.

Недостатком плавных экспоненциальных переходов является их большая длина при значительных перепадах волнового сопротивления. Например, при W(z=l) /W₀ = е^bl = 7,4 и допуске на рассогласование |Г_max| £ 0,05 длина перехода l ³ 3l. При этом длина оптимального че-бышевского перехода в 3¸4 раза меньше. Среди плавных переходов при одинаковых перепадах волновых сопротивлений, нижней граничной частоте и допуске на рассогласование наименьшую длину имеют чебышевские переходы.

Сравнение ступенчатых и плавных переходов показывает, что при одинаковых параметрах длина ступенчатого перехода заметно меньше, чем плавного. Однако при этом полоса пропускания плавного перехода гораздо шире. При повышенных требованиях к электрической точности плавный переход предпочтительнее ступенчатого. Снижение электрической прочности последнего объясняется концентрацией электромагнитного поля в местах стыков отдельных ступенек. Следует отметить, что существует теоретическое ограничение на ширину полосы согласования, которое устанавливается теоремой Фано:

2Df/f = p/(Q ln|Г|),

где Q – добротность нагрузки, определяемая как отношение реактивной мощности, накапливаемой в нагрузке на средней частоте f₀, к мощности тепловых потерь. Согласование невозможно также на частотах, соответствующих бесконечно большим реактивным сопротивлениям или проводимостям нагрузки.