Располагаемая работа

При истечении газа

Величина 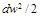, равная бесконечно малому приращению внешней кинетической энергии рабочего тела, называется элементарной располагаемой работой. Эта энергия может быть использована для получения внешней полезной работы.

Из сравнения уравнений (4.8) и (10.6) следует, что для обратимого процесса течения газа

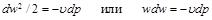. (10.10)

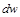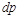Равенство (10.10) показывает, что при движении рабочего тела по каналу знаки и противоположны. Если 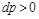, то газ сжимается и его скорость уменьшается: .

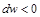Если 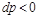, то газ расширяется и его скорость увеличивается: .

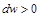Эта закономерность лежит в основе специальных каналов переменного сечения, называемых соплами и диффузорами.

Если при перемещении газа по каналу происходит его расширение с уменьшением давления и увеличением скорости, то такой канал называется соплом.

Если в канале происходит сжатие рабочего тела с увеличением его давления и уменьшением скорости, то такой канал называется диффузором.

Располагаемую работу при истечении газа можно представить графически на 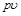-диаграмме. На рис. 10.1 изображен обратимый процесс расширения газа 1-2.

Бесконечно малая располагаемая работа – 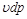измеряется элементарной площадкой 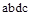. Очевидно, вся располагаемая работа в процессе 1–2 равна

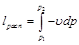. (10.11)

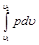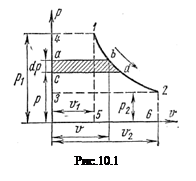
Приращение кинетической энергии потока газа (располагаемая работа), как это следует из (4.8) и (10.6) представляет собой разность работ расширения потока газа и работы проталкивания 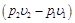. Располагаемая работа l_расп измеряется пл. 1234, ограниченной линией процесса расширения газа, абсциссами крайних точек и осью ординат .

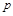Если кривая 1–2 является политропой, то располагаемую работу определяем из уравнения

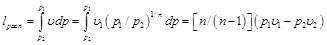(10.12)

При адиабатном расширении идеального газа

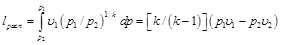. (10.13)

Сравнивая располагаемую работу при истечении (пл. 1234) с работой расширения газа (пл.1265), получаем, что величина располагаемой работы в n раз больше работы расширения газа:

.

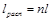Из уравнения (10.4) следует, что

.

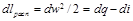или

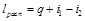. (10.14)

Располагаемая работа при течении газа может быть получена за счет внешней теплоты и уменьшения энтальпии газа. Это уравнение справедливо как для обратимых, так и для необратимых процессов течения газа с трением.

При адиабатном течении из уравнения (10.14)

,

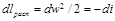откуда

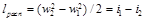. (10.15)

Из уравнения (10-15), принимая w₁≈0 найдём скорость истечения

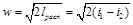. (10.16)