ДРОССЕЛИРОВАНИЕ ГАЗОВ И ПАРОВ

Если на пути движения потока газа или пара имеется резкое су­жение сечения (не полностью открытый вентиль или кран, перегородка с небольшим отверстием, как показано на рис. 11.1, и др.), которое создает местное сопротивление потоку, то в месте сужения сечения скорость движения потока резко возрастает, а давление падает. За сужением скорость уменьшается и восстанавливается до первоначаль­ной, но давление из-за потерь на завихрение восстанавливается не полностью.

Рис. 11.1. Дросселирование газа или пара при течении в канале с диафрагмой

Явление понижения давления потока в результате его прохожде­ния через местное сопротивление называется дросселированием.

При отсутствии теплообмена и в случае, если поток не совершает техническую работу, для горизонтального потока выражение первого закона термодинамики (10.5) примет вид

или

(11.1)

где i₁ и i₂ – значения энтальпии в се­чениях I и II, удаленных от местного сопротивления. Так как в процессе дросселирования изменение скорости очень мало и им можно пренебречь, то выражение (11.1) примет вид

i₁= i₂, (11.2)

т. е. при дросселировании газа или пара энтальпия не изменяется.

Учитывая, что для идеального га­за i₂ – i₁ = с_рт (t₂ – t₁), то из (11.2) следует t₁= t₂ т.е. при дросселиро­вании идеального газа его температу­ра не изменяется.

При дросселировании реального газа температура его может умень­шаться, увеличиваться или оставаться неизменной. Если температура реального газа в результате дросселирования остается без изменения, то она называется температурой инверсии Т_инв.

Таким образом, поведение реальных газов при дросселировании существенно отличается от поведения идеальных газов. Изменение температуры реальных газов при дросселировании впервые было об­наружено опытами Джоуля и Томсона и получило название эффекта Джоуля — Томсона.

С молекулярной течки зрения эффект Джоуля — Томсона объяс­няется наличием объема самих молекул и сил сцепления между моле­кулами реального газа. Влияние объема молекул и сил взаимодей­ствия на изменение температуры в процессе дросселирования различно в зависимости от природы газа и начального состояния реального газа.

Для каждого газа существует определенная температура инверсии, которая приблизительно равна

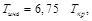(11.3)

где Т_кр — критическая температура газа, °К.

Температура инверсии большинства газов, за исключением водо­рода и гелия, достаточно велика и процессы дросселирования обычно протекают с уменьшением температуры. Поскольку процесс дроссели­рования сопровождается трением и завихрением, он является необра­тимым и поэтому не может быть изображен каким-либо графиком.

Задачи, связанные с дросселированием водяного пара, проще всего решаются при помощи i – s – диаграммы. Из основного условия дросселирования (i₁= i₂) конечное состояние пара определяется пересече­нием горизонтали, проходящей через начальную точку (рис. 11.2), с изобарой конечного давления р₂.

Рис. 11.2. Условное изо­бражение процесса дрос­селирования пара на i – s - диаграмме

Из диаграммы видно, что температура водяного пара в про­цессе дросселирования уменьшается. При этом влажный насыщен­ный пар в зависимости от величины на­чального давления, степени сухости и ко­нечного давления может быть после дрос­селирования влажным (а — b), сухим на­сыщенным (а — с) или даже перегретым

На рис. 11.3 представлены процессы расширения водяного пара в двигателе до (процесс 1-3) и после дросселирования (линия 2-4). Поскольку , то работоспособность газа или пара в результате дросселирования уменьшается.

Рис. 11.3

Несмотря на то, что дросселирование яв­ляется необратимым процессом и сопровож­дается потерей работоспособности потока, в силу простоты конструкции и эксплуатации дроссельных устройств явление дросселирова­ния широко используется в технике для ре­гулирования и измерения расходов и получе­ния низких температур.

КОМПРЕССОРЫ

Для получения сжатых газов и паров применяются машины, на­зываемые компрессорами. По рабочему процессу и конструктивному оформлению компрессоры делятся на поршневые, центробежные, осе­вые и пароструйные. Несмотря на эти различия, термодинамические основы нагнетания общие для всех типов. Поэтому рассмотрим ра­бочий процесс поршневых компрессоров, которые получили наиболь­шее распространение в промышленности.

Схема компрессора и теоретическая индикаторная диаграмма показаны на рис. 12.1. Здесь 1 – цилиндр, внутри которого пере­мещается поршень 2, совершающий возвратно-поступательное движе­ние.

Рис. 12.1. Схема одноступенчатого компрессора и теоретические процессы на р – υ–(a), T – s –(б) и i – s–диаграммах (в)

Индикаторная диаграмма изображает зависимость давления газа в цилиндре от его объема. Линия р₁21р₂ характеризует процесс вса­сывания, который осуществляется при движении поршня вправо при открытом всасывающем клапане 4. Процесс сжатия, происходящий при движении поршня влево, в зависимости от количества отводимой теплоты от воздуха при его сжатии может быть изотермным (1 –2), адиабатным (1 –2') или политропным (1 –2").

Отвод теплоты от сжимаемого газа осуществляется водой, цирку­лирующей в рубашке цилиндра 5, образуемой полыми стенками ци­линдра. Линия 2 – р₁ изображает процесс нагнетания через открытый нагнетательный клапан 3 (выталкивания газа в какой-либо резер­вуар при неизменных р, υ и Т), который происходит при достижении давления р₂.

Вследствие того, что параметры газа в процессах р₂ – 1 и 2 – р₁ не меняются, а меняется только его количество, эти процессы не яв­ляются термодинамическими.

С начала нового хода поршня открывается всасывающий клапан 4, давление в цилиндре снижается от р₂ до р₁ теоретически мгновен­но, т. е. по вертикали p_l – p₂, и процесс повторяется.

В задачу термодинамического анализа сжатия газа в компрессо­рах входит определение работы, которую необходимо затратить на получение сжатого газа, и мощности приводного двигателя.

Общее выражение для работы, затрачиваемой на нагнетание l_н, может быть получено из аналитического выражения первого закона термодинамики для потока (10.6), которое с учетом знаков работы (l_т=–l_н) и теплоты (q = – q_охл) и пренебрежения изменением по­тенциальной энергии потока запишется так:

Отсюда

(12.1)

Выражение (12.1) является основным уравнением термодинамики нагнетания. С другой стороны, при принятых допущениях из выраже­ния (10.11) следует

Для случая политропного сжатия, согласно (10.12), работа на­гнетания

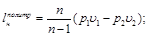(12.2)

для случая адиабатного сжатия

(12.3)

для изотермного сжатия (pυ = const) υdp = – pdυ и

(12.4)

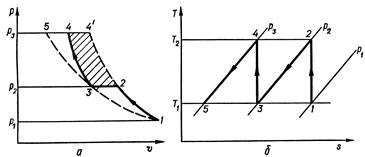
Рис. 12.2. Графики процесса сжатия в двухступенчатом компрессоре в р – v–(a) и Т– s– координатах (б)

Если учесть, что разница скоростей на входе и на выходе из ком­прессора небольшая w₁ ≈ w₂, то выражение (12.1) примет вид

l_н = i₂ - i₁ + q_охл, (12.5)

для адиабатного сжатия (q_охл = 0)

(12.6)

где i₁ и i₂ – соответственно начальное и конечное значения энтальпии (рис.12.1, в). Теоретическая мощность, необходимая для привода компрессора:

N = ml_н квт, (12.7)

где т — массовый расход, кг/сек.

Наименьшая работа в компрессоре, как это видно из рис.12.2, а, затрачивается при изотермическом сжатии, но для этого требуется большой расход охлаждающей воды. Процесс сжатия воздуха чаще всего протекает по политропе с показателем n = 1,2÷1,25. При сжа­тии воздуха без охлаждения показатель политропы n = k и сжатие воздуха произойдёт по адиабате (рис. 12.1, а).

В одноступенчатом компрессоре степень повышения давления ограничивается допустимой температурой воздуха, с повышением кото­рой ухудшаются условия смазки. Для получения сжатого газа более высокого давления (более 1–1,2 Мnа) применяются многоступенча­тые компрессоры с промежуточным охлаждением газа после каждой ступени. Этим также достигается приближение процесса к изотерми­ческому и более экономичная работа компрессора. Обычно здесь стремятся к тому, чтобы газ после промежуточного холодильника имел ту же температуру, при которой он поступил в предыдущую ступень. Специальные расчеты показывают, что наиболее выгодным оказывается многоступенчатое сжатие в том случае, когда отношение давлений в каждой ступени принимается одинаковым для всех сту­пеней.

На рис. 12.2 приведены р – υ – и Т – s – диаграммы двухступенчатого компрессора. Здесь линии 1 – 2 и 3 – 4 – процессы адиабатного сжа­тия в ступенях компрессора, а линии 2 – 3 и 4 – 5 – процессы охлаж­дения газа в промежуточных холодильниках при р = const.

Заштрихованная площадь 2344 на рис.12.2, а иллюстрирует экономию в затрате энергии на сжатие во второй ступени благодаря промежуточному охлаждению.

Выше была рассмотрена работа идеального одноступенчатого порш­невого компрессора. В действительности надо считаться с тем, что кон­структивно компрессор приходится осуществлять так, чтобы поршень не доходил до крайнего торца цилиндра, где размещают крышку со впускным и выпускным клапанами. Объем между торцом крышки цилиндра и крайним положением поршня называют вредным простран­ством. Его наличие, а также влияние работы клапанов, сопротивления при всасывании и выталкивании и утечки воздуха влияют на работу и производительность реального компрессора и заставляют вносить коррективы в выведенные выше формулы.