Классификация контрольных карт Шухарта

Выделяют два вида контрольных карт Шухарта:

1 Контрольные карты, для которых не заданы стандартные значения. Стандартные значения – значения, априорно установленные в соответствии с некоторыми конкретными требованиями или целями. Цель таких карт – обнаружение отклонений значений статистических характеристик, которые вызваны неслучайными причинами.

2 Контрольные карты, для которых заданы стандартные значения. Цель таких карт – определение того, отличаются ли наблюдаемые значения характеристик процесса (например, ) от соответствующих стандартных значений (например, X₀) больше, чем можно ожидать при действии только случайных причин. Стандартные значения могут быть основаны на опыте, полученном при анализе аналогичных технологических процессов, на экономических показателях или указаны в технических требованиях на продукцию.

В настоящих курсе далее рассматриваются только контрольные карты, для которых не заданы стандартные значения.

Выделяют статистический контроль по количественному и качественному (альтернативному) признакам.

Контроль качества продукции, в процессе которого определяют значения одного или нескольких количественных показателей качества (например, сопротивление в омах, шум в децибелах и т.д.), а последующее решение о контролируемой совокупности принимают в зависимости от этих значений, называется контролем по количественному признаку.

Контроль качества продукции, в ходе которого каждую проверенную её единицу относят к определенной группе, а последующее решение о контролируемой совокупности принимают в зависимости от соотношения количеств её единиц, оказавшихся в разных группах, называется контролем по качественному признаку.

Контроль по альтернативному признаку является частным случаем контроля по качественному, когда совокупность продукции состоит из двух групп: годной и дефектной (соответствующей и несоответствующей) продукции. Решение о контролируемой совокупности принимается в зависимости от числа обнаруженных дефектных единиц или числа дефектов, приходящихся на определенное число единиц продукции.

В соответствии с этим контрольные карты Шухарта также разделяют на два типа: карты контроля по количественному признаку и карты контроля по качественному либо альтернативному признаку.

Примерами контрольных карт по количественному признаку являются:

- карты среднего ( ) и размахов (R);

- карты индивидуальных значений (X) и скользящих размахов (R);

- карты медиан (Me) и размахов (R).

Примеры и остальные сведения о картах контроля по качественному и альтернативному признакам рассмотрим на следующей лекции.

Для контрольных карт, использующих количественные данные, предполагается нормальное (гауссово) распределение значений внутри выборок. Поскольку контрольные границы используются только как эмпирические критерии при принятии решений, целесообразно пренебрегать малыми отклонениями от нормальности.

В этой и следующей лекциях рассматриваются только карты средних арифметических ( ), размахов (R) и долей несоответствующих единиц продукции (p). Эти карты являются самыми распространенными.

Для анализа и управления процессом по количественному признаку совместно используются карты средних арифметических ( ) и размахов (R). Полученное сочетание называют -R-картой. В случае использования альтернативных данных достаточно применения только карты долей несоответствующих единиц продукции (p).

Не смотря на то, что получение количественных данных дороже, чем альтернативных, объемы выборок для количественных данных почти всегда значительно меньше. Это позволяет в некоторых случаях снизить общую стоимость контроля и уменьшить временной разрыв между производством продукции и корректирующим воздействием. Так, для построения -R-карты в большинстве случаев достаточно 20…25 выборок, объемом 4…5. При построении p-карты при том же количестве выборок объем выборки должен быть таким, чтобы для предполагаемой доли несоответствующей продукции среднее количество обнаруживаемых несоответствующих единиц продукции в выборке было не менее пяти. Например, если требуется следить за процессом с долей несоответствующей продукции порядка 1%, то нужны выборки объемом не менее 500 изделий.

Нет общих правил для выбора частоты отбора выборок и их объемов. Частота может зависеть от стоимости процедур взятия и анализа выборки, а объем подгрупп – от ряда практических соображений. Например, большие выборки, берущиеся с меньшей частотой, могут обнаружить малый сдвиг среднего процесса более точно, но малые выборки, берущиеся чаще, обнаруживают большие сдвиги быстрее. Часто объем выборки берется равным 4 или 5 единиц, а частота отбора обычно выше в начале работы, чем при достижении состояния статистической управляемости. Обычно 20...25 подгрупп объема 4 или 5 рассматриваются как приемлемые для получения предварительных оценок.

1.3 Карта средних арифметических и размахов ( -R-карта)

В таблицах 6 и 7 приведены формулы контрольных границ и коэффициенты для -R-карт [2,3].

Таблица 6 – Формулы контрольных границ -R-карт

Статистика	Центральная линия (CL)	Контрольные границы (LCL и UCL)
LCL	UCL
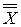
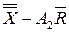
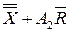
R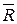

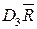
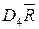
Таблица 7 – Коэффициенты -R-карт

Объем выборки, n	Коэффициенты -R-карт
A2	D3	D4	1/d2
	1,880	0,000	3,267	0,8865
	1,023	0,000	2,574	0,5907
	0,729	0,000	2,282	0,4857
	0,577	0,000	2,114	0,4299
	0,483	0,000	2,004	0,3946
	0,419	0,076	1,924	0,3698
	0,373	0,136	1,864	0,3512
	0,337	0,184	1,816	0,3367
	0,308	0,223	1,777	0,3249

Система карт Шухарта опирается на следующее условие: если изменчивость процесса от единицы к единице и среднее процесса остаются постоянными на данных уровнях (оцененные, соответственно, по 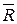и 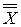), то размахи R и средние отдельных подгрупп будут меняться только случайным образом и редко выходить за контрольные границы. Не допускаются очевидные тренды или необычные структуры данных.

Последовательность построения и использования -R-карты:

1 Собирают и анализируют данные, вычисляют средние и размахи.

2 Строят R-карту. Сопоставляют нанесенные точки размахов с контрольными границами, выделяют точки вне границ, необычные структуры или тренды, например непрерывный рост размахов в течение ряда выборок. Для каждого сигнала о наличии неслучайной причины в значениях размаха проводят анализ операций процесса, чтобы определить причину. Проводят корректирующие действия и действия по предотвращению повторения данной причины.

3 Исключают все подгруппы, на которые повлияла особая причина, затем пересчитывают и наносят на карту новые средний размах 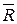и контрольные границы. Пункты 2 и 3 повторяют, пока последняя из построенных диаграмм не укажет на статистическую управляемость. Выборки, исключенные из R-карты из-за выявленных особых причин, надо исключить и из -карты.

4 Строят -карту и сравнивают ее точки с контрольными границами. Выделяют точки вне границ, необычные структуры точек или тренды. Для -карты существует ряд критериев, позволяющих выявлять неслучайные причины [3,4]. Таковыми, например, являются:

- девять точек подряд по одну сторону от центральной линии;

- шесть возрастающих или убывающих точек подряд;

- четырнадцать попеременно возрастающих и убывающих точек.

Эти критерии следует рассматривать только как примеры ситуаций, когда может быть установлено проявление неслучайных причин. Следует обращать внимание на любое необычное расположение точек. Далее, также как и для R-карты проводят корректирующие действия. Точки (выборки), для которых были найдены неслучайные причины, исключают. Выборки, исключенные из -карты из-за выявленных особых причин, надо исключить и из R-карты. Повторно вычисляют и наносят на график новое среднее процесса ( ) и контрольные границы. Пункт 4 повторяют, пока последняя из построенных диаграмм не укажет на статистическую управляемость.

5 При необходимости, после устранения особых причин, пункты 1…5 повторяют. Полученные контрольные границы используют для дальнейшего статистического управления процессом.

При статистическом управлении процессом решается ряд задач:

- обнаружение выхода процесса из статистически управляемого состояния;

- систематическое обнаружение возникающих особых (неслучайных) причин и устранение их;

- настройка процесса;

- определение возможностей процесса, принятие решений по его улучшению.

Возможности процесса определяются его изменчивостью, обусловленной только обычными причинами, т.е. минимальной изменчивостью, которая остается после устранения всех особых причин. Возможности процесса – это показатели самого процесса в статистически управляемом состоянии. Процесс сначала приводят в такое состояние, а затем определяют его возможности. Перед определением возможностей процесса текущие контрольные карты должны демонстрировать сохранение процесса в статистически управляемом состоянии, по крайней мере, для 25 выборок. Далее разброс данных на выходе процесса сравнивается с техническими требованиями для подтверждения того, что эти требования могут быть уверенно выполнены.

Возможности процесса определяют индексом возможностей процесса PCI:

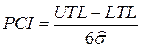, (69)

где: UTL – верхнее предельно допустимое значение контролируемого параметра;

LTL – нижнее предельно допустимое значение контролируемого параметра;

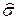– оценка среднеквадратического отклонения внутри выборок.

Существует несколько методов определения 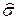. Наиболее простой из них выражается формулой [2]:

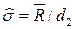. (70)

Величина 1/d₂ приведена в таблице 7.

Индекс возможностей PCI часто применяют для классификации процессов в зависимости от степени соответствия установленным допускам [5]:

- низкая относительная возможность процесса: PCI<1 (трудно обеспечить допуск);

- средняя относительная возможность процесса: PCI <1,33;

- высокая относительная возможность процесса: PCI>1,33 (нетрудно обеспечить допуск).

На практике в качестве минимально приемлемого значения берется .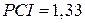

Наряду с индексом возможностей процесса используется величина, обратная ему – коэффициент точности процесса:

. (71)

Если процесс находится в управляемом состоянии и возможности его приемлемы, следует обратить внимание на центр настройки контролируемого параметра, положение которого указано на -карте. Положение центра настройки оценивают с помощью коэффициента настроенности процесса [6]:

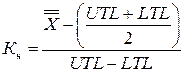. (72)

Чем ближе величина К_н к нулю, тем точнее настроен процесс. В случае обнаружения большого отклонения от эталонного значения следует изменить настройку процесса.

Ключевым параметром, влияющим на принятие решений о воздействии на технологический процесс, является уровень дефектности. Уровень дефектности – доля дефектных единиц продукции или число дефектов на сто единиц продукции. Если рассчитаны К_н и К_т, уровень дефектности может быть определен из номограммы, приведенной на рисунке 18 [6].

Рисунок 18 – Номограмма определения уровня дефектности

Кроме того, для определения доли дефектной продукции можно воспользоваться формулой:

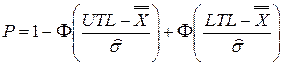, (73)

где 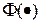– функция нормального распределения случайной величины.

1.4 Пример построения и анализа -R-карты

В таблице 8 приведены результаты измерений сопротивлений 25 выборок резисторов (k=25), объемом 5 штук каждая (n=5). Требуется привести технологический процесс производства резисторов номинальным сопротивлением 1 кОм и максимально допустимой погрешностью ±5% в статистически управляемое состояние, после чего оценить его возможность производить резисторы с указанными параметрами, сделать выводы о необходимости настройки либо модернизации оборудования. Вероятная доля дефектных резисторов не должна превышать 1%.

Найденные средние значения и размахи выборок также занесены в таблицу 8.

Таблица 8 – Данные технологического процесса

Номер выборки	Сопротивление	Среднее ( )	Размах (R)
x1	x2	x3	x4	x5
	0,995	0,999	1,013	1,005	1,001	1,003	0,018
	1,011	0,991	0,983	0,982	1,016	0,996	0,034
	0,990	1,010	1,058	0,985	0,989	1,006	0,073
	1,011	1,013	1,007	1,020	0,983	1,007	0,037
	1,015	0,998	1,017	1,008	1,006	1,009	0,019
	1,007	1,001	0,982	0,987	1,017	0,999	0,035
	1,003	0,988	1,001	1,016	1,005	1,003	0,028
	0,988	1,005	0,986	0,988	0,984	0,990	0,021
	0,982	0,981	1,016	1,017	1,001	1,000	0,036
	0,988	1,017	1,016	0,988	1,009	1,003	0,029
	1,000	1,011	1,004	1,006	0,982	1,001	0,028
	1,004	1,002	1,011	0,980	1,011	1,002	0,031
	1,019	1,004	0,984	1,013	1,015	1,007	0,034
	1,005	1,009	0,990	0,993	1,003	1,000	0,019
	1,018	0,981	0,997	1,017	1,012	1,005	0,036
	1,004	0,996	1,011	1,003	1,010	1,005	0,014
	0,999	0,997	0,982	1,007	1,009	0,999	0,027
	0,990	0,980	1,012	0,987	0,986	0,991	0,031
	0,991	0,983	1,012	1,008	1,005	1,000	0,030
	0,990	0,991	1,008	1,002	0,994	0,997	0,018
	1,009	0,984	0,988	0,999	0,987	0,993	0,024
	0,992	0,993	1,019	1,003	0,983	0,998	0,036
	0,997	0,984	1,016	1,018	1,010	1,005	0,034
	1,001	0,994	1,017	1,003	1,010	1,005	0,022
	0,998	0,984	1,010	1,005	1,012	1,002	0,028

Определим среднее значение размахов выборок.

.

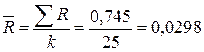Находим координаты центральной линии (CL), верхней (UCL) и нижней (LCL) контрольных границ по формулам, приведенным в таблице 6. Коэффициенты формул приведены в таблице 7.

.

.

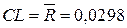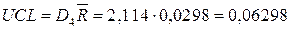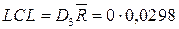(LCL отсутствует).

Строим R-карту (рисунок 19).

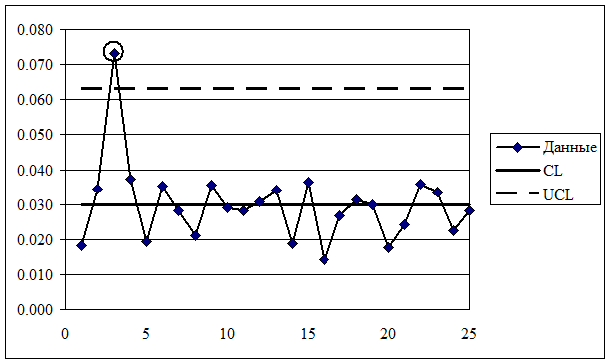
Рисунок 19 – R-карта (оригинальные данные)

Точка, соответствующая выборке номер 3, выходит за UCL, что говорит о том, что процесс находится в статистически неуправляемом состоянии. В момент изготовления резисторов из партии номер 3 на технологический процесс действовали особые (неслучайные) факторы, которые следует найти и устранить. Необычных структур расположения точек, могущих указывать на наличие других особых факторов, на R-карте не наблюдается. Исключаем выборку номер 3 из дальнейшего рассмотрения. Рассчитываем новые значения CL, UCL, LCL.

;

;

;

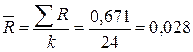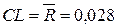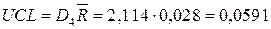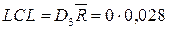(LCL отсутствует).

Вновь полученная R-карта указывает на статистическую управляемость процесса (рисунок 20).

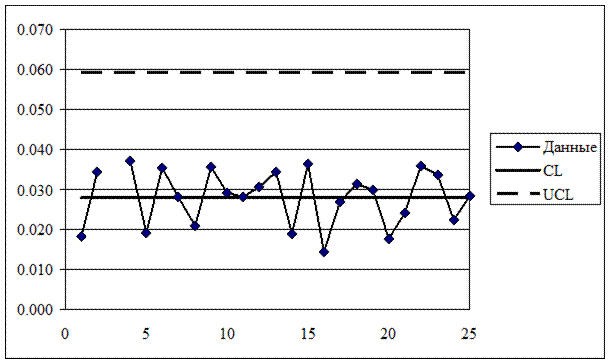
Рисунок 20 – R-карта (исключена выборка номер 3)

Вычисляем CL, UCL, LCL для -карты и строим -карту (рисунок 21). При вычислениях и построении точку 3 из первоначальной выборки исключаем.

;

;

.

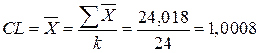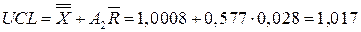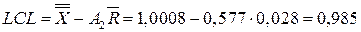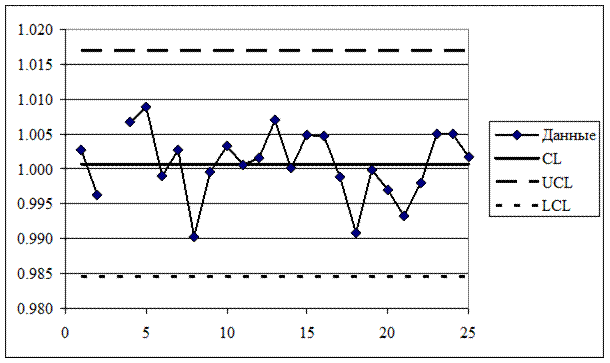
Рисунок 21 – -карта (исключена выборка номер 3)

На вновь полученной R-карте и на -карте все точки лежат внутри контрольных границ. Необычных структур расположения точек не наблюдается. Таким образом, карты, приведенные на рисунках 20 и 21, демонстрируют статистическую управляемость технологического процесса.

Оценим возможность данного процесса производить резисторы с заданными параметрами. Для этого вычислим индекс возможностей технологического процесса PCI.

Определим верхнее UTL и нижнее LTL допустимое значение контролируемого параметра:

UTL=1,05;

LTL=0,95.

Оценку среднеквадратического отклонения определим с помощью коэффициента 1/d₂, взятого из таблицы 2 для n=5:

.

.

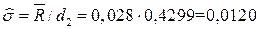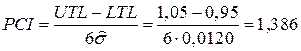Поскольку PCI больше 1,33, считаем, что процесс способен выпускать резисторы требуемого номинала с требуемой точностью. В тоже время, так как процесс находится в статистически управляемом состоянии и PCI лишь незначительно превышает величину 1,33, существенно улучшить процесс, и, например, перейти к выпуску резисторов с погрешностью 2,5% вероятно не удастся без модернизации технологического оборудования.

Определим величины коэффициентов точности и настроенности:

;

.

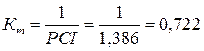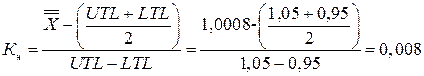Ввиду того, что коэффициенты слишком малы, установить по номограмме (рисунок 18) значение вероятной доли дефектных резисторов не представляется возможным. Однако, можно уверенно утверждать, что она меньше установленной в задании величины 1%. Кроме того, смещение центра настройки 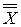от номинального значения контролируемого параметра составляет 0,1%. Дополнительная настройка процесса не требуется.

ЛЕКЦИЯ 13. Статистическое регулирование технологических процессов (часть 2)