Краткие сведения о картах контроля по качественному и альтернативному признакам
Часть сведений о картах контроля по качественному и альтернативному признакам была упомянута в предыдущей лекции.
Напомним их.
Контроль качества продукции, в ходе которого каждую проверенную её единицу относят к определенной группе, а последующее решение о контролируемой совокупности принимают в зависимости от соотношения количеств её единиц, оказавшихся в разных группах, называется контролем по качественному признаку.
Контроль по альтернативному признаку является частным случаем контроля по качественному, когда совокупность продукции состоит из двух групп: годной и дефектной (соответствующей и несоответствующей) продукции. Решение о контролируемой совокупности принимается в зависимости от числа обнаруженных дефектных единиц или числа дефектов, приходящихся на определенное число единиц продукции.
В соответствии с этим контрольные карты Шухарта также разделяют на два типа: карты контроля по количественному признаку и карты контроля по качественному либо альтернативному признаку.
Примерами контрольных карт по альтернативному признаку являются:
- карта долей несоответствующих единиц продукции (p) или карта числа несоответствующих единиц (np);
- карта числа несоответствий (c) или карта числа несоответствий, приходящихся на единицу продукции (u).
Карта для доли несоответствующих (дефектных) изделий (p-карта). В p-карте подсчитывается доля дефектных изделий в выборке. Она применяется, когда объем выборки – переменный.
Карта для числа несоответствующих (дефектных) изделий (np-карта). В np-карте подсчитывается число дефектных изделий в выборке. Она применяется, когда объем выборки – постоянный.
Карта для числа дефектов в выборке (с-карта). В с-карте подсчитывается число дефектов в выборке.
Карта для числа дефектов на одно изделие (u-карта). В u-карте подсчитывается число дефектов на одно изделие в выборке.
1.2 Карта долей несоответствующих единиц продукции (p-карта)
В таблице 9 приведены формулы для построения p-карт.
Таблица 9 – Формулы контрольных границ p-карт
| Статистика | Центральная линия (CL) | 3σ-е контрольные границы (LCL, UCL) | |
| LCL | UCL | ||
| p | 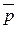
| 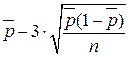
| 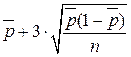
|
Если LCL<0, то граница на карту не наносится и в анализе не участвует.
Как видно из таблицы 9, положение контрольных границ зависит от объема выборок (подгрупп). Если число контролируемых единиц в каждой подгруппе различно, должны быть рассчитаны контрольные границы отдельно для каждого объема выборки. Однако, если объем выборок меняется несущественно, можно ограничиться одним набором контрольных границ, основанным на среднем объеме подгруппы. Для практических целей достаточно, если объемы выборок находятся в пределах ±25% целевого объема выборок. В этом случае в качестве n принимается средний объем выборок.
Используют контрольную p-карту аналогично  -R-карте. Считается, что процесс находится в состоянии статистической управляемости, если все точки p-карты расположены внутри контрольных границ без выбросов, указывающих на наличие особых причин. Точки, выходящие за контрольные границы, исключают, определяют новые контрольные границы, повторно строят карту. Процесс повторяется до тех пор, пока последняя из построенных p-карт не укажет на статистическую управляемость.
-R-карте. Считается, что процесс находится в состоянии статистической управляемости, если все точки p-карты расположены внутри контрольных границ без выбросов, указывающих на наличие особых причин. Точки, выходящие за контрольные границы, исключают, определяют новые контрольные границы, повторно строят карту. Процесс повторяется до тех пор, пока последняя из построенных p-карт не укажет на статистическую управляемость.
1.3 Пример построения и использования p-карты
В таблице 10 указаны количество несоответствующих единиц и общее количество единиц в 25 подгруппах (k=25), полученных при сплошном контроле выключателей с помощью устройства автоматического контроля. Выключатели производят на автоматической сборочной линии. Необходимо с помощью p-карты привести технологический процесс в статистически управляемое состояние.
Таблица 10 – Исходные данные p-карты
| Номер подгруппы (i) | Количество несоответствующих единиц в подгруппе (yi) | Общее количество единиц в подгруппе (ni) | Доля несоответствующих единиц в подгруппе (pi) |
| 0,00128 | |||
| 0,00335 | |||
| 0,00352 | |||
| 0,00160 | |||
| 0,00329 | |||
| 0,00133 | |||
| 0,00322 | |||
| 0,00229 | |||
| 0,00124 | |||
| 0,00000 | |||
| 0,00460 | |||
| 0,00063 | |||
| 0,00425 | |||
| 0,00425 | |||
| 0,00343 | |||
| 0,00476 | |||
| 0,00093 | |||
| 0,00100 | |||
| 0,00185 | |||
| 0,00000 | |||
| 0,00125 | |||
| 0,00288 | |||
| 0,00213 | |||
| 0,00345 | |||
| 0,00260 |
Разброс объемов подгрупп не превышает ±5%. Таким образом, можно использовать общие контрольные границы для всех подгрупп. Вычислим центральную линию 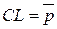 , контрольные границы UCL, LCL.
, контрольные границы UCL, LCL.
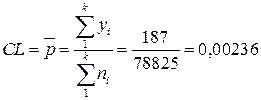 ;
;
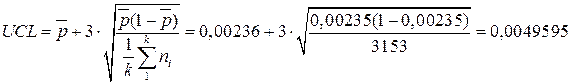 ;
;
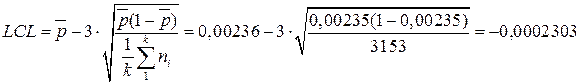 ;
;
Так, как LCL<0, LCL на p-карту не наносим.
p-карта приведена на рисунке 22.
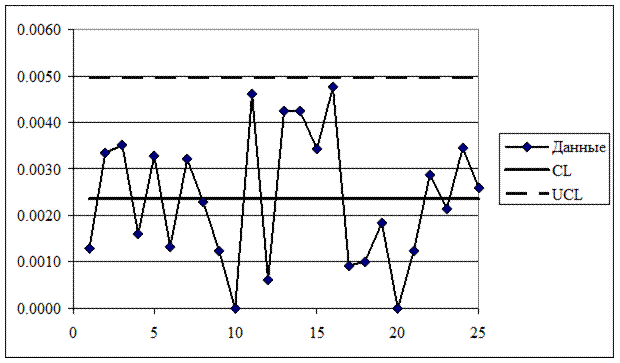
Рисунок 22 – р-карта
Как видно из рисунка 22, все точки p-карты находятся внутри контрольных границ, следовательно, исследуемый технологический процесс находится в статистически управляемом состоянии.
ЛЕКЦИЯ 14. Статистический приемочный контроль
____________________________________________________________________
Изучаемые вопросы:
1. Статистический приемочный контроль.
2. Принципы статистического приемочного контроля.
3. Планы контроля.
4. Автоматизированные системы контроля и управления качеством электронных средств.
Дата добавления: 2020-07-18; просмотров: 565;











