Замененные компоненты.
Дата: 23.09.06
Инженер: Иванов А.А.
Отмечайте так |, ||,
,
|,
Отметки соответствуют числам 1, 2, 3, 4, 5 Наименование Компонента Отметки о количестве Количество Микросхемы
Резисторы
|
Конденсаторы
Всего Рисунок 7 – Пример контрольного листка
ГИСТОГРАММА
Гистограмма –это столбчатый график, построенный по данным, полученным за определенный интервал времени. Данные разбиваются на несколько интервалов, соответствующих столбикам. Высота каждого столбика определяется количеством элементов, попавших в данный интервал. Гистограмма позволяет получить представление о законе распределения случайной величины.
Общий порядок построения гистограмм следующий:
1. Собираются данные контролируемого параметра (xi) за определенный период (месяц, квартал, год и т.д.). Число данных должно быть не менее 30-50, оптимальное число порядка 100.
2. Определяются наибольшее Xmax и наименьшее Хmin значения из всех полученных данных и вычисляется размах R: R = Xmax – Хmin. Размах характеризует разброс контролируемой величины, он определяет ширину гистограммы.
3. Полученный диапазон (размах) делится на несколько интервалов. Число интервалов k зависит от общего числа собранных данных n и некоторых других факторов.
Рекомендуется использовать формулу Стерджеса:
k = 1 + 3,322 lg n . (54)
Также можно использовать формулу:
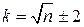 . (55)
. (55)
4. Далее определяют ширину интервала (величина интервала, интервальная разность):
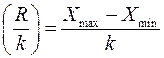 . (56)
. (56)
Все полученные данные распределяют по интервалам. Если какое-то значение попадает на границу, его следует относить к левому по отношению к ней интервалу. Подсчитывается число значений, попавших в каждый интервал mj, где j-номер интервала.
5. Для каждого интервала подсчитывается относительная частота попадания в него данных
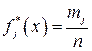 . (57)
. (57)
6. По полученным данным строится гистограмма – столбчатая диаграмма, высота столбиков которой соответствует частоте или относительной частоте попадания данных в каждый из интервалов.
Пример данных для построения гистограммы: Пусть на фрезерном станке изготавливаются пластины, номинальной толщиной 9 мм. Поле допуска на толщину от 6,55 мм до 11,5 мм. Необходимо по значениям толщин группы деталей сделать вывод о состоянии этого станка.
Данные по разбросу деталей приведены в таблице 1
Таблица 1 – Разброс деталей по толщине
| Интервал, мм | 6,55-7,05 | 7,05-7,55 | 7,55-8,05 | 8,05-8,55 | 8,55-9,05 | 9,05-9,55 | 9,55-10,05 | 10,05-10,55 | 10,55-11,05 | 11,05-11,55 | 11,55-12,05 | 12,05-12,55 |
| Количество деталей, попавших в данный интервал, шт. |
Гистограмма, построенная по этим данным, приведена на рисунке 8.
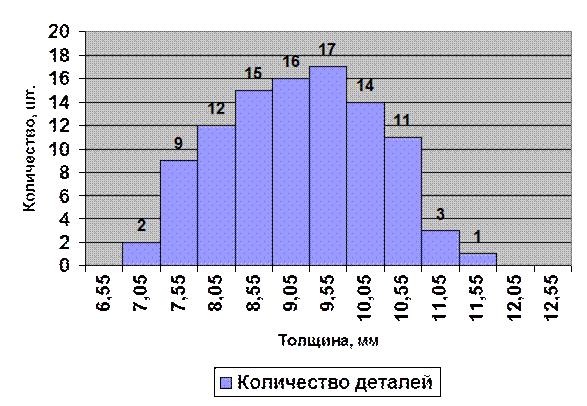
Рисунок 8 – Гистограмма, построенная по данным из примера
Из гистограммы видно, что, несмотря на то, что номинальная толщина 9 мм, больше всего деталей имеют толщину от 9,55 до 10,05 мм. Кроме того, количество деталей с завышенной толщиной больше, чем с заниженной. Это говорит о том, что станок настроен плохо (в сторону больших значений). Фактический разброс не совпадает с полем допуска, т.е. имеет место брак. Ввиду того, что ширина поля допуска и фактический разброс практически одинаковы даже после настройки станка можно ожидать появление брака. Возможно, потребуется заменить станок на более точный, обеспечивающий меньший разброс.
Кроме гистограммы используется полигон (линия, соединяющая середины отрезков на гистограмме) и кумулятивная кривая (КК) (линия, соединяющая правые углы на гистограмме; каждая точка кумулятивной кривой равна сумме всех предыдущих значений).
Примеры кривых распределения, встречающиеся на практике:
а) Поле допуска значительно больше, чем ширина кривой распределения. Брак отсутствует. Используется слишком точный и дорогой станок.
б) Ширина кривой распределения равна ширине поля допуска. Это состояние неустойчиво, стоит чуть сбиться настройкам станка и будет брак.
в) Ширина кривой распределения значительно больше ширины поля допуска. Часть продукции бракованная. Возможно несколько выходов из данной ситуации: приобрести другое оборудование или расширить поле допуска, выбрасывать бракованные детали, сместить центр настройки станка в сторону исправимого брака.
г) Возможно смещение центра настройки станка. Требуется настройка.
д) Если кривая распределения имеет несколько максимумов, то имеет место объединение двух и более распределений, т.е. при построении этой кривой использовались данные двух и более групп деталей, произведенных в разных условиях.
е) Если на кривой нет ярко выраженного максимума, а имеется много значений, близких к максимуму (кривая имеет форму стола). Такая кривая получается в двух случаях: объединены несколько распределений с близкими средними значениями, либо в процессе получения выборки центр настройки оборудования смещался.
ж) Асимметричная кривая распределения имеет место, когда соответствующий технологический параметр имеет односторонне ограничение.
ЛЕКЦИЯ 10. Инструменты контроля качества (часть 2)
____________________________________________________________________
Изучаемые вопросы:
1. Диаграмма разброса.
2. Стратификация.
ДИАГРАММА РАЗБРОСА
Диаграмма разброса – один из инструментов контроля качества, позволяющий визуально определить вид и тесноту связи между двумя случайными величинами. Другое название диаграммы разброса – поле корреляции. В качестве случайных величин наиболее часто выступают:
1 Показатель качества и фактор производства;
2 Два показателя качества;
3 Два фактора производства.
Для построения диаграммы разброса данные собирают парами. На диаграмме разброса одной паре данных соответствует одна точка разброса. Считается, что точек должно быть не менее 25-30.
Рассмотрим случай, когда в качестве одной из случайных величин выступает показатель качества, другой – фактор производства.
Последовательность применения диаграммы разброса для этого случая будет состоять из следующих этапов:
1 Осознание неудовлетворенности качеством изделия в целом, его деталей и узлов или качеством технологического процесса.
2 Выбор показателя качества, количественно отражающего эту неудовлетворенность.
3 Выдвижение гипотезы о влиянии какого-либо фактора производства на выбранный показатель качества.
4 Сбор парных данных, т.е. значений показателей качества и факторов производства.
5 Построение диаграммы разброса и её анализ. В результате анализа диаграммы может быть сделан один из следующих выводов:
5.1 Связь присутствует и достаточно сильна: выбранный фактор производства сильно связан с показателем качества, выдвинутая гипотеза верна. В этом случае, изменяя фактор производства, можно добиться требуемого значения показателя производства и, тем самым, улучшить качество. Требуемое изменение фактора производства количественно можно оценить с использованием уравнения прямой выборочной регрессии.
5.2 Связь присутствует, но не достаточно сильная: выбранный фактор производства слабо связан с показателем качества. Изменяя данный фактор, можно до некоторой степени управлять показателем качества, однако необходимо продолжить поиск факторов, так же влияющих на этот показатель, выдвинув новые гипотезы. Следует, не исключая из рассмотрения текущего фактора производства, найти другие факторы, влияющие на показатель качества, выполнив п.3 - п.5 описываемой последовательности. Требуемое качество может быть достигнуто одновременным изменением всех выявленных влияющих факторов производства.
5.3 Связь не установлена: выбранный фактор производства не связан с показателем качества, гипотеза неверна. Продолжаем поиск факторов. Следует найти факторы производства, влияющие на показатель качества, исключив при поиске из рассмотрения текущий фактор. Новый поиск также проводится в соответствии с последовательностью п.3 - п.5.
Дополнительная информация:
· Следует отметить, что если две переменные кажутся связанными, это не означает, что они таковыми являются.
· Если данные не кажутся связанными, это не означает, что они не связаны: просто приведено недостаточно данных или данные следует разбить по классам и построить по каждому классу свою диаграмму, а возможно допущена большая ошибка при измерении и т. д.
Построение диаграммы разброса необходимо проводить в следующей последовательности:
1 Собрать парами значения (x1,y1), (x2,y2), ... (xn,yn) случайных величин X и Y, между которыми требуется исследовать зависимость. Расположить их в таблицу. Желательно не менее 25-30 пар данных.
2 Найти максимальные и минимальные значения для X и Y. Выбрать шкалы на горизонтальной и вертикальной осях так, чтобы их длины были приблизительно одинаковыми. Если одна переменная – фактор производства, а вторая – показатель качества, то выбрать для фактора горизонтальную ось, а для показателя качества – вертикальную.
3 Нанести точки, соответствующие парам данным, на диаграмму.
4 Сделать все необходимые обозначения. Убедиться, что нижеперечисленные данные, отраженные на диаграмме, понятны любому человеку, а не только тому, кто делал диаграмму:
4.1 Название диаграммы.
4.2 Интервал времени, когда были получены данные.
4.3 Число пар данных.
4.4 Названия и единицы измерения для каждой оси.
4.5 Условия получения данных.
4.6 Имя человека, сделавшего диаграмму.
Типичные варианты скопления точек на диаграмме разброса приведены на рисунке 9.
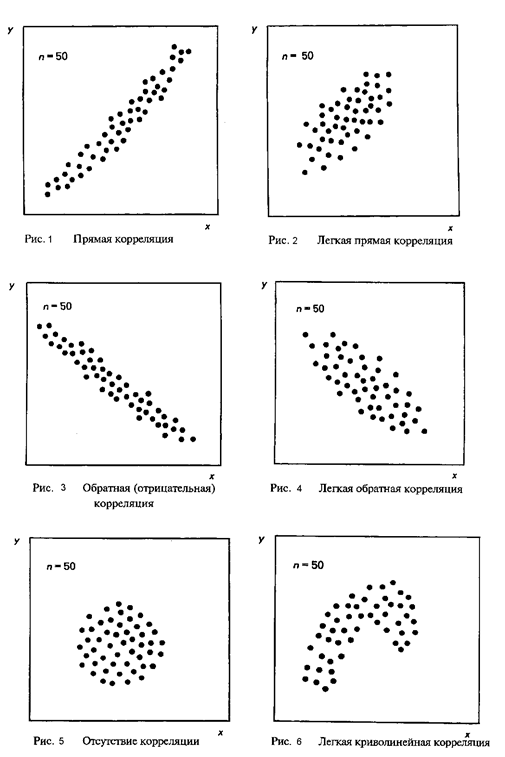
Рисунок 9 – Типичные варианты скопления точек на диаграмме разброса
На графике (рис.1) рисунка 9 изображена сильная прямая корреляция. Величины X и Y связаны. Увеличивая X можно увеличить Y.
На графике (рис.2) рисунка 9 изображена легкая (слабая) прямая корреляция. Величины X и Y связаны, однако на величину Y кроме Х действую какие-либо другие величины. Увеличивая X также можно увеличить Y.
На графике (рис.3) рисунка 9 изображена сильная обратная корреляция. Величины X и Y связаны. Увеличивая X можно уменьшить Y.
На графике (рис.4) рисунка 9 изображена легкая (слабая) обратная корреляция. Величины X и Y связаны, однако на величину Y кроме Х действую какие-либо другие величины. Увеличивая X также можно уменьшить Y.
На графике (рис.5) рисунка 9 приведено скопление точек, характерное для отсутствия корреляции. Величины X и Y не связаны.
На графике (рис.6) рисунка 9 изображена криволинейная корреляция. Величины X и Y связаны, в отличие от случаев (рис.1) – (рис.4) нелинейной зависимостью.
Если при анализе диаграммы разброса установлена связь между случайными величинами X и Y, то, изменяя X, можно добиться требуемого значения Y (или наоборот). Если при этом выявленная связь может считаться линейной, то количественное изменение одной из случайных величин, необходимое для получения определенного значения другой, может быть найдено с помощью уравнения прямой выборочной регрессии.
Пусть в результате n испытаний получены пары значений случайных величин X и Y:
(x1,y1), (x2,y2),.....(xn,yn). (58)
Допустим, что случайная величина Y имеет вид
Y=Y0+V, (59)
где Y0 – случайная величина, связанная с Х линейной функциональной зависимостью (формула 60),
V – случайная величина, отражающая влияние на Y неизвестных случайных факторов.
Y0=kX+b, (60)
где k и b – некоторые неизвестные постоянные.
Если бы V=0, то все точки поля корреляции, соответствующие парным данным, принадлежали бы прямой
y=kx+b. (61)
Данное уравнение является уравнением прямой выборочной регрессии.
Таким образом, одна из задач корреляционного анализа заключается в отыскании по опытным данным коэффициентов линейной зависимости (60).
Пусть величина
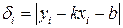 (62)
(62)
выражает степень удаленности точки i от прямой (61). Чем меньше разности 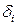 в совокупности, тем «ближе» проходит прямая (61) от множества точек (58), тем лучше она отражает искомую зависимость. Пусть «расстояние» от прямой до системы точек выражается равенством:
в совокупности, тем «ближе» проходит прямая (61) от множества точек (58), тем лучше она отражает искомую зависимость. Пусть «расстояние» от прямой до системы точек выражается равенством:
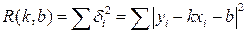 . (63)
. (63)
Наилучшей прямой, т.е. прямой с меньшим «расстоянием» от совокупности точек (58), будет являться такая прямая, которая соответствует минимуму функции R(k,b).
Минимум функции R(k,b) достигается в точке с координатами:
 , (64)
, (64)
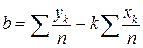 . (65)
. (65)
Прямая (61), для которой сумма квадратов (63) достигает наименьшего значения, называется прямой выборочной регрессии. Если чертой сверху обозначить среднее значение соответствующей величины, то выражения (64, 65) можно записать в виде:
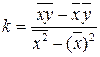 , (66)
, (66)
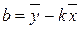 . (67)
. (67)
Число  , равное значению функции R(k,b), где k и b определены из равенств (64, 65) называется остаточной дисперсией.
, равное значению функции R(k,b), где k и b определены из равенств (64, 65) называется остаточной дисперсией.
Для определения тесноты связи случайных величин используют коэффициент корреляции
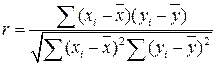 . (68)
. (68)
Коэффициент корреляции обладает следующими свойствами:
1) r=0 если величины X и Y не связаны.
2) |r|=1 если величины X и Y связаны зависимостью вида (61).
Необходимо заметить, что коэффициент корреляции (68) корректно отражает тесноту связи случайных величин, если зависимость между ними линейная.
СТРАТИФИКАЦИЯ
Стратификацияпо-другому называетсярасслаиванием.
В соответствии с этим методом данные о причинах появления брака разделяют на группы в зависимости от условий их получения и производят обработку каждой группы в отдельности. Группы называют слоями (стратами), а сам процесс разделения – расслаиванием (стратификацией).
В производственных процессах используют метод 5М, разделяя данные в зависимости от человека (man), материала (material), машины (machine), метода (method), измерения (measurement).
Расслаивание осуществляется следующим образом:
1 по работникам (исполнителям) (квалификация, опыт, стаж работы и т.д.);
2 по материалам, сырью, комплектующим (вид, марка, партия, производитель и т.д.);
3 по технологическому оборудованию и оснастке (фирма, вид оборудования, срок эксплуатации и т.д.);
4 по методу производства (технические приемы, температура, давление, другие параметры технологических процессов и т.д.);
5 по способу получения измерительной информации (используемые методы измерения, вид оборудования, класс точности и т.д.)
Если при расслаивании присутствует разница между слоями, это является исходной информацией о причинах появления брака.
В результате расслаивания должны выполняться два условия:
1 разница между значениями данных одного условия (дисперсия) должна быть меньше, чем в совокупности;
2 разница между средними значениями слоев должна быть как можно больше.
Расслаивание может осуществляться многократно.
Пример расслаивания: При анализе причин задержек поставок каких-либо деталей типичными факторами для расслоения могут быть:
- срок оформления заказа (строгое соблюдение даты оформления заказа),
- наличие оформления заказа,
- вид и сложность деталей.
Например, есть предприятие, на котором мы работаем – Предприятие №1. Предприятие №2 – другое предприятие, у которого Предприятие №1 заказывает детали. У Предприятия №3 Предприятие №1 заказывает части деталей.
Таким образом, получаем: заказ Предприятием №1 у Предприятия №2 – первичный заказ, а заказ Предприятием №2 у Предприятия №3 – вторичный заказ.
Данные для расслаивания приведены в таблице 2. В данном случае для удобства в одной таблице приведены данные для двух вариантов развития событий (соответственно, Таблица 2 (числитель) и Таблица 2 (знаменатель)) с одинаковым итоговым общим количеством случаев, а также с одинаковыми общими значениями количества случаев по оформлению заказа в соответствии с установленной датой, по оформлению заказа с опозданием, по выполнению заказа в срок, по выполнению заказа с опозданием.
Первое предположение: расслаивание по соблюдению даты оформления заказа.
Таблица 2 – Данные для расслаивания (два варианта)
| Оформление заказа | Выполнение заказа, число случаев | Всего случаев | |
| В срок | С опозданием | ||
| В соответствии с установленной датой | 21 6 | 2 17 | |
| С опозданием | 3 18 | 42 27 | |
| Всего случаев |
По данным таблицы 2 (числитель) видно, что строгое соблюдение даты оформления заказа ведет к значительному улучшению ситуации со сроками поставок (уменьшение задержек). Если ситуация складывается как в таблице 2 (числитель), то мы нашли причину задержек поставок: оформление заказа с опозданием.
Если ситуация складывается как в таблице 2 (знаменатель), то этого утверждать нельзя. В этом случае необходимо произвести дополнительное расслаивание, например по виду деталей (таблица 3)
Таблица 3 – Расслаивание таблицы 2 (знаменатель) по виду деталей
| Детали | Выполнение заказа, число случаев | Всего случаев | |
| В срок | С опозданием | ||
| А | |||
| В | |||
| С | |||
| D | |||
| E | |||
| F | |||
| Всего случаев |
Из таблицы 3 видно, что основное количество задержек поставок относится к деталям А, В, С. Очевидно, следует найти причину этого.
Пусть в результате дальнейшего анализа было видно, что эти детали требуют дополнительной обработки, которая выполняется Предприятием №3 по вторичному заказу от Предприятия №2. Кроме того было выяснено, что детали D, F, не требующие дополнительной обработки из-за перегруженности Предприятия №2 также иногда передаются по вторичному заказу.
Прояснить ситуацию поможет расслаивание по факту наличия или отсутствия вторичного заказа (таблица 4).
Таблица 4 – Расслаивание таблицы 2 (знаменатель) по факту наличия или отсутствия вторичного заказа
| Вторичный заказ | Выполнение заказа, число случаев | Всего случаев | |
| В срок | С опозданием | ||
| Имеет место | |||
| Отсутствует | |||
| Всего случаев |
В результате проведенных расслаиваний было окончательно установлено, что задержки поставок возникают из-за присутствия вторичного заказа. В этой ситуации можно наметить следующие меры по решению проблемы:
1) информацию о больших заказах доводить до предприятия-поставщика (Предприятия №2) заблаговременно;
2) скорректировать объемы заказов таким образом, чтобы выполнение их было по силам предприятию-поставщику и не вынуждало Предприятие №2 выполнять вторичные необоснованные заказы на Предприятии №3
3) помочь Предприятию №2 наладить эффективные взаимоотношения с Предприятием №3
ЛЕКЦИЯ 11. Инструменты контроля качества (часть 3)
____________________________________________________________________
Изучаемые вопросы:
1. Диаграмма Исикавы.
2. Диаграмма Парето.
3. Кружки контроля качества.
ДИАГРАММА ИСИКАВЫ
Диаграмма Исикавы(причинно-следственная диаграмма) также часто называется «рыбья кость» или «рыбий скелет». Она позволяет выявить, систематизировать и наглядно представить причины, оказывающие влияние на рассматриваемую проблему. Качество изделия, выражающееся в показателях качества, является результатом взаимодействия множества причин, факторов производства, и для того, чтобы выпускать только качественные изделия, необходимо к наиболее важным показателям качества, которые в данном случае рассматриваются как следствие, поставить в соответствие факторы и условия производства, являющиеся причинами.
Диаграмма Исикавы (причинно-следственная диаграмма, «рыбья кость», «рыбий скелет») демонстрирует отношения между проблемой и ее возможными причинами. Обеспечивает модель установления связей между проблемой и факторами, влияющими на нее. Диаграмма Исикавы полезна для устранения причин появления проблем, а также полезна для понимания эффектов воздействия нескольких факторов на процесс. Анализируются четыре основных причинных фактора: человек, машина (оборудование), материал и метод работ. При анализе этих факторов выявляются вторичные, третичные и т.д. причины, приводящие к дефектам и подлежащие устранению. Для анализа дефектов и построения диаграммы необходимо определить максимальное число причин, которые могут иметь отношение к допущенным дефектам. Такую диаграмму еще называют диаграммой «4М» по составу основных факторов.
Для составления причинно-следственной диаграммы необходимо подобрать максимальное число факторов, имеющих отношение к характеристике, которая вышла за пределы допустимых значений. При этом для исследования причин явления необходимо привлекать и третьих лиц, не имеющих непосредственного отношения к работе, так как у них может оказаться неожиданный подход к выявлению и анализу причин, которого могут не заметить лица, привычные к данной рабочей обстановке.
Наиболее эффективным считается групповой метод анализа причин, называемый «мозговым штурмом».
Порядок построения причинно-следственной диаграммы условий и результатов следующий:
1. Определение цели. Например, провести систематизацию причин и условий, влияющих на снижение качества изделий. Или систематизировать условия, влияющие на расходы по устранению брака, или проанализировать условия, влияющие на спрос продукции на рынке. Желательно, чтобы анализируемая проблема имела количественное измерение. Например, качество технологической операции может оцениваться долей брака, количеством дефектов определенного вида величиной отклонения от заданных значений, наконец, численной величиной какого-либо параметра изделия или детали. Расходы могут измеряться в денежном выражении, затратах времени, материалов, комплектующих и т. п.
2. Составление списка факторов и условий, которые влияют или могут влиять на рассматриваемую проблему. При этом полезным будет метод «мозгового штурма», позволяющий в короткое время собрать идеи и мнения различных людей по данной проблеме. При составлении списка факторов нельзя отбрасывать ни одного из них. Маловероятные и незначительные факторы могут быть отброшены и не рассматриваться при последующем анализе, но на схеме они должны быть представлены, чтобы было ясно, что они уже рассматривались на каком-то этапе анализа.
3. Группировка факторов по их естественному родству в группы и подгруппы с различной степенью детализации. При анализе проблем, связанных с качеством продукции, обычно, рассматриваются следующие группы: технология, оборудование, методы измерения, персонал, материалы, организация производства, внешние условия.
4. Построение схемы. Схема позволяет наглядно показать множество факторов, систематизированных в определенном порядке, что существенно облегчает поиски правильных решений. Пример схемы приведен на рисунке 10.
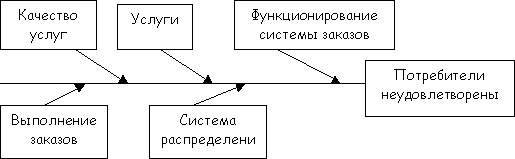
Рисунок 10 – Пример построения схемы при построении диаграммы Исикавы (причинно-следственной диаграммы)
Пример окончательного вида диаграммы Исикавы для анализа качества некоторого технологического процесса приведен на рисунке 11.
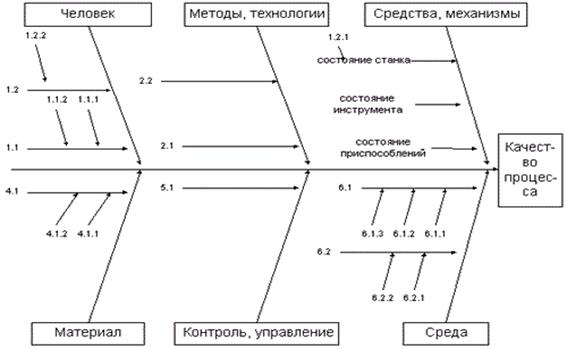
Рисунок 11 – Пример окончательного вида диаграммы Исикавы для анализа качества некоторого технологического процесса
ДИАГРАММА ПАРЕТО
Диаграмма Парето – это инструмент, позволяющий распределить усилия для разрешения возникающих проблем и выявить основные причины, с которых нужно начинать действовать. В большинстве случаев подавляющее число дефектов и связанных с ними потерь возникают из-за относительно небольшого числа причин. Метод анализа Парето заключается в классификации проблем качества на немногочисленные, но существенно важные и многочисленные, но несущественные. Он позволяет распределить усилия и установить основные факторы, с которых нужно начинать действовать с целью преодоления возникающих проблем.
Различают два вида диаграмм Парето:
1. Диаграмма Парето по результатам деятельности. Предназначена для выявления главной проблемы и отражает нежелательные результаты деятельности, связанные:
· скачеством (дефекты, поломки, ошибки, отказы, рекламации, ремонты, возвраты продукции);
· ссебестоимостью (объем потерь; затраты);
· со срокамипоставок (нехватка запасов, ошибки в составлении счетов, срыв сроков поставок);
· с безопасностью (несчастные случаи, трагические ошибки, аварии).
2. Диаграмма Парето по причинам. Отражает причины проблем, возникающих в ходе производства, и используется для выявления главной из них:
· исполнитель работы: смена, бригада, возраст, опыт работы, квалификация, индивидуальные характеристики;
· оборудование: станки, агрегаты, инструменты, оснастка, организация использования, модели, штампы;
· сырье: изготовитель, вид сырья, завод-поставщик, партия;
· метод работы: условия производства, заказы-наряды, приемы работы, последовательность операций;
· измерения: точность (указаний, чтения, приборная), верность и повторяемость (умение дать одинаковое указание в последующих измерениях одного и того же значения), стабильность (повторяемость в течение длительного периода), совместная точность, тип измерительного прибора (аналоговый или цифровой).
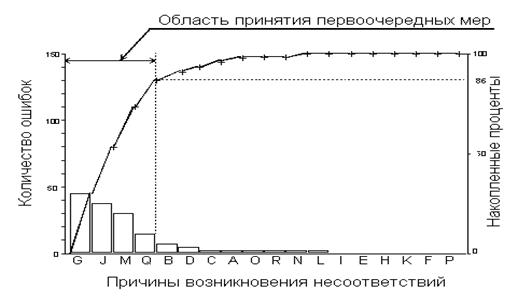
Рисунок 12 – Пример диаграммы Парето по причинам
Построение диаграммы Парето начинают с классификации возникающих проблем по отдельным факторам (например, проблемы, относящиеся к браку; проблемы, относящиеся к работе оборудования или исполнителей, и т.д.). Затем следуют сбор и анализ статистического материала по каждому фактору, чтобы выяснить, какие из этих факторов являются превалирующими при решении проблем.
В прямоугольной системе координат по оси абсцисс откладывают равные отрезки, соответствующие рассматриваемым факторам, а по оси ординат – величину их вклада в решаемую проблему. При этом порядок расположения факторов таков, что влияние каждого последующего фактора, расположенного по оси абсцисс, уменьшается по сравнению с предыдущим фактором (или группой факторов). В результате получается диаграмма, столбики которой соответствуют отдельным факторам, являющимся причинами возникновения проблемы, и высота столбиков уменьшается слева направо. Затем на основе этой диаграммы строят кумулятивную кривую.
Дата добавления: 2020-07-18; просмотров: 551;











