ПЕРВООБРАЗНАЯ И ИНТЕГРАЛ. ИЗ ИСТОРИИ.

Понятие интеграла и интегральное исчисление возникли из потребности вычислять площади любых фигур и поверхности и объемы произвольных тел. Предыстория интегрального исчисления восходит к глубокой древности. Идея интегрального исчисления была древними учеными предвосхищена гораздо в большей мере, чем идея дифференциального исчисления.

В продолжении ряда занятий мы познакомимся с основными понятиями, научимся использовать их. А сейчас просто короткая историческая справка:

АРХИМЕД (287-212 г.г. до н.э.)– его вклад в подготовку фундамента для создания интегрального исчисления огромен.

Для дальнейшего развития зачаточных интеграционных методов Архимеда необходимо было предварительно создать и развить новую алгебру с ее символикой, ввести понятия переменных, функции, и т.д.

Первые значительные попытки развития интеграционных методов Архимеда, увенчавшиеся успехом, были предприняты в XVII в., когда, с одной стороны, были достигнуты значительные успехи в области алгебры, а с другой – все более интенсивно развивались экономика, естествознание, техника, требовавшие более общих и мощных математических методов изучения и вычисления величин.

1609 г. – ИОГАНН КЕППЛЕР (1571-1630 г.г.)– опубликованы два закона движения планет, во втором из которых уже были предприняты попытки применения методов Архимеда.

1615 г. – ИОГАНН КЕППЛЕР – «Новая стереометрия винных бочек» - о вычислении площадей плоских фигур и поверхностей и объемов тел.

В то же время этими вопросами занимался Бонавентура Кавальери (ок. 1598-1647 г.г.), которого интересовали не практические задачи, а общая постановка и трактовка проблемы. Его труды сыграли большую роль в создании исчисления, но в них было много пробелов и недостатков.

Последователями Кавальери были ДЖОН ВАЛЛИС (1616-1703 г.г.) – «Арифметика бесконечных» (1655 г.), ПЬЕР ФЕРМА (1601-1665 г.г.) – вычисление интегралов для степени 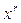(1644 г.), БЛЕЗ ПАСКАЛЬ (1623-1662 г.г.) –«Трактат о синусе четверти круга» (1658 г.)

Признавая огромные заслуги Б.Паскаля, следует, однако, отметить, что он не пользовался новой символической алгеброй и не производил алгебраических выкладок, он все выражал словами, что лишило его возможности создать новый общий алгоритм, который открыли И.Ньютон и Г.Лейбниц.

1686 г. – ГОТФРИД ВИЛЬГЕЛЬМ фон ЛЕЙБНИЦ (1646-1716 г.г.) –«О глубокой геометрии и анализе неделимых, а также бесконечных» - первая печатная работа по интегральному исчислению, в которой установлена связь между интегральным и дифференциальным исчислениями.

Независимо от Г.Лейбница и еще до него эти результаты были получены ИСААКОМ НЬЮТОНОМ (1643-1727 г.г.),который нашел их, идя совсем по другому пути.

1671 г. – ИСААК НЬЮТОН– «Метод флюксий»(флюксия - производная) – хотя к основным понятиям и алгоритму исчисления И.Ньютон пришел в середине 60-х г.г. XVII в., когда двадцатилетний Г.Лейбниц был студентом юридического факультета и математикой не занимался.

В XVIII в. наибольший вклад в развитие и популяризацию дифференциального и интегрального исчислений внес ЛЕОНАРД ЭЙЛЕР (1707-1783 г.г.), написавший 3-хтомник по математическому анализу (1748, 1755, 1768-1769 г.г.). На трудах Л.Эйлера воспитывалось целое поколение математиков второй половины XVIII в. и первой четверти XIX в.

Далее развитием интегрального и дифференциального исчислений занимались ЖОЗЕФ ЛУИ ЛАГРАНЖ (1736-1813 г.г.), ОГЮСТЕН КОШИ (1789-1857 г.г.), БЕРНХАРД РИМАН (1826-1866 г.г.).Большой вклад внесли русские математикиМИХАИЛ ВАСИЛЬЕВИЧ ОСТРОГРАДСКИЙ (1801-1862 г.г.) И ПАФНУТИЙ ЛЬВОВИЧ ЧЕБЫШЕВ (1821-1894 г.г.).Работы П.Чебышева в области анализа и его приложений были успешно продолжены его ученикамиА.М. ЛЯПУНОВЫМ (1857-1918 г.г.), В.А.СТЕКЛОВЫМ(1864-1923 г.г.), С.Н.БЕРНШТЕЙНОМ (1880-1968 г.г.).

Глубокие исследования, предпринятые в области анализа в конце XIX в. и начале XX в., связаны с развитием теории функций, теории множеств и других отраслей современной математики.

I. ПЕРВООБРАЗНАЯ ФУНКЦИЯ. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ.

Основной задачей дифференциального исчисления является нахождение производной или дифференциала данной функции.