Броуновское движение

Важнейшим фактором, влияющим на молекулярно-кинетические свойства золей, является броуновское движение частиц дисперсной фазы. Оно названо в честь английского ботаника Роберта Броуна, который впервые наблюдал его в 1827 г., исследуя под световым микроскопом взвесь цветочной пыльцы в воде. Ученый обнаружил, что частицы пыльцы непрерывно двигаются по сложным траекториям ни на мгновение не оставаясь в покое. Причину данного движения долгое время установить не могли и считали его проявлением особенностей исключительно живой материи. Однако такое объяснение вскоре было отвергнуто, т.к. обнаружили, что подобное непрерывное движение могут совершать и неорганические частицы, взвешенные в жидкости или газе.

Таким образом, была установлена универсальность броуновского движения.

Дальнейшие исследования показали, что отдельные частицы двигаются совершенно независимо одна от другой. Их перемещение происходит тем интенсивнее, чем меньше размеры частиц и вязкость среды и совершенно не зависят от природы измельченного вещества.

В свободно-дисперсных системах с газовой или жидкой дисперсионной средой коллоидные частицы также не зафиксированы в каких-то определенных позициях. Они участвуют в броуновском движении, которое является прямым следствием теплового движения молекул растворителя и их беспорядочных ударов о данную частицу. Причем чем меньше размеры частицы, тем меньшее число молекул ударяется о ее поверхность. Это, в свою очередь, приводит к тому, что различия по числу и силе ударов с каждой стороны частицы становятся более значительными. Частица в любой момент времени движется в ту сторону, с которой результирующая величина ударов меньше. Само ее движение является скачкообразным и хаотическим. Скачки совершаются с большой частотой и в произвольном направлении, то есть независимо от того каким был предшествующий скачок. Кроме того, скачки имеют разную длину. Установлено, что коллоидная частица изменяет направление своего движения приблизительно 10¹² раз за 1 секунду. Проследить действительный путь частицы при

Мариан Смолуховский, (1872 – 1917), польский физик-теоретик. Окончил университет в Вене (1894), в 1896-1897 работал в университетах Парижа, Глазго и Берлина. С 1900 профессор Львовского университета (позднее ректор), с 1913 профессор Краковского университета. Основные труды по статистической физике. Работы Смолуховского по теории флуктуаций (1904) и броуновского движения (1906) наряду с работами Альберта Эйнштейна являются основополагающими в этой области. Смолуховский создал на основе теории броуновского движения кинетическую теорию коагуляции коллоидов, теорию электрокинетических явлений, заложив фундамент кинетической теории коллоидных систем.

таком движении не представляется возможным. Поэтому за меру, характеризующую интенсивность броуновского движения, принимают так называемое смещение частицы или ее сдвиг (∆Х). Это проекция расстояния между двумя положениями частицы (А и В) за время t, разделяющее два смежных наблюдения (рис. 56).

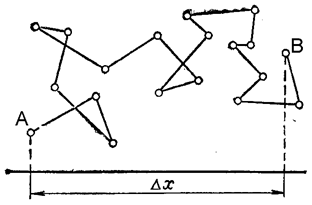
Рис. 56. Схема броуновского движения частицы

Смещения частицы за одинаковые промежутки времени t обычно не совпадают как по величине, так и по направлению, поэтому на практике используют так называемый среднеквадратичный сдвиг частицы :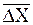

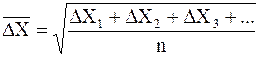
где ∆Х₁, ∆Х₂, ∆Х₃, … – отдельные проекции смещения частицы за одно и тоже время t;

n – число определяемых проекций смещения частицы за определенное время t.

Точную количественную оценку броуновского движения частицы можно дать с помощью уравнения Смолуховского-Эйнштейна:

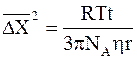
где N_А – число Авогадро;

η – вязкость дисперсионной среды;

r – радиус частицы дисперсной фазы;

T – температура раствора;

t – время, за которое происходит смещение частицы.

Таким образом, скорость броуновского движения коллоидных частиц изменяется лишь в зависимости от их радиуса и вязкости дисперсионной среды. При этом природа самой частицы на ее движение влияния не оказывает.

Если размеры и масса частиц дисперсной фазы превышают определенные пределы, вероятность взаимной компенсации ударов с различных направлений оказывается значительно выше.

Так частицы размером 4 · 10^{-6 м ÷ 5 · 10-6 м совершают только небольшие колебательные движения около некоторого центра. При более крупных размерах частиц их броуновское движение в любом виде не наблюдается.}

В связи с этим грубодисперсные системы не обладают молекулярно-кинетическими свойствами. Именно на этом отличии базируется классификация дисперсных систем на высокодисперсные и грубодисперсные.

Основной причиной движения крупных дисперсных частиц служит различие плотностей дисперсной фазы (ρ_ф) и дисперсионной среды (ρ_с). Если плотность дисперсной фазы больше (ρ_ф > ρ_с), то частицы постепенно оседают вниз под действием силы тяжести. Этот процесс называют седиментацией. Более легкие дисперсные частицы (ρ_с > ρ_ф), наоборот, постепенно всплывают вверх. Этот процесс называют обратной седиментацией.

Диффузия

Под влиянием теплового и броуновского движения происходит самопроизвольный процесс выравнивания концентраций частиц по всему объему коллоидного раствора. Этот процесс называется иначе диффузией. Диффузия частиц в золях подчиняется тем же законам, что и диффузия молекул либо ионов в истинных растворах и газах, но протекает в сотни раз медленнее из-за гораздо больших размеров частиц.

Количественно процесс диффузии характеризуется коэффициентом диффузии D, который показывает какое количество вещества проходит через поперечное сечение раствора площадью 1 м² в течение секунды при градиенте (разности) концентраций по разные стороны сечения равном единице. А. Эйнштейн, изучая броуновское движение, установил связь коэффициента диффузии D со средним сдвигом частицы:

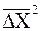= 2Dt

С учетом определения значения 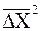из верхнего уравнения можно выделить D:

D =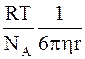

Данные уравнения имеют очень большое значение в коллоидной химии, т.к. позволяют на основании измерений коэффициента диффузии D определить радиус взвешенных коллоидных частиц сферической формы.