Пример расчета напряженности Электрического поля равномерно заряженного тонкого кольца

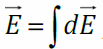
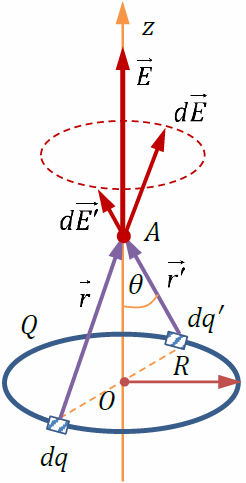По тонкому кольцу равномерно распределён заряд Q > 0. Находим напряжённость электрического поля в точке A на оси кольца (OA = z). Разобьём кольцо на точечные заряды dq(на рисунке показаны два малых заряда dqи dq′, равные по модулю и расположенные диаметрально противоположно). По принципу суперпозиции полей – где dE - напряжённость электрического поля малого заряда dq.

Векторы напряжённости электрического поля каждого из этих зарядов одинаковы по модулю и направлены так, что концы этих векторов образуют конус с вершиной в точке A (штриховой линией показано основание этого конуса). Проекции этих векторов на плоскость кольца компенсируются, поэтому суммарный вектор направлен вдоль оси z: E (при z > 0). Вычислим Ez. Напряжённость поля точечного заряда:

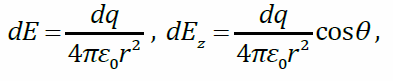
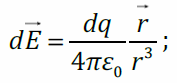Величины r иθ (угол) одинаковы для всех элементов dq:

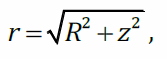
подставим

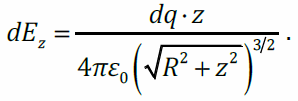
В этом выражении все величины – постоянные, кроме dq. Проинтегрируем по q:

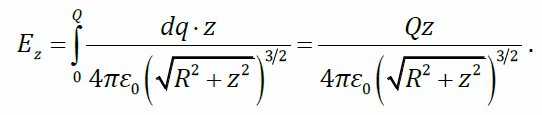
Поток вектора напряженности. Теорема Остроградского-Гауса для электростатического поля в вакууме. Применение теоремы к расчету напряженности поля. Пример: поле бесконечно большой равномерно заряженной плоскости.

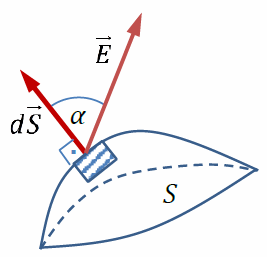Введем новую физическую величину, характеризующую электрическое поле – поток вектора напряженности электрического поля(Φ).

Элементарный поток направлен по внешней нормали к малому участку dS (Если поверхность S не замкнута, то выбор одного из двух направлений нормали произволен, при этом направление нормали для всех участков dSдолжно быть одинаковым)

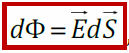
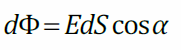
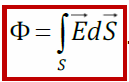
Полный поток вектора сквозь поверхность S E

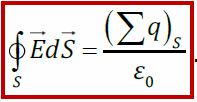
Теорема Остроградского-Гаусса для :поток вектора напряжённости электрического поля сквозь произвольную замкнутую поверхность равен алгебраической сумме зарядов, охваченной этой поверхностью, делённой на ε0:

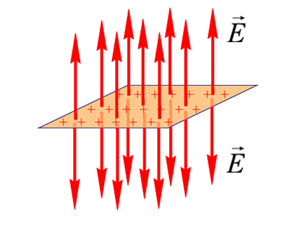
Поле равномерно заряженной бесконечной плоскости:
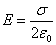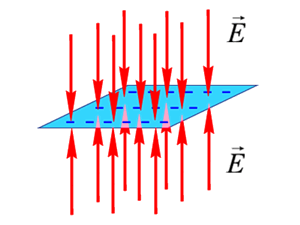
, где 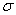— поверхностная плотность заряда.

Работа сил электростатического поля по перемещению заряда. Потенциал электростатического поля. Связь между напряженностью поля и потенциалом. Понятие градиента. Методы расчета потенциала. Пример: потенциал на оси равномерно заряженного кольца.

I уравнение Максвелла для электростатического поля умножим на пробный заряд q0:

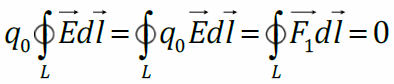
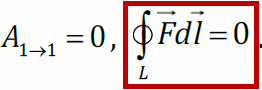Работа электростатического поля по перемещению пробного заряда по произвольной замкнутой траектории равна нулю. Это означает, что электростатическое поле потенциально. Потенциальная энергиязаряженной частицы в электростатическом поле равна работе внешних сил при перемещении этой частицы из точки, где потенциальная энергия принята равной нулю, в данную точку, или работе поля при этом перемещении: 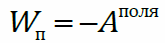.Потенциальная энергия – характеристика и поля, и заряда: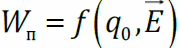

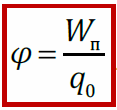Потенциалом электростатического поля [φ] = В (вольт) называется физическая величина, равная отношению потенциальной энергии заряда q₀ в данной точке пространства, к величине этого заряда.

Разность потенциалов – это работа поля по перемещению пробного заряда из начального положения в конечное, отнесённая к модулю этого заряда и взятая с обратным знаком, или работа внешних сил при том же перемещении, отнесённая к модулю пробного заряда.