Интегральная связь напряжённости и потенциала электростатического поля
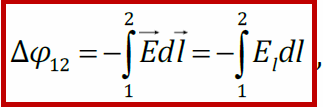
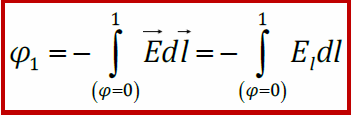 – потенциал поля в точке 1.
– потенциал поля в точке 1.
Элементарная работа поля 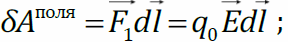 элементарное приращение потенциала
элементарное приращение потенциала 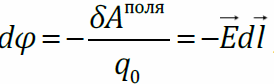
 – дифференциальная связь напряжённости и потенциала электростатического поля.
– дифференциальная связь напряжённости и потенциала электростатического поля.
Градие́нт -вектор, своим направлением указывающий направление наибольшего возрастания некоторой величины  , значение которой меняется от одной точки пространства к другой, а по величине (модулю) равный быстроте роста этой величины в этом направлении.
, значение которой меняется от одной точки пространства к другой, а по величине (модулю) равный быстроте роста этой величины в этом направлении.
Потенциал – непрерывная функция координат! График потенциала никогда не имеет разрывов.
Методы расчёта потенциала электростатического поля: метод суперпозиий и интегральная связь Еи φ.
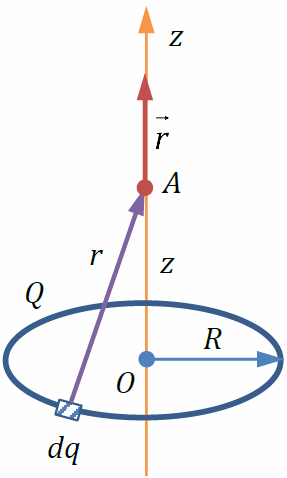 Пример: Поле равномерно заряженного тонкого кольца
Пример: Поле равномерно заряженного тонкого кольца
По тонкому кольцу равномерно распределён заряд Q > 0 . Пусть потенциал равен нулю в бесконечно удалённой точке. Разобьём кольцо на малые участки с зарядами dqи воспользуемся методом суперпозиций: 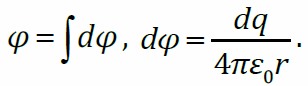 Расстояние r до точки A, где измеряется потенциал, одинаково для всех элементов dq:
Расстояние r до точки A, где измеряется потенциал, одинаково для всех элементов dq:  . Проинтегрируем выражение для потенциала по q:
. Проинтегрируем выражение для потенциала по q:  Найдём напряжённость электрического поля как функцию z через дифференциальную связь напряжённости и потенциала:
Найдём напряжённость электрического поля как функцию z через дифференциальную связь напряжённости и потенциала: 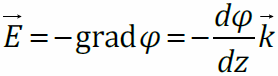 .
. 
Этот же результат можно получить методом суперпозиции (билет №2)
Потенциал электростатического поля. Связь между напряженностью поля и потенциалом (интегральная и дифференциальная). Примеры расчета потенциала электростатического поля. Диполь в электростатическом поле.
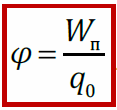
Потенциалом электростатического поля [φ] = В (вольт) называется физическая величина, равная отношению потенциальной энергии заряда q0 в данной точке пространства, к величине этого заряда.
 Разность потенциалов – это работа поля по перемещению пробного заряда из начального положения в конечное, отнесённая к модулю этого заряда и взятая с обратным знаком, или работа внешних сил при том же перемещении, отнесённая к модулю пробного заряда.
Разность потенциалов – это работа поля по перемещению пробного заряда из начального положения в конечное, отнесённая к модулю этого заряда и взятая с обратным знаком, или работа внешних сил при том же перемещении, отнесённая к модулю пробного заряда.
Дата добавления: 2016-07-05; просмотров: 10278;











