В дальнейших расчетах следет пользоваться только фактическими
передаточными числами!
Обозначим фактическое передаточное число редуктора Uф = uф1 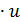 ф2, где uф1 и
ф2, где uф1 и 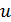 ф2 – соответственно передаточного числа первой и второй ступеней.
ф2 – соответственно передаточного числа первой и второй ступеней.
Отклонение фактического передаточного числа редуктора от заданного значения u определяется по формуле:
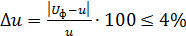 . (24)
. (24)
Если отклонение 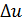 больше
больше 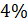 , необходимо соответственно изменить передаточное число второй ступени, не изменяя её стандартного межосевого расстояния.
, необходимо соответственно изменить передаточное число второй ступени, не изменяя её стандартного межосевого расстояния.
Определим межосевые делительные расстояния:
для первой ступени 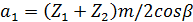 ; (25)
; (25)
для второй ступени 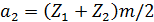 .
.
Числовое значение межосевого расстояния для первой ступени а1 должно совпасть со стандартным значением. Это можно отрегулировать, изменяя в допустимых пределах значение угла наклона зуба β.
Если межосевое расстояние для второй ступени 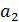 будет отличаться от стандартного, то его необходимо изменить путем применения зубчатых колес со смещением исходного контура, то есть за счёт корригирования зубчатых колёс.
будет отличаться от стандартного, то его необходимо изменить путем применения зубчатых колес со смещением исходного контура, то есть за счёт корригирования зубчатых колёс.
Расчет коэффициента суммы смещения 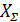 при заданном межосевом расстоянии
при заданном межосевом расстоянии 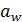 производится следующим образом. Определяется коэффициент воспринимаемого смещения (для прямозубой передачи:
производится следующим образом. Определяется коэффициент воспринимаемого смещения (для прямозубой передачи: 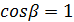 ):
):
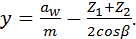 (26)
(26)
Определим вспомогательные величины А и Б ( 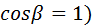 :
:
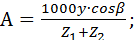 (27)
(27)
Б – определим по номограмме по значению А (рис. 3)
Коэффициент уравнительного смещения (для прямозубой передачи 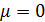 ):
):
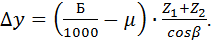 (28)
(28)
Коэффициент суммы смещений:
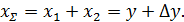 (29)
(29)

Рис. 3. Номограмма для определения вспомогательной величины Б
при заданном межосевом расстоянии aw (α=200, aw >a)
Если 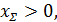 принимаем
принимаем 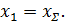 Это следует понимать так: положительное смещение исходного контура обеспечивается за счёт увеличения диаметра заготовки колеса под нарезку зуба, профиль зуба формируется более удалённым от основной окружности участком эвольвенты. В результате повышается контактная и изгибная прочность зуба. Поэтому положительное смещение целесообразно применить для самого слабого зубчатого колеса – шестерни с наименьшим числом зубьев.
Это следует понимать так: положительное смещение исходного контура обеспечивается за счёт увеличения диаметра заготовки колеса под нарезку зуба, профиль зуба формируется более удалённым от основной окружности участком эвольвенты. В результате повышается контактная и изгибная прочность зуба. Поэтому положительное смещение целесообразно применить для самого слабого зубчатого колеса – шестерни с наименьшим числом зубьев.
Если 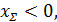 следует принять
следует принять 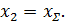 В этом случае небольшое ослабление ведомого зубчатого колеса практически не снизит долговечность зубчатой передачи. Это колесо воспринимает за ресурс такое число циклов нагружений, которое в несколько раз меньше, чем воспринимает шестерня.
В этом случае небольшое ослабление ведомого зубчатого колеса практически не снизит долговечность зубчатой передачи. Это колесо воспринимает за ресурс такое число циклов нагружений, которое в несколько раз меньше, чем воспринимает шестерня.
Результаты расчетов параметров зубчатых колес представлены в табл. 11.
Таблица 11. Основные параметры зубчатых колес редуктора
| Параметр | Расчетная формула | Косозубая передача | Прямозубая передача | |||||||
| Ш1 | К1 | Ш2 | К2 | |||||||
| Межосевое расстояние, мм | aw | |||||||||
| Нормальный модуль, мм | m | 3,5 | ||||||||
| Делительный диаметр, мм | d=mZ / cosβ | 34,74 | 245,26 | 80,5 | ||||||
| Начальный диаметр, мм | dw1 = 2aw/(uф+1) dw2 = 2awuф/(uф+1) | 34,74 | 245,26 | 80,39 | 279,61 | |||||
| Диаметр вершин зубьев, мм | da =d+2(1+x-Δу)m | 38,74 | 249,26 | 87,5 | 286,5 | |||||
| Диаметр впадин зубьев, мм | df =d – (2,5 – 2x)m | 29,74 | 240,26 | 71,75 | 270,76 | |||||
| Ширина венца колеса, мм предварительная окончательная | b2′ - табл. 10 b2 – табл. 13 | |||||||||
| Суммарное число зубьев | ZΣ | |||||||||
| Действительная величина наклона зуба | β =arccos[ZΣm/2aw] | 11°53′ | 0° | |||||||
| Число зубьев | Z1 =ZΣ/(1 + uф) Z2 = ZΣ - Z1 | |||||||||
| Передаточное число | uф = Z2/ Z1 | 7,059 | 3,478 | |||||||
| Коэффициент смещения исходного контура | x (ф-ла 29) | 0,07 | ||||||||
| Коэффициент уравнительного смещения | Δу | |||||||||
| Нормальный исходный контур | – | по ГОСТ 13755-81 | ||||||||
| Степень точности по ГОСТ 1643-81 | Принимаем | 8-В | 8-В | |||||||
Для предотвращения подрезания ножки зуба, если 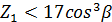 , также необходима коррекция. При
, также необходима коррекция. При 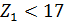 и
и 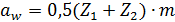 рекомендуется принимать высотную коррекцию:
рекомендуется принимать высотную коррекцию: 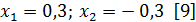 . Если за счет смещения исходного контура не удается достигнуть стандартного межосевого расстояния, следует изменить число зубьев колеса. После коррекции межосевое расстояние
. Если за счет смещения исходного контура не удается достигнуть стандартного межосевого расстояния, следует изменить число зубьев колеса. После коррекции межосевое расстояние 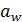 проверяют на соответствие стандартному значению по формуле:
проверяют на соответствие стандартному значению по формуле:
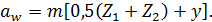 (30)
(30)
Дата добавления: 2016-07-05; просмотров: 2791;











