Направление химических реакций.

Энергия Гиббса

Если процесс протекает так, что DН = 0 (изолированная система), то изменение энтропии становится его единственной движущей силой.

При условии DS = 0 единственной движущей силой химической реакции является убыль энтальпии.

Таким образом, в химических реакциях одновременно проявляются две тенденции:

1) стремление системы к образованию связей в результате взаимного притяжения частиц, что приводит к увеличению порядка и сопровождается понижением энергии системы;

2) стремление к диссоциации сложных частиц на простые, увеличению числа частиц, увеличению беспорядка и возрастанию энтропии.

Первая тенденция в изобарно-изотермических условиях характеризуется энтальпийным факторомпроцесса и количественно выражается через DН.Вторая - характеризуется энтропийным фактором и количественно выражается произведением абсолютной температуры на энтропию, т.е. TDS.

Если эти тенденции уравновешивают друг друга, то DН = TDS.

При неравенстве этих величин их разность может служить мерой химического сродствареагентов. Она называется энергией Гиббса и вычисляется по уравнению:

DG = DH - TDS

При постоянстве температуры и давления химические реакции могут самопроизвольно протекать только в таком направлении, при котором энергия Гиббса системы уменьшается (DG< 0)(вторая формулировка II закона термодинамики).

Из уравнения (4.6) вытекает, что наибольшее сродство веществ друг к другу проявляется в реакциях, протекающих с DН < 0 и DS > 0 .

Чем меньше величина DG⁰_х.р, тем дальше система находится от состояния химического равновесия и тем более она реакционноспособная.

Изменение энергии Гиббса (DG_х.р.) в результате химической реакции можно найти по стандартным энергиям Гиббса образования веществ (DG⁰_ƒ) (табл. 4.1):

DG⁰_х.р. = å n_прод·DG⁰_{ƒ, прод} - å n_{реагентов}·DG⁰_{ƒ, реагентов .}

При этом DG⁰_ƒ простых веществ так же, как DН⁰_ƒ и DU⁰_ƒ, равны нулю.

Таким образом, критерий направления процессов можно записать так:

равновесие - DG = 0; DН = Т·DS;

(реакция может протекать как в прямом, так и в обратном направлении);

самопроизвольный процесс

в прямом направлении DG < 0; DН - Т·DS < 0;

не может протекать в прямом направлении

(возможен обратный процесс) DG > 0; DН - Т·DS > 0.

Переход DG через ноль можно определить из соотношения

DН = Т_равн·DS . Отсюда .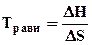

Таким образом, энергия Гиббса зависит от характера реакции (значения DН и DS) и от температуры. Зная величины DН и DS, можно рассчитать DG и, соответственно, предсказать возможность или невозможность самопроизвольного протекания реакции, а также влияние температуры на направление процесса.

Пример 8. Пользуясь данными табл. 4.1, установить возможность или невозможность восстановления диоксида титана в стандартных условиях по реакции:

TiO_{2 (к)} + 2С_{(графит)} = Ti _(к) + 2СО_(г) .

Решение. В таблице 5.1 находим значения DG⁰_ƒ (в кДж/моль) для TiO₂ (-888,6) и СО (-137,1) и рассчитываем DG⁰:

DG⁰ = 2DG⁰_ƒ (СО) - DG⁰_ƒ (TiO₂) = 2·-137,1 - (-888,6) = 614,4 кДж.

Поскольку DG⁰ > 0, восстановление TiO₂ при 298 К невозможно. Согласно закону сохранения энергии для обратного процесса окисления титана оксидом углерода DG⁰ = - 614,4 кДж, т.е. обратный процесс возможен.

Пример 9. Реакция восстановления Fe₂O₃ водородом протекает по уравнению:

Fe₂O_{3 (к)} + 3H₂ = 2Fe _(к) + 3Н₂О_(г), DH⁰ = + 96,61кДж.

Возможна ли эта реакция при стандартных условиях, если изменение энтропии DS⁰ = 0,1387 кДж/моль ·К? При какой температуре начнется восстановление Fe₂O₃?

Решение. Вычисляем DG⁰ реакции по:

DG⁰= DH⁰ -TDS⁰ = 96,61 - 298×0,1387 = 55,28 кДж.

Так как DG >0, то реакция при стандартных условиях невозможна; наоборот, при этих условиях идет обратная реакция окисления железа (коррозия). Найдем температуру согласно уравнению (4.8), при которой DG = 0 (состояние равновесия):

DH⁰ = T·DS⁰ , отсюда .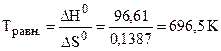

Следовательно, при температуре примерно 696,5 К начнется реакция восстановления Fe₂O₃. (“Примерно” потому, что при решении задачи мы не учитываем слабую зависимость DН и DS от температуры). Иногда эту температуру называют температурой начала реакции.

Пример 10. При некоторой температуре Т эндотермическая реакция А ® Впрактически идет до конца. Определить знак DS реакции.

Решение. То, что реакция протекает самопроизвольно в прямом направлении, указывает на то, что DG < 0. Так как реакция эндотермическая, то DH > 0. Из уравнения

DG = DH - T·DSследует, что ·DS⁰должна быть > 0.

Пример 11.Не проводя расчётов, определить, какие из перечисленных процессов возможны в изолированной системе:

а) 2NH_{3 (г)} = N_{2 (г)} + 3H_{2 (г) ,}

б) NО _(г) + NО_{2 (г)} = N₂О_{3 (к)} ,

в) 2S_(к) + 3O_{2 (г)} = 2SO_{3 (г)} .

Решение.В изолированной системе (DH = 0) критерием самопроизвольного протекания процесса является увеличение энтропии. Учитывая, что газообразные вещества имеют большую энтропию, чем жидкие и твердые, заключаем, что с увеличением энтропии протекает реакция (а) (из 2 моль газа получается 4 моль). Реакции б) и в) протекают в обратном направлении (в реакции б) из газообразных веществ получилось кристаллическое, а реакция (в) сопровождается уменьшением объема газа).

Пример 12.Указать, какие из реакций образования оксидов азота и при каких температурах (высоких или низких) могут протекать самопроизвольно в стандартных условиях:

а) 2N_{2 (г)} + О₂ = 2N₂О _(г) , DH⁰₂₉₈ > 0.

б) 2N_{2 (г)} + О₂ = 2NО _(г) , DH⁰₂₉₈ > 0.

в) NО _(г) + NО_{2 (г)} = N₂О_{3 (к)} , DH₂₉₈^O < 0.

Решение.а) определим изменение энтропии: так как количество газа уменьшается с трех молей до двух, энтропия уменьшается и DS < 0. Возможность протекания реакции определяется энергией Гиббса (DG < 0). Из анализа уравнения (4.6) DG = DH - TDS следует, что при DH^O > 0 и DS < 0 DG > 0 при любых температурах, т.е эта реакция невозможна при любых температурах;

б) аналогично реакции (а);

в) для этой реакции энтропия уменьшается, так как из газообразных веществ получается кристаллическое, т.е. DS < 0. Если DH^O < 0 и DS < 0, то реакция возможна при достаточно низких температурах, при этом величина DH^O будет превышать по абсолютному значению член TDS и DG < 0.