Способ параллакса. Симметричность предмета и его изображения в плоском зеркале

В предшествующей лабораторной работе 4 так же, как и в некоторых Дальнейших работах, приходится отыскивать место, где находится изображение. Для такой дели весьма удобно применять способ параллакса.

Для этого берут длинную (вязальную) спицу и, либо укрепив ее в небольшой подставке (например пробке, деревянной розетке), либо просто, держа спицу в руке, помещают спицу там, где должно находиться изображение — в данном случае за стеклом. Смотря сквозь стекло по нормали к его плоскости, спицу ставят так, чтобы она казалась совпадающей с изображением булавки, стоящей перед стеклом. Можно смотреть на верхний край стекла, тогда спица должна служить продолжением изображения булавки в стекле.

В обоих случаях изображения булавки и спицы окажутся установленными на одной прямой — на луче зрения, но это еще не означает, что они совпадают совершенно: они могут лежать на разных расстояниях от глаза. Чтобы этот вопрос решить, прибегают к способу параллакса, именно: смещают глаз К (рис. 240) в какую-нибудь сторону (например налево) в положение L; тогда, если изображение D и спица F не совпадают, они сместятся относительно друг друга; из рисунка 240 видно, что более далекий предмет смещается в ту е сторону, куда сместился глаз, а более близкий — в противоположную сторону. Это правило и этот прием позволяют, таким образом, выяснить различие в расстоянии двух предметов от наблюдателя.

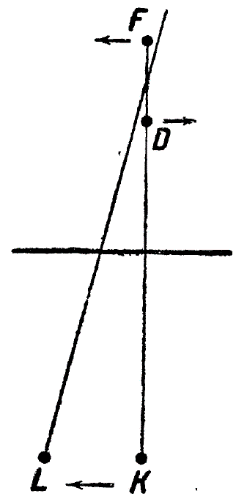
Рис. 240. Способ параллакса

Вывод такой: надо для спицы найти такое место, при котором не будет происходить параллактического смещения ее относительно искомого изображения.

Опыт Сильвануса Томсона. 1) Стекло. 2) Два штатива. 3) Две свечи. 4) Гвоздь (L = 8—10 см) или палочка на небольшой подставке. 5) Спички.

Установив стекло и две свечи так же, как в опыте 3, перед стеклом ставят вертикально гвоздь или вообще стержень (палочку, карандаш) (рис. 241). При зажигании передней свечи получаем от гвоздя две тени: А — от непосредственно падающих лучей и В — от отраженных стеклом лучей. Убирая стекло и зажигая заднюю свечу, увидим, что она даст такую же тень В, какую давали отраженные лучи, т. е. какую давало изображение передней свечи в стекле.

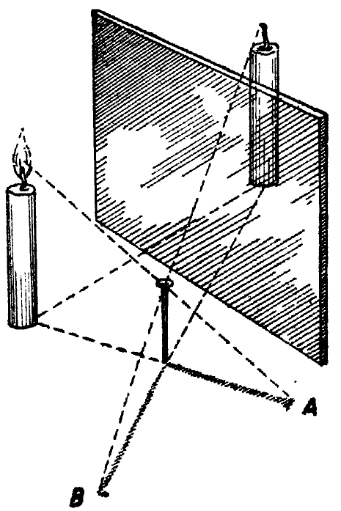
Рис. 241. Опыт Сильвануса Томсона

Симметричность предмета и его изображения в плоском зеркале. 1) Большое плоское зеркало (около 30 см х 40 см). 2) Фигура, начерченная на белом картоне.

Вопрос о том, какое изображение получается в плоском зеркале, разрешается учащимися с большим трудом. Часто они высказывают мнение, что изображение как-то повертывается, и мысль о симметричности совсем не приходит им в голову; поэтому эту симметричность надо показать на нескольких примерах.

1) На белом картоне чертится тушью (толщина линий около 3 мм) разносторонний треугольник АВС (рис. 242, 1, справа). В зеркале виден треугольник, симметричный с данным (рис. 242, 1, слева).

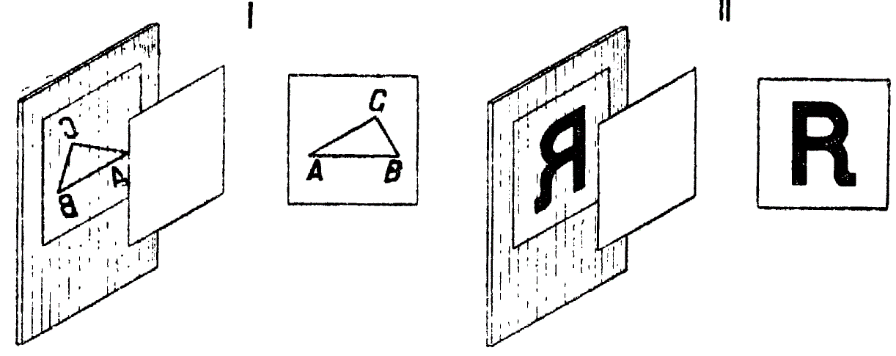
Рис. 242. Изображения в плоском зеркале

2) В зеркале показывают изображение правой руки — видна левая. 3) Французская буква „эр“ (R) в зеркале принимает форму буквы „я“ (Я) (рис. 242, 2).

Множественность изображений в зеркале. 1) Зеркало из толстого стекла 2) Кусок толстого зеркального стекла.

Каждое стекло и зеркало имеют две отражающие поверхности и потому дают вообще несколько изображений подобно параллельным зеркалам. Однако, чтобы заметить и показать эту множественность изображений, надо, во-первых, применять толстые стекла (h = 1,5—2 см).

Во-вторых, необходимо смотреть не перпендикулярно к зеркалу, а под возможно меньшим углом к его плоскости. Для наблюдения надо взять предмет, оканчивающийся острием (рис. 259).

Рис. 259. Множественность изображений в зеркальном стекле

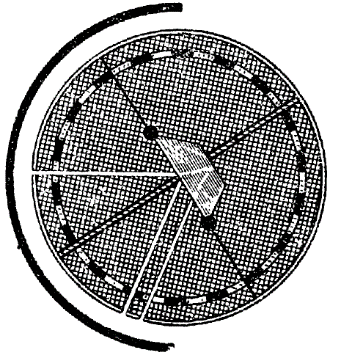
Рис. 260. Шайба Гартля (отражение от наружной и внутренней поверхностей стекла)

При сильном источнике света удается показать два луча, отраженных от передней и задней поверхностей плоско-параллельной пластинки (рис. 260) на шайбе Гартля (рис. 180).