Высота расположения центра тяжести автомобилей, м
| Автомобиль | ВАЗ-2106 | М-2140 | ГАЗ-24 | УАЗ-469 | ГАЗ-53 | ГАЗ-66 | ЗИЛ-130 | МАЗ-5335 |
| Без груза | 0,56 | 0,562 | 0,552 | - | 0,749 | 0,763 | 0,885 | 1,050 |
| Полностью нагруженый | 0,581 | 0,596 | 0,620 | 0,769 | 1,152 | 1,150 | 1,340 | 1,450 |
Реакции опорной поверхности на колеса автомобиля
Нагрузки на опорную поверхность от колес при движении автомобиля не остаются постоянными и зависят от величины ускорения или замедления автомобиля, высоты центра тяжести, силы сопротивления воздуха, угла подъема или спуска дороги и т.д.
Изменение этих нагрузок и равных им реакций со стороны дороги могут быть значительными и оцениваются коэффициентами изменения реакций, представляющими собой отношения реакций при движении автомобиля к реакциям, когда автомобиль неподвижен и располагается на горизонтальной дороге. Коэффициенты изменения реакций (m1 – для передних колес и m2 – для задних колес автомобиля) находятся отдельно.
Величины реакций могут быть найдены путем составления суммы моментов всех действующих на автомобиль сил и моментов относительно какой-либо точки автомобиля (рис. 28). Для определения нормальных реакций N1, действующих на передние колеса со стороны дороги, составляется сумма моментов относительно точки С – центра пятен контаетов задних колес. Чтобы определить нормальные реакции N2, действующие на задние колеса, составляется сумма моментов относительно центра пятна контакта передних колес – точки В. Например, для определения реакции N2:
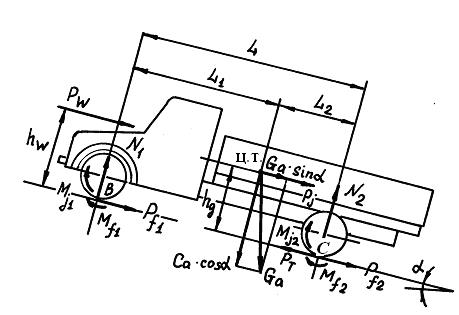
Рис. 28. Силы и моменты, действующие
на автомобиль
N2 × L – M¦1 – M¦2 – Gа× sin a × hg – Pj × hg – Ga cos a ×L1– Pw hw – Mj1– Mj2 = 0,
N2 = (M¦1 + M¦2 + Gа× sin a × hg + Pj × hg + Ga cos a ×L1+ Pw hw + Mj1+ Mj2) / L
где L – база автомобиля; M¦1 и M¦2 – моменты сопротивления качению передних и задних колес автомобиля; Mj1 и Mj2 – инерционные моменты передних и задних колес; Ga ×sin a – проекции вектора силы тяжести автомобиля на плоскость, параллельну опорной поверхности; Ga ×cos a – проекция вектора силы тяжести автомобиля на плоскость, перпендикулярную опорной поверхности; hg – высота расположения центра тяжести автомобиля; hw – высота расположения метацентра автомобиля; Pw – сила сопротивления воздуха движению автомобиля; Pj – сила инерции автомобиля (направлена вперед при замедлении автомобиля или назад – при разгоне).
Испытаниями установлено, что коэффициенты изменения реакций равны:
для передних колес m1 = 0,8...1,4; для задних колес m2 = 1,2...1,4.
С учетом угла продольного уклона дороги – a, коэффициента сцепления колес с дорогой – j, высоты расположения центра тяжести автомобиля – hg, коэффициенты изменения реакций могут быть найдены по следующим зависимостям:
m1 = 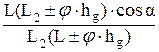 ; (7)
; (7)
m2 = 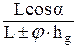 . (8)
. (8)
В этих выражениях знак “+ “ – для случая разгона автомобиля, знак “–“ – для случая торможения.
Реакции, действующие на правые и левые колеса автомобиля, движущегося по дороге с закруглением, имеющей, кроме того, боковой уклон, могут быть определены с помощью суммы моментов всех действующих на автомобиль сил и моментов относительно центров пятен контактов этих колес (рис. 29).
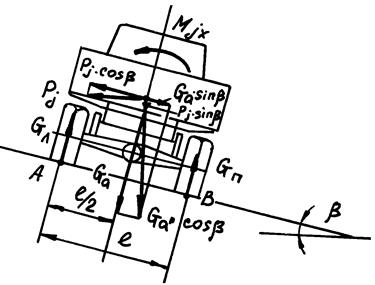 Составим сумму моментов, лействующих на автомобиль относительно центра пятна контакта левых колес – точки А, и определим реакции, действующие на правые колеса – Gпр'. Составив сумму моментов относительно точки В, определим реакции, действующие– на левые колеса – Gл' :
Составим сумму моментов, лействующих на автомобиль относительно центра пятна контакта левых колес – точки А, и определим реакции, действующие на правые колеса – Gпр'. Составив сумму моментов относительно точки В, определим реакции, действующие– на левые колеса – Gл' :
Pj sin b × l/2 + Ga cos b × l /2 +
+ Mjx – Pj cos b ×hg + Gпр' × l +
+ Ga sin b ×hg = 0 ,
где Pj – сила инерции дейст-
вующая на автомобиль в попе-
речном направлении; l – колея Рис. 29. Реакции, действующие на автомобиля.
правые и левые колеса автомобиля Откуда
Pj sin b × l/2 + Ga cos b × l/2 + Mjx – Pj cos b ×hg+ Ga sin b ×hg
Gпр' = ¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾ .
l
Аналогично может быть выражена и реакции, действующие на левые колеса – Gл'.
Считается, что силы Gл' и Gпр' распределяются между передними и задними колесами движущегося на повороте с постоянной скоростью автомобиля так же как и при неподвижном его состоянии.
Боковые реакции, действующие на колеса движущегося на повороте автомобиля, показаны на рис. 30.
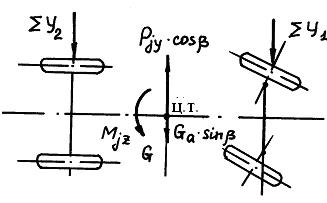
Рис. 30. Боковые реакции, действующие на колеса автомобиля
Составив сумму моментов всех действующих на автомобиль боковых сил последовательно вокруг точек А и В, а также учитывая инерционный момент Mjz вокруг вертикальной оси, проходящей через центр тяжести, находим реакции SУ1 и SУ2.
Mjz + Pjycos b×L2 – Ga sin b ×hg
SУ1 = ¾¾¾¾¾¾¾¾¾¾¾¾¾ ; (9)
L
Mjz + Pjycos b ×L1 + Ga sin b × L1
SУ2 = ¾¾¾¾¾¾¾¾¾¾¾¾¾ . (10)
L
Инерционный момент Mjz равен
Mjz = Jz× 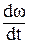 =
= 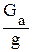 ×r2 ×
×r2 × 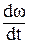 , (11)
, (11)
где Jz – момент инерции; r – радиус инерции автомобиля вокруг вертикальной оси; 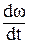 – угловое ускорение, с которым автомобиль поворачивается вокруг вертикальной оси.
– угловое ускорение, с которым автомобиль поворачивается вокруг вертикальной оси.
Таким же образом могут быть найдены инерционные моменты Mjy вокруг продольной и поперечной осей.
Сила инерции Pjx, действующие на автомобиль , двиэущийся прямо, определяются
Pjx = 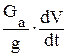 ;
;
Поперечная сила инерции Pjx, действующие на автомобиль, движущийся наповороте с постоянной скоростью
Pjy = 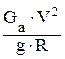 ,
,
где Ga – вес автомобиля (в ньютонах), Н; g – ускорение свободного падения,
м/с2; 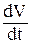 – продольное ускорение или замедление, м/с2; V – скорость автомо-
– продольное ускорение или замедление, м/с2; V – скорость автомо-
билля, м/с; R – радиус поворота до продольной оси автомобиля, м.
Если скорость автомобиля на повороте переменная, например, автомобиль движется с ускорением, продольная сила инерции Рjх может быть определена по выражению
Pjx = 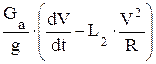 . (12)
. (12)
Первая составляющая в скобках – окружное ускорение автомобиля при его повороте вокруг точки О, являющейся центром поворота автомобиля (рис. 31), вторая составляющая – центростремительное ускорение автомобиля, появляю щееся одновременно с окружным ускорением вследствие поворота автомобиля еще вокруг центра заднего моста – точки К, равное L2w2
Аналогично может быть определена поперечная сила инерции Pjу.. В этом случае первая составляющая в скобках – центростремительное ускорение при повороте вокруг точки О, равное R w2 , второе – окружное ускорение вокруг точки В.
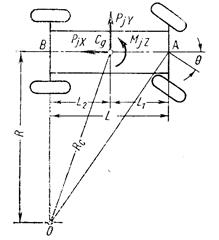 Рjy =
Рjy = 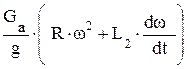 ;
;
Используя приведенных ниже зависимости и рис. 30, получим выражение для определения
поперечной силы инерци  и Pjу:
и Pjу:
R  =
= 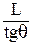 ; w =
; w = 
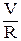 =
= 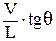 ;
;
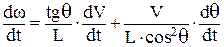 ;
; 
cos θ = 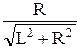 ;
; 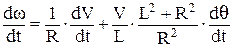 ;
;
Рис. 31.Силы и момеиты,
действующие на автомобиль
Рjy = 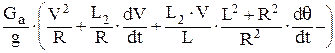 , (13)
, (13)
где 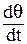 – угловое ускорение автомобиля; L – база автомобиля; L2 – расстояние от центра масс автомобиля до оси задних колес; θ – средний угол поворота управляемых колес; V – скорость автомобиля.
– угловое ускорение автомобиля; L – база автомобиля; L2 – расстояние от центра масс автомобиля до оси задних колес; θ – средний угол поворота управляемых колес; V – скорость автомобиля.
Если движение на закруглении дороги равномерное, сила инерции автомобиля может быть определена
Рj = 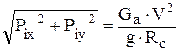 ,
,
где Rc – радиус поворота автомобиля, равный расстоянию от центра поворота автомобиля до его центра тяжести.
Моменты инерции автомобиля вокруг осей координат могут быть определены экспериментально. Расположив центр координат в центре тяжести автомобиля, приняв ось Х проходящей вдоль автомобиля, У – поперек, а Z – вертикально, известными способами находим наиболее важные для эксплуатационных показателей моменты инерции вокруг поперечной и вертикальной осей. Так для определения момента инерции Jy' вокруг поперечной оси передний мост автомобиля устанавливается на пружинную подставку с жесткостью С, на которой он может раскачиваться вокруг оси заднего моста. Обозначив период качания через Т, базу автомобиля через L, момент инерции вокруг оси заднего моста находим по выражению:
Jy' = 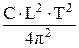 . (14)
. (14)
Далее определяется момент инерции вокруг поперечной оси, проходящий через центр тяжести автомобиля – Jy:
Jy = Jy' – Mп × R2 , (15)
где Мп – подрессоренные массы автомобиля; R – расстояние от центра тяжести до оси заднего моста.
Момент инерции подрессоренной массы автомобиля относительно поперечной оси Jу определяется также методом подвеса, рекомендуемым в отраслевой нормали ОН 025 305 – 67 (рис. 32). При этом замеряются тпериод колебаний и расстояние от центра тяжести подрессоренной массы от оси подвеса.
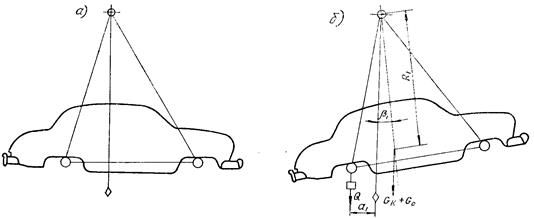
Рис. 32. Определение момента инерции автомобиля методом подвеса
Jу = Jу1 – 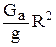 ,
,
где Jу1 - момент инерции относительно поперечной оси подвеса, кг×м2; R – расстояние от центра тяжести подрессоренной массы от оси подвеса, м; Ga – вес автомобиля, Н (кг×м/с2)
Согласно отраслевой нормали ОН 025 307 - 67
Jу1 = 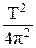 ×GaR,
×GaR,
где Т – период колебаний, с.
Момент инерции вокруг поперечной оси влияет на колебания автомобиля в продольной плоскости и, следовательно, может использоваться для расчета и оценки плавности хода. Короткобазные легковые автомобили с малыми моментами инерции склонны к "галопированию" и отличаются плохой плавностью хода. Поэтому комфортабельные автомобили имеют всегда значительную длину.
Момент инерции вокруг вертикальной оси влияет на управляемость автомобиля. Чем больше этот момент, тем труднее повернуть автомобиль. Для длинных представительских легковых автомобилей, эксплуатирующихся на хороших дорогах, этот фактор не имеет существенного значения. Автомобили же, которые развивают высокую скорость на крутых поворотах, например, спортивные, выполняются с малыми моментами инерции вокруг вертикальной оси. Для этого на таких автомобилях все тяжелые узлы и агрегаты двигатель, топливный бак и др. размещаются ближе к центру масс.
Определение момента инерции вокруг вертикальной оси, проходящей через центр тяжести, может быть выполнено, например, с помощью подвесов, на которых автомобилю задаются колебательные движения вокруг этой оси (рис. 33).
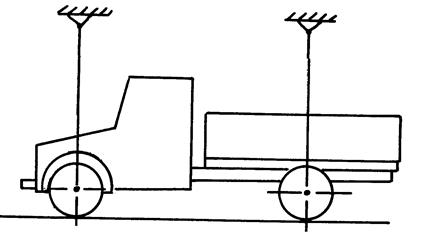 Так, если длина подвесов – L (м), расстояние между подвесами – a (м), вес автомобиля – Gа (Н, кг×м/с2), период колебаний вокруг вертикальной оси – Т (с), то для подвеса на трех канатах – один спереди, два сзади – момент инерции автомобиля Jz (кг×м2) вокруг вертикальной оси может быть найден с помощью зависимости [ ]:
Так, если длина подвесов – L (м), расстояние между подвесами – a (м), вес автомобиля – Gа (Н, кг×м/с2), период колебаний вокруг вертикальной оси – Т (с), то для подвеса на трех канатах – один спереди, два сзади – момент инерции автомобиля Jz (кг×м2) вокруг вертикальной оси может быть найден с помощью зависимости [ ]:
Jz = 84,44×10-6 × 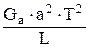 .
.
Рис. 33. Определение момента инерции
автомобиля вокруг вертикальной оси
Таким же образом могут быть определены моменты инерции колес автомобиля, существенно влияющие на разгон и торможение автомобиля.
Силы сопротивления движению автомобиля
Сопротивление движению автомобиля складывается из следующих сил:
1. Сопротивление качению колес – Pf .
2. Сопротивление подъема – Ph .
3. Инерции автомобиля – Рj
4. Сопротивление воздуха – Pw .
 Сопротивление качению колес автомобиля может быть найдено путем сложения сопротивлений качению всех его колес или умножением веса автомобиля на коэффициент сопротивления качению f. Значения f для различных дорог приведены в табл. 2.
Сопротивление качению колес автомобиля может быть найдено путем сложения сопротивлений качению всех его колес или умножением веса автомобиля на коэффициент сопротивления качению f. Значения f для различных дорог приведены в табл. 2.
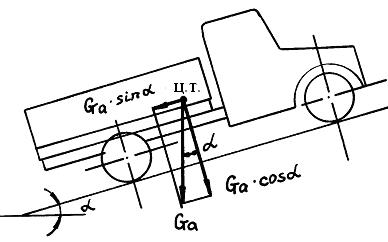
Сопротивление качению колес на дороге с уклоном может быть определено с помощью рис. 34, где показано разложение вектора Рис. 34. Разложение вектора силы тяжести силы тяжести автомобиля по автомобиля по двум направлениям на две плоскости: параллель-
ную дороги и перепендику-
лярную к ней.
Сила сопротивления качению колес автомобиля на подъеме равна:
Рf = Ga cos a × f ,
где Ga cos a – проекция вектора силы тяжести на плоскость, перпендикулярную
поверхности дороги.
Сопротивления подъема Рh есть проекция вектора силы тяжести автомобиля на плоскость, параллельную дорожной поверхности:
Рh = Ga sin a .
Общее сопротивление дороги на подъеме равно Рy = Рf + Рh , что можно записать как
Рy = Gа ×(f cos a + sin a ) = Gа ×y , (17)
где y – коэффициент обшего дорожного сопротивления.
Сила инерции автомобиля Рj складывается из следующих составляющих
Рj = Рja + Рjk + Рjд , (26)
где Рj – сила инерции автомобиля; Рjk – сила инерции колес автомоюиля; Рjд – приведенная сила инерции вращающихся деталей двигателя.
Pj = 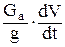 +
+ 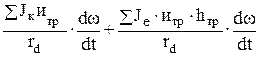 , (27)
, (27)
где SJk – сумма моментов инерции колес; SJе – сумма моментов инерции вращающихся деталей двигателя; dwk/dt – угловое ускорение колес; dwe/dt – угловое ускорение деталей двигателя; итр – передаточное чтисло трансмиссии; hтр – кпд трансмиссии. Остальные обозначения использовались ранее.
Исходя из того, что V = w×r, (где V – окружная скорость; w – угловая скорость; r – радиус колеса), в уравнение (27) вместо dwк /dt и dwе /dt подставляем выражения
dwк /dt = dV/dt ×1/rк и dwк /dt = dwе /dt × итр = dV/dt × итр/rк ,
получим
Pj = 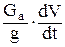 +
+ 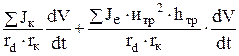 =
=
= 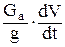 ×
× 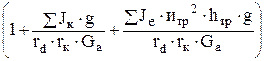 . (28)
. (28)
Выражение в скобках обозначим d. Оно называется к о э ф ф и ц и е н т о м у ч е т а в р а щ а ю щ и х с я м а с с автомобиля. Сила инерции автомобиля с использованием этого коэффициента может быть определена:
Pj = 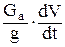 × d .
× d .
Коэффициент учета вращающихся масс находится обычно по эмпирической зависимости, предложенной акад. Чудаковым Е.А. [ ].
d = 1 + 0,03...0,05 + 0,04 икп2 × ирк2 , (29)
где икп – передаточное число передачи в коробке передач; ирк – передаточное число передачи в раздаточной коробке.
Численное значение коэффициента учета вращающихся масс d на первой передаче в коробке передач и низшей передаче в раздаточной коробке полноприводных автомобилей достигает 6,5...7, а неполноприводных, в которых отсутствует раздаточная коробка, d = 1,7...2,5. На последней передаче в коробке передач и высшей передаче в раздаточной коробке d = 1,06...1,13.
Сопротивление воздуха является основной силой сопротивления для автомобиля, движущегося с высокой скоростью. При скорости 80...90 км/ч сопротивление воздуха для легковых автомобилей становится равным сопротивлению качению колес на горизонтальной асфальтированной дороге, а далее – значительно превышает его. Близкие к этим величинам показатели и грузовых автомобилей. Снижению сопротивления воздуха поэтому уделяется большое внимание особенно для легковых автомобилей, скорости которых, как правило, значительно выше 90 км/ч..
Сопротивление воздуха движению тела в диапазоне скоростей от 1 м/с до 330 м/с (скорость звука) зависит от скорости в квадрате, а при скорости выше звуковой – в кубе. Т.е. для реальных скоростей автомобиля зависимость силы сопротивление воздуха от скорости – квадратичная:
Рw = 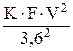 , (18)
, (18)
где Рw – сила сопротивление воздуха, Н; К – коэффициент сопротивления воздуха, Н×с2 /м4; F – наибольшая поперечная (лобовая) площадь автомобиля, м2; V– скорость автомобиля, км/ч.
Приближенно лобовую площадь F можно определить по следующим зависимостям: для грузовых – F = B ×H , для легковых – F = 0,78 B1×Н, где B – колея автомобиля. Самое малое сопротивление воздуха имеет падающая капля воды, её наибольшая площадь сечения находится на расстоянии 1/3 от преднего конца.
Численные значения К и F приведены в табл. 6.
Таблица 6
| Автомобили | F, м2 | K, Н×с2/м4 |
| Легковые Грузовые Автобусы | 1,5...2,5 3...5 4,5...6,5 | 0,2...0,35 0,6...0,7 0,25...0,4 |
.
Лобовая площадь равна: ВАЗ-2106 – 1,74 м2, М-2141 – 1,887 м2, ГАЗ-3110 – 2,277 м2 , Газель – 3,25 м2, ГАЗ-52 – 3,3 м2, ГАЗ-53 – 3,84 м2, ЗИЛ-130 – 4,9 м2, КАМАЗ-5320 – 6,85 м2 , МАЗ-5335 – 6,4 м2, ЛИАЗ-677 – 6,53 м2.
С учетом угла натекания на автомобиль воздушного потока, силы действия потока по направлениям осей координат, исходящим из центра тяжести автомобиля, определяются как [10]:
Рw = Сx × 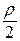 × F ×V2 , (19) где Сx – коэффициент лобового сопротивления, величина безразмерная; r –плотность воздуха (1,25 кг/м3 при давлении 760 мм ртутного столба и 18оС, ГОСТ 4401-81).
× F ×V2 , (19) где Сx – коэффициент лобового сопротивления, величина безразмерная; r –плотность воздуха (1,25 кг/м3 при давлении 760 мм ртутного столба и 18оС, ГОСТ 4401-81).
Под углом натекания воздушного потока в плоскости, параллельной плоскости дороги, понимается угол между направлением движения автомобиля и геометрической суммой скорости воздушного потока и скорости движения автомобиля. То же в вертикальной плоскости называется углом атаки. Обычно угол натекания не более 30о.
Кроме продольной силы от воздушного потока на автомобиль действует также боковая Ру и подъемная Рz силы. При этом боковая сила оценивается коэффициентом боковой силы Сy, подъемная сила – коэффициентом подъемной силы Сz . Коэффициент полной аэродинамической силы Сw равен
____________
Cw = Ö Cx2+ Cy2 + Cz2 . (20)
Наибольшее значение для практической оценки влияния сопротивления воздуха имеет коэффициент Cx, который обычно используется для xарактеристики обтекаемости автомобиля, равен:
Cx = 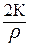 = 1,63К ,
= 1,63К ,
где К – коэффициент сопротивления воздуха.
Выражение 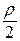 ×V2 в приведенной выше формуле для определения Рw называется скоростным напором воздушного потока, действующего на автомобиль и обозначается через q :
×V2 в приведенной выше формуле для определения Рw называется скоростным напором воздушного потока, действующего на автомобиль и обозначается через q :
q = 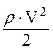 . (21)
. (21)
Полная аэродинамическая сила может быть найдена по выражению
Рw = Cw × F ×q . (22)
Тогда
Сx = 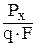 ; Cy =
; Cy = 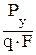 ; Сz =
; Сz = 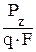 .
.
Значения коэффициентов Сxавтомобилей: ВАЗ-2106 – 0,509; ВАЗ-2108 и ВАЗ-2109 – 0,38; ЗАЗ-1102 – 0,37; М-2141 – 0,478; ГАЗ-24 – 0,48; ГАЗ-33029 – 0,413; ГАЗ-13 – 0,502; РАФ-2203 – 0,439; ПАЗ-652 – 0,376; ЛИАЗ-677 – 0,734; ГАЗ-53 – 0,965; ЗИЛ-130 – 0,805; КАМАЗ-5320 – 0,673; МАЗ-5335 – 0,75.
Атомиобиль с хорошо отработанной формой кузова Мерседес кл. Е имеет Сx= 0.27… 0,29. Для легковых спортивных автомобилей Сx= 0,14...0,2, например, Форд Проба – 0,14, Мицубиси ХСР – 0,2. Наиболее обтекаемую форму имеет падающая капля, для неё Сх = 0,05..
Действующий под углом натекания воздушный поток вызывает поворот автомобиля вокруг осей X, У, Z . Практическое значение имеет лишь поворот вокруг оси Z, который влияет на курсовую устойчивость автомобиля. Действие момента вокруг оси Z оценивается коэффициентом поворачивающего момента.
Поворачивающие автомобиль моменты вокруг осей Z, Х и У определяются
Мz = mz × q × F × B, Мx = mx ×q ×F×B и My = my ×q ×F ×L , (23)
где mх, my, mz – коэффициенты поворачивающего момента вокруг осей Z, Х и У; q – скоростной напор; F – лобовая площадь; B – ширина автомобиля, L – длина автомобиля.
Зависимость коэффициентов Сх, Су Сz и mх, my, mz в от угла натекания воздушного потока показаны на рис. 35, 36, 37
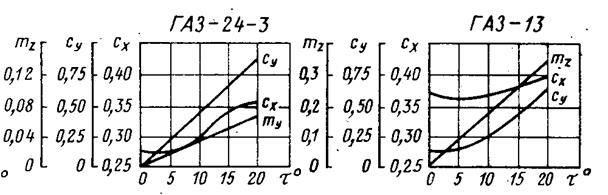
Рис. 35. Зависимость коэффициентов Сx, Cy, Сz и mz от угла натекания воздушного потока t о для легковых автомобилей ГАЗ-24-3 и ГАЗ-13
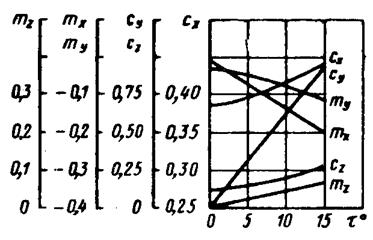
Рис. 36. Зависимость коэффициентов Сx, Cy, Сz и mх, my, mz от угла натекания воздушного потока t о для грузового автомобиля ЗИЛ-130
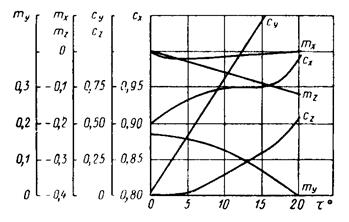
Рис. 37. Зависимость коэффициентов Сx, Cy, Сz и mх, my, mх от угла натекания воздушного потока t о для автобуса ПАЗ-652
Полный аэродинамический момент Mw выражается
Мw = mw ×q ×F × B ,
где mw – коэффициент полного аэродинамического момента. Он определяется
___________________
mw = Ö mx2 + (my × B/L + mz2 ) . (24)
Численные значения поворачивающего момента, подъемной силы и лобового cопротивления при скорости 100 км/ч и угле натекания 20o автомобилей ГАЗ-21 и ГАЗ-24 "Волга" приведены в табл. 5.
Таблица 7
| Автомобили | Поворачивающий момент, Н×м | Подъемная сила, Н | Лобовое сопротивление, Н |
| ГАЗ-21 ГАЗ-24 |
Приведенные сопротиления воздуха определялись на уровне моря. На высоте в горных районах сопротивление снижается. Так мощность сопротивления воздуха движению автомобиля ГАЗ-24 при скорости 80 км/ч на уровне моря равно 8 л.с., а на высоте 2500 м – 5,5 л.с.
С целью снижения сопротивления воздуха форма кузова легкового автомобиля тщательно отрабатывается в специальном устройстве – аэродинамической трубе, где воздушный поток создается с помощью вентиляторов. Чтобы расход электроэнергии на привод вентиляторов был минимальный, труба делается замкнутой.
Испытания в аэродинамической трубе ведутся на автомобилях в натуральную величину или на уменьшенных моделях с сохранением критерия подобия – числа Рейнольдса
R = 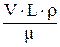 =
= 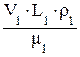 , (25)
, (25)
где L – длина автомобиля; L1 – длина модели; V – скорость воздушного потока при испытаниях автомобиля; V1 – скорость воздушного потока при испытаниях модели; r – плотность воздуха (1,22 кг/м3); m – коэффициент вязкости воздуха (1,82 ×10–6 кг×с/м при давлении 760 мм ртутного столба и 18o C, ГОСТ 4401-81); r1 и m1 – плотность и коэффициент вязкости воздуха при испытаниях модели.
Если r и m принять без изменений, то V×L = V1×L1. Таким образом, чем меньше длина модели, тем больше должна быть скорость воздушного потока.
Дата добавления: 2020-06-09; просмотров: 1575;











