Характеристики двухфазных систем жидкость – пар

Если система состоит из К = 2 и имеются две фазы Ф = 2, то число степеней свободы:

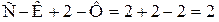
Следовательно, из трех независимых переменных определяющих состояние системы t, р, с можно выбрать два, третья переменная уже не будет произвольной.

В связи с этим для физико – химической характеристики бинарных систем жидкость – пар удобно пользоваться фазовыми диаграммами.

Если t = const построить зависимость р – х.

Если р = const построить зависимость температур кипения жидкости и конденсации паров от составов жидкой и паровой фаз (t – х – y).

Если t = const, р = const можно найти зависимость между равновесными составами фаз (y – х).

Классификация бинарных смесей. В зависимости от взаимной растворимости компонентов различают: 1) жидкости с неограниченной взаимной растворимостью; 2) взаимно нерастворимые; 3) ограниченно растворимые друг в друге.

Жидкости с неограниченной взаимной растворимостью в свою очередь делятся на идеальные и неидеальные смеси.

Идеальные растворы следуют законам Рауля и Дальтона.

При смешивании компонентов идеального раствора тепловой эффект отсутствует и объем смеси практически не изменяется.

Закон Рауля:

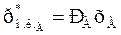
где р_А – давление насыщенного пара низкокипящего компонента А.

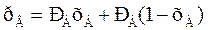
где х_В – мольная доля компонента В.

Закон Дальтона:

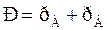
При t = const парциальное давление компонентов, а также общее давление, находится в линейной зависимости от мольной доли низкокипящего компонента.

Построим изотермы парциальных давлений компонентов и общего давления для идеальных растворов (р – х).

t = const прямые ОВ и СА изображают изменение парциальных давлений компонентов (р_А и р_В), а АВ – изменение общего давления над раствором. Вертикальные отрезки СВ и ОА – выражают давления насыщенных паров чистых компонентов (Р_А и Р_В).

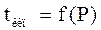
Для ее определения строят по значениям давлений насыщенных паров чистых компонентов изотермы А₁В₁ и А₂В₂, которые выражают общее давление паров при t₁и t₂.

МN – горизонтальная прямая, соответствующая внешнему давлению и получаем точку D на пересечении АВ и MN. Смесь состава х_А кипит при температуре в точке D.

Для построения зависимости температур кипения и конденсации от состава фаз (t – х – y) на оси ординат откладывают температуры кипения t₁, t₂, t₃, соответствующие составам жидких смесей х₁, х₂, х₂ , отложенные на оси абсцисс. Через полученные точки и точки t_В и t_А, соответствующие температурам кипения чистых компонентов проводим линию кипения АА₁А₂А₃В.

Затем на оси абсцисс откладывают определенные по закону Рауля равновесные составы паров 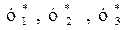и проводят из соответствующих им точек прямые до пересечения с изотермами t₁, t₂, t₃ . Соединив точки АВВ₁В₂В₃ получаем линию конденсации.

Диаграмма равновесия пар – жидкость (y – х)

На диаграмму наносится линия равновесия, выражающая зависимость между равновесными составами (по низкокипящему компоненту – НК), жидкой х и паровой у фаз.

С жидкостью, состоящей из чистого НК, находится в равновесии пар, содержащий 100% НК. Линия равновесия и диагональ квадрата ограничивают область взаимного существование двух фаз. Выпуклость линии равновесия зависит от отношения теплот испарения компонентов 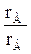. При 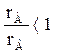с увеличением давления кривая равновесия становится менее выпуклой.

Уравнение равновесия:

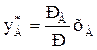
для идеального раствора:

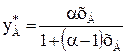
где 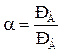– относительная летучесть компонентов смеси, равная отношению давлений паров чистых компонентов при одинаковом внешнем давлении.

Взаимное положение кривых на фазовых диаграммах t – х – y определяется первым законом Коновалова: пар обогащается тем компонентом, при добавлении которого к жидкости повышается давление над ней или снижается ее температура кипения.

Закон Коновалова дополняется законом Вревского: при повышении температуры смеси испаряется преимущественно тот компонент, парциальная мольная температура испарения которого больше, что обуславливает относительно большее содержание этого компонента в паре (этот закон выражает общий принцип Ле – Шателье).

++++++++++++++ +++++++++++++++++++ +++++++++++++

Значения коэффициента сопротивления λ определяются по эмпирическим уравнениям:

при Re_г < 40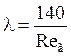

при Re_г > 40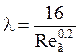

где 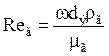– критерий Рейнольдса для газа (ρ_г и μ_г плотность и вязкость газа).

Коэффициент смачиваемости – отношение удельной смоченной поверхности ко всей удельной поверхности:

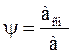
Зависимость гидравлического сопротивления насадки от скорости газа

в колонне

I – для сухой насадки; II – для орошаемой насадки; 1 – точка торможения; 2 – точка подвисания; 3 – точка инверсии; 4 – точка захлебывания; А – пленочный режим; В – промежуточный режим; С – турбуляционный режим; D – режим эмульгирования.

Гидродинамические режимы работы тарелок:

1. пузырьковый – поверхность контакта фаз на тарелке не велика;

2.пенный – поверхность контакта фаз максимальна. Разрушается вследствие сопротивления барботажного слоя. Газо – жидкостная дисперсионная система – пена.

3. струйный (инжекционный) режим. Струя не разрушается и при выходе на поверхность барботажного слоя образует большое количество брызг – поверхность контакта резко уменьшается.

++++++++++++++ +++++++++++++++++++ +++++++++++++

Уравнения рабочих линий

Воспользуемся общим для всех массообменных процессов уравнением концентрации на верхнем конце колонны:

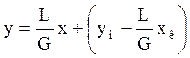(1)

Применяя это уравнение к процессу ректификации, выразим все входящие в него величины в мольных единицах.

Укрепляющая часть колонны. Количество жидкости (флегмы), стекающее по этой части колонны:

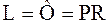
где 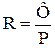– флегмовое число.

Количество паров, поднимающихся по колонне:

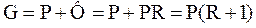
Для верхнего конца колонны: состав паров y_G = y_P. Допускаем у_Р = х_Р , следовательно у_Н = х_Р

В том же сечении колонны состав жидкости (флегмы), поступающей из дефлегматора, х_Ф = х_Р , т.е. х_К = х_Р . Подставив в уравнение (1) получим:

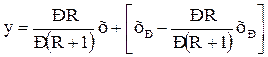
откуда

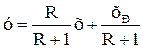
где 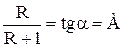– тангенс угла наклона рабочей линии к оси абсцисс;

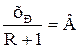– отрезок, отсекаемый рабочей линией на оси ординат.

Исчерпывающая часть. Обозначим количество питания, приходящегося на 1 кмоль дистиллята, через 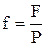, то 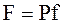и количество жидкости, стекающей по исчерпывающей части колонны:

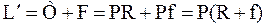
Количество пара, проходящего через нижнюю часть, равно количеству пара, поднимающегося по верхней части:

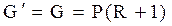
Для низа колонны 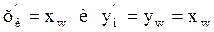, получим:

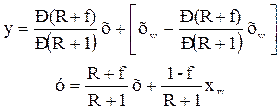
где 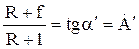– тангенс угла наклона рабочей линии к оси ординат;

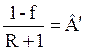– отрезок, отсекаемый рабочей линией на оси абсцисс.

Допущение о равенстве составов пара и жидкости на концах колонны. Построение рабочих линий у – х.

Расчет минимального флегмового числа:

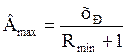
R уменьшается – В увеличивается; R увеличивается – В уменьшается;

А = А^′ = 1; В = В^′ = 0; R = ∞.

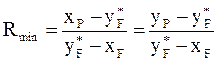
R = ∞, Р = 0, расход греющего пара в кипятильнике наибольший; R_min рабочая линия пересекается с линией равновесия в точке пересечения движущая сила равна 0→ бесконечно большое число ступеней, бесконечно большая высота аппарата → расход греющего пара min.

С увеличением R высота аппарата уменьшается, а расход греющего пара возрастает.

Расчет действительного флегмового числа

С увеличением R возрастает движущая сила процесса и уменьшается необходимое число теоретических и, соответственно, действительных ступеней. В итоге, при некотором флегмовом числе рабочий объем колонны станет минимальным и, следовательно, будет минимальна стоимость.

1 – эксплуатационные расходы; 2 – капитальные затраты; 3 – общие затраты на ректификацию.