Расчет насадочного абсорбера
1. Диаметр находят по уравнению расхода:

где VС – секундный расход газа, м3/сек;
ωГ – фиктивная скорость газа, м/сек;
ωГ = 0,8ω0 (ω0 – скорость газа при захлебывании колонны).
Скорость газа при наличии «подвисания» жидкости рассчитывают по формуле:
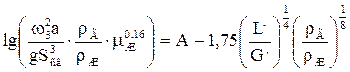
где а – удельная поверхность насадки м2/м3;
Sсв – свободный объем насадки м2/м2;
А = -0,073 – постоянная для паро – жидкостной смеси;
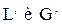 – расходы жидкости и газа, кг/сек.
– расходы жидкости и газа, кг/сек.
Высота насадки:
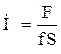
где 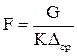 – площадь поверхности контакта.
– площадь поверхности контакта.
2. Полагая, что абсорбер работает в пленочном режиме. Коэффициент массоотдачи в газовой фазе можно определить по уравнению:
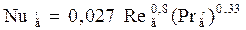
Коэффициент массоотдачи в жидкой фазе:
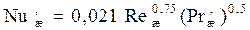
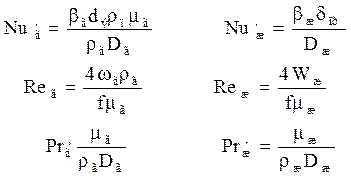
где 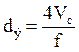 – эквивалентный диаметр насадки, м;
– эквивалентный диаметр насадки, м;
ρп – среднее парциальное давление инертного газа в абсорбере, мм.рт.ст.;
μг – молекулярная масса смеси газов;
Dг , Dж – коэффициент диффузии в газе и жидкости, м2/ч;
Wж – количество жидкости, кг/(м2·с);
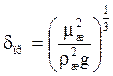 – приведенная толщина пленки жидкости.
– приведенная толщина пленки жидкости.
3. Высоту насадки определяется по числу единиц переноса:
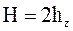
2 – число единиц переноса (ЧЕП);
hz – ВЕП.
или же
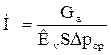
где Gа – количество абсорбируемого газа, кмоль/ч;
КV – объемный коэффициент массопередачи.
4. Гидравлическое сопротивление абсорбера
Для сухой насадки:
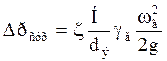
где γг – удельный вес газа в кг/м3
Выразим скорость газа через приведенную скорость ωпр и свободный объем насадки Vс
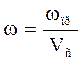
тогда потери давление на 1м высоты насадки можно определить:
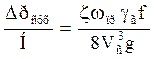
Коэффициент сопротивления для насадки из колец:
при Reг < 40 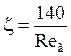
при Reг > 40 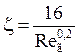
при регулярной насадки:
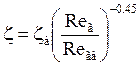
где Reга – значение Re – соответствующее переходу в автомодельный режим:
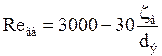
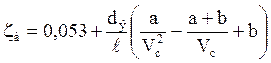
где L – высота ряда насадки, м;
а и b – постоянные (а = 4,2 и b = 3,9 – для колец и блоков; а = 0,52 и
b = - 0,67 – для хордовой насадки).
Сопротивление орошаемой насадки:
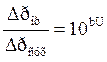
где b – постоянная;
U – плотность орошения.
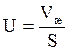
где Vж – объемный расход жидкости.
| b | |||||
| dколец | до 12,5 | до 19 | 32-38 | для спиральных колец |
При малых плотностях орошения:
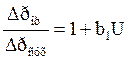
где b1 = 216 для хордовой насадки и колец в навал;
b = 144 для регулярной насадки.
Для тарельчатых абсорберов
полное сопротивление тарелки, складывается из:
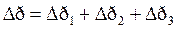
где 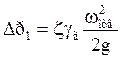 – сопротивление сухой тарелки;
– сопротивление сухой тарелки;
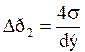 – сопротивление газожидкостного слоя;
– сопротивление газожидкостного слоя;
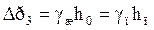 – сопротивление, обусловленное силами поверхностного натяжения;
– сопротивление, обусловленное силами поверхностного натяжения;
γж и γп – удельный вес жидкости и пены;
h0 и hп – высота слоев жидкости и пены.
Средняя движущая сила и число единиц переноса
Интеграл в знаменателе называется числом единиц переноса
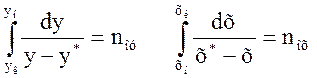
 (W)
(W)
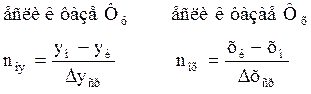

Число единиц переноса характеризует изменение рабочей концентрации фазы, приходящееся на единицу движущей силы.
Или же можно сказать, что одну единицу переноса можно рассматривать как участок аппарата, для которого изменение концентрации одной из фаз равно средней движущей силе на этом участке.
Выразим общее число единиц переноса nох и nоy в функции от числа единиц переноса в фазах. Для этого вместо уравнения массопередачи рассмотрим уравнение массоотдачи, т.е. заменим Кx и Кy на bх и by , а равновесные концентрации y* и х* на концентрации по поверхности раздела хгр, yгр.
Представим уравнение массоотдачи в виде:
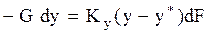 (А)
(А)
Тогда уравнение массоотдачи запишем в виде:
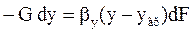 (Б)
(Б)
где G – расход фазы Фy;
y – концентрация этой фазы.
После интегрирования уравнения (Б) по всей поверхности массопереноса получим число единиц переноса в фазе Фy:
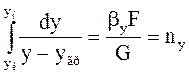
Аналогично число единиц переноса для фазы Фх:
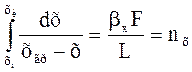
где L – расход фазы Фх
Разделяя переменные и интегрируя уравнение (А) с учетом выражения (W) найдем зависимость между числом единиц переноса nоy и коэффициентом Кy:
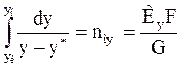
Уравнения аддитивности фазовых сопротивлений:
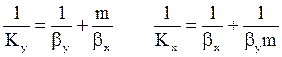

Отсюда, используя правило аддитивности фазовых сопротивлений получим:
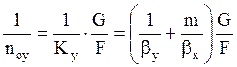
Теперь вместе коэффициентов bх и by подставим полученные значения nх и ny, т.е. установим связь между nоy, ny и nх:
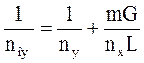
Величина 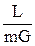 называется фактором процесса массопередачи.
называется фактором процесса массопередачи.
Обозначим для кратности это выражение А, получим:
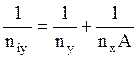
 Аналогично для фазы Фх можно вывести:
Аналогично для фазы Фх можно вывести:
Из подобия ΔАСD и ΔАВЕ следует, что 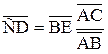 , по построению
, по построению 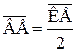 и
и 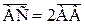 , откуда:
, откуда:
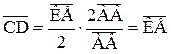
Таким образом, изменение рабочей концентрации на данном участке (отрезок 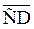 ) равно средней движущей силе на этом участке (отрезок
) равно средней движущей силе на этом участке (отрезок 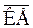 ) и следовательно, «ступенька» изображает одну единицу переноса.
) и следовательно, «ступенька» изображает одну единицу переноса.
Высота единиц переноса (ВЕП) массопередачи происходит из фазы Фy в фазу Фх, движущая сила выражается в концентрациях фазы Фy. Тогда количество вещества, переходящего из фазы в фазу составит:
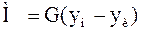 (А)
(А)
где G – расход фазы;
yн и yк – начальная и конечная концентрация фазы Фy.
Вместе с тем величина М может быть определена по уравнению массопередачи через объемный коэффициент массопередачи:
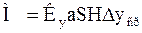 (Б)
(Б)
где Куа – объемный коэффициент массопередачи, принимаемый постоянным по высоте аппарата;
S – площадь поперечного сечения аппарата;
Н – рабочая высота аппарата.
Приравняв выражение (А) и (Б) получим:
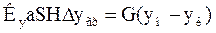
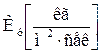
Тогда рабочая высота аппарата:
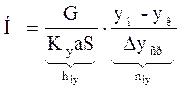
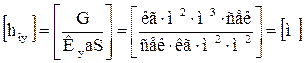
и носит название высоты единицы переноса (ВЕП).
Аналогично для фазы Фх:
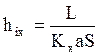
Высота единицы переноса соответствует высоте аппарата, эквивалентной одной единице переноса.
Величина ВЕП обратно пропорциональна объемному коэффициенту массопередачи. Следовательно, чем выше интенсивность массопередачи в аппарате, тем меньше в нем величина ВЕП.
Объемные коэффициенты массоотдачи и массопередачи
В барботажных аппаратах поверхность контакта фаз – это совокупность поверхностей: брызг, пены и пузырей.
В насадочных аппаратах это некоторая «активная» часть геометрической поверхности насадки, смачиваемая жидкостью. Поэтому коэффициенты массоотдачи и массопередачи относят к рабочему объему аппарата V, который связан с поверхностью контакта зависимостью:
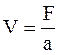
где а – удельная поверхность контакта фаз, т.е. поверхность, отнесенная к единице рабочего объема аппарата.
Подставив в выражение:
для фазы Фy
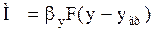
для фазы Фх
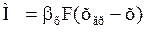
Величину 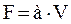 получим:
получим:
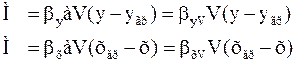
Аналогична подстановка:
для фазы Фy
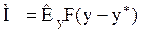
для фазы Фх
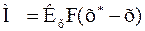
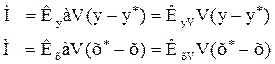
Величины 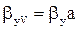 и
и 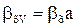 называются объемными коэффициентами массоотдачи, а величины
называются объемными коэффициентами массоотдачи, а величины 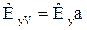 и
и 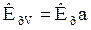 объемными коэффициентами массопередачи.
объемными коэффициентами массопередачи.
Тогда если 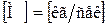 , а
, а 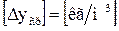 ,
,
то
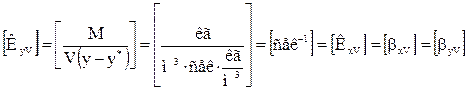
Коэффициент извлечения (обогащения)
Эффективность работы массообменных аппаратов можно охарактеризовать степенью извлечения распределяемого компонента.

G = const; L = const; у* = f (х) – линия равновесия.
При противотоке количество распределяемого компонента из фазы Фy 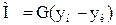 . Тогда предельно возможное поглощение этого компонента фазой Фх может быть достигнуто в том случае, если при противотоке фаза, отдающая распределяемый компонент М (фаза Фy) на выходе из аппарата будет находиться в равновесии с поступающей в него жидкостью (концентрацией хн), т.е. будет иметь концентрацию
. Тогда предельно возможное поглощение этого компонента фазой Фх может быть достигнуто в том случае, если при противотоке фаза, отдающая распределяемый компонент М (фаза Фy) на выходе из аппарата будет находиться в равновесии с поступающей в него жидкостью (концентрацией хн), т.е. будет иметь концентрацию 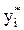 . Соответственно, максимально возможное увеличение
. Соответственно, максимально возможное увеличение 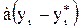 .
.
Отношение действительного количества компонента, перешедшего в аппарате из фазы в фазу, к тому количеству, которое максимально может перейти, является важной характеристикой массообменного аппарата и носит название коэффициента извлечения:
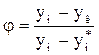
В том случае рабочая и равновесная линии – прямые, а уравнение линии равновесия 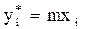 . Тогда:
. Тогда:
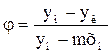
Дата добавления: 2016-06-29; просмотров: 2325;











