Построение касательных и нормалей к плоским кривым

Для проведения касательной к кривой необходимо задать уравнение кривой в каком либо виде: Y=F(x); или F1(x, y)=0; или X=Fx(t); Y=Fy(t); и координаты точки на кривой (xi, yi).

Уравнение касательной к кривой имеет вид:

(x-xi)*dY/dx =(y-yi);или(x-xi)*dFy/dt = (y-yi)*dFx/dt;

где dY/dx = dF(x)/dx = - (¶F1(x, y)/¶x)/(¶F1(x, y)/¶y);

Уравнение нормали к кривой имеет вид:

(x-xi) = -(y-yi)*dY/dx;или(x-xi)*dFx/dt = -(y-yi)*dFy/dt;

Пусть уравнение кривой имеет вид: X=A*cos(t); Y=B*sin(t); - эллипс. Алгоритм построения касательной к кривой в расчетной области X_Min<=x<=X_Max , Y_Min<=y<=Y_Max следующий.

1) Находим производные dFx/dt=-A*sin(t); dFy/dt=B*cos(t).

2) В области изменения параметра "t" задаем ti и определяем координаты точки Xi, Yi и производные dXi= (dFx/dt)_i, dYi= (dFy/dt)_i в точке "ti".

3) Находим точки "1" и "2" пересечения касательной с границами расчетной области:

при dXi<>0 полагаем x1=x_Min и находим y1=(x1-xi)*dYi/dXi + yi;

если y1< y_Min, то y1=y_Min и определяем x1= (y1-yi)*dXi/dYi + xi;

если y1> y_Max, то y1=y_Max и определяем x1= (y1-yi)*dXi/dYi + xi;

аналогично, при dXi<>0 полагаем x2=x_Max и находим y2 по приведенной выше схеме с корректировкой значений y2 и x2.

При dXi=0 полагаем x1=xi и y1=y_Max и x2=xi и y2=y_Min.

4) Через точки "1" и "2" проводим прямую.

L   Yi L     Xi

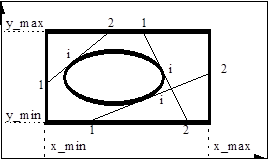
Несколько проще алгоритм построения касательной постоянной длины "2*L" к плоской кривой. В этом случае:

при dXi<>0 находим alf=arctg(dY/dx)_i; иначе alf=90⁰; и определяем:

x1 = xi + L*cos(alf); y1 = yi + L*sin(alf);

x2 = xi - L*cos(alf); y2 = yi - L*sin(alf);

При построении нормали используется уравнение нормали к кривой и приведенные выше алгоритмы.