Устойчивость откосов и склонов

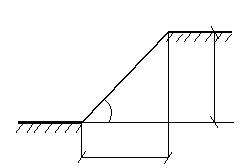
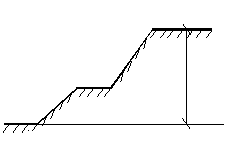
Откос – необходимый элемент всех сооружений из грунта – насыпей, дамб, плотин и выемок, карьеров, котлованов. Природный откос называется склоном. Элементы простого откоса: высота Н, заложение В, угол наклона α, бровка т. А (рис. 4.4, а). Откосы могут иметь сложное очертание с различными углами наклона по высоте и горизонтальными площадками (бермы, рис. 4.4 б). Крутизна откоса задается в виде 1 : m, где m=B/H. Например, при α = 45˚ m = 1; при α= π/2, m = 0 имеем вертикальной откос (рис. 4.4, в).

А В α а)	б)
в) Рис. 4.4.

В некоторых случаях устойчивость откосов можно оценить из условия предельного равновесия. Пусть, например, в откосе из песчаного грунта с углом внутреннего трения φ призма АВД, отсеченная плоскостью под углом α, находится в состоянии предельного равновесия (рис. 4.5).

Тогда вес призмы Q можно разложить на две силы: сдвигающую Т_сдв, действующую в плоскости сдвига и нормальную N, обуславливающую появление удерживающей силы Т_уд. Из схемы очевидно:

Т_сдв= Q·Sinα; Т_уд.= N· tgφ = Q·Cosα· tgφ (4.9)

Приравнивая, получаем УПР для песчаного откоса (при С = 0): α = φ

Угол α, образуемый песком при свободной отсыпке его на горизонтальную плоскость, называется углом естественного откоса.

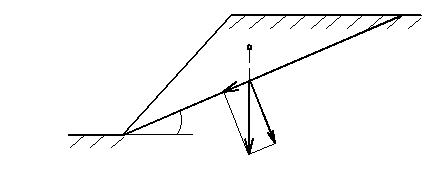
Рис. 4.5.

Соответственно условием устойчивости такого откоса будет α < φ, а степень устойчивости можно оценить коэффициентом:

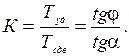(4.10)

Аналогично можно установить предельную высоту вертикального откоса (рис. 4.4, в). Считаем (в запас надежности), что обрушение откоса может последовать за разрушением грунта в наиболее напряженной точке откоса. Напряжения в ней равны: σ₁= γ h_кр; σ₃= 0.

Подставляя их в УПР (2.16) и разрешая полученное выражение относительно h_кр, получаем:

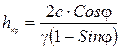(4.11)

Задачи об устойчивости откосов решаются строго на основе системы уравнений ТПР (4.6; 4.7). Известно два варианта таких задач:

1) Задано очертание откоса и характеристики грунта φ, с, γ. Определяется нагрузка на поверхности, при которой грунт находится в предельном равновесии.

2) Задана интенсивность нагрузки на верхней горизонтальной поверхности. Требуется установить такое очертание откоса, при котором грунт будет в предельном равновесии (это задача об очертании равноустойчивого откоса).

На практике для слоистых откосов, сложенных песчаными и пылевато-глинистыми грунтами, расчет устойчивости часто проводится методом круглоцилиндрической поверхности скольжения (методом отсеков).

Предполагается, что потеря устойчивости откоса может произойти в результате вращения части массива грунта относительно т. О (рис. 4.6).

Кривая скольжения принимается дугой окружности с радиусом R и центром в т. О. Коэффициент устойчивости здесь выражается отношением моментов удерживающих и сдвигающих сил:

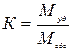. (4.12)

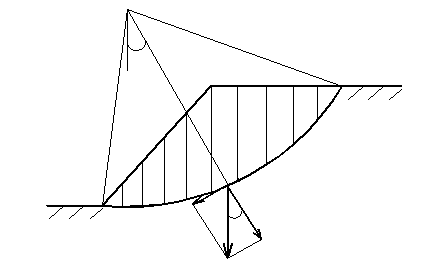
Рис. 4.6.

Для их определения массив, выделенный поверхностью скольжения, разбивается на отдельные отсеки и вычисляется вес каждого отсека Q_i. Если на поверхности данного отсека задана нагрузка, она также включается в Q_i. Силы Q_i считаются приложенными к основанию отсека и раскладываются на нормальную N_i и касательную Т_i составляющие к дуге скольжения:

N_i =Q_i ·Cos α_i ; Т_i = Q_i ·Sin α_i .

Моменты сил будут равны:

;

,

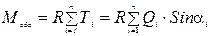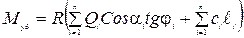где 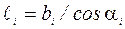- длина дуги в пределах каждого отсека.

Отношение моментов по (4.12) дает формулу коэффициента устойчивости:

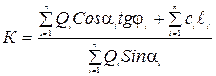. (4.13)

Смысл коэффициента устойчивости такой: при К > 1 откос устойчив; при К < 1 не устойчив, а при К = 1 откос находится в предельном (т.е. неустойчивом) равновесии, что также недопустимо. Но самое главное – условие К>1 должно выполняться для наименьшего коэффициента устойчивости, рассчитанного для опаснейшей поверхности скольжения. Они устанавливаются проведением серии расчетов для различных положений центра и значений радиуса R. Нормативные коэффициенты устойчивости (надежности) назначаются при проектировании больше единицы в пределах 1,2…1,5. Запас надежности необходим из-за приближенности расчетной схемы, неоднородности грунтов, неточности определения их характеристик и других факторов.