Методы нахождения центра тяжести.

Метод симметрии.

Покажем, что если однородное тело имеет плоскость, ось или центр материальной симметрии, то его центр тяжести находится соответственно в плоскости, на оси или
в центре симметрии.

а. Пусть тело симметрично относительно плоскости Оху

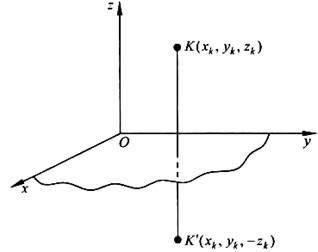
Тогда вследствие симметрии каждому элементу К тела объемом 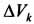( 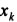, , 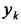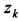) будет соответствовать элемент К' того же объема с координатами ( 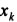, ,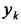- 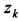). Поэтому статический момент объема 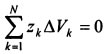и координата 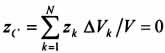. Следовательно, центр тяжести тела будет лежать в плоскости симметрии Оху.

б. Пусть тело симметрично относительно оси Oz.

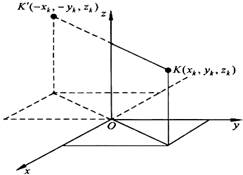
Тогда всякому элементу К тела объемом 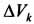с координатами ( 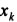, , 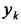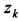) будет соответствовать такой же по объему элемент К', расположенный симметрично относительно оси Oz и имеющий координаты (- 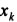,- , 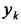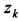). Поэтому статические моменты 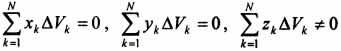и, следовательно, координаты 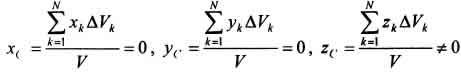. Таким образом, центр тяжести будет находится на оси симметрии.

в. Пусть тело имеет центр симметрии, который примем за начало координат. Тогда всякой частице тела объемом 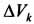, определяемой радиус-вектором rк, будет соответствовать частица такого же объема с радиус-вектором (-rк), симметричная ей относительно центра О. Поэтому 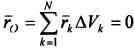. Следовательно, центр тяжести будет находиться в центре симметрии. Например, центры тяжести однородных куба, сферы, кольца, прямоугольной
или круглой пластины лежат в геометрическом центре этих тел.

Метод разбиения.

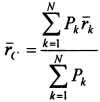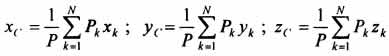Этот метод основан на применении формул и . Его используют, когда тело можно разбить на ряд частей, центры тяжести которых известны из условий симметрии. Метод разбиения можно наглядно проиллюстрировать с помощью рисунка.

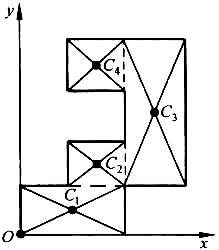
Расположив тело в системе координат, разделив его мысленно на отдельные части, веса которых Р1, Р2, Р3, Р4, а центры тяжести известны, вычислим вес тела и, согласно формулам 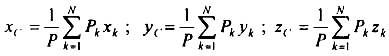, координаты центра тяжести С всего тела. Если тело имеет вырез, причем известны центр тяжести тела без выреза и центр тяжести вырезанного тела, то для определения координат центра тяжести используют метод отрицательных масс (частный случай метода разбиения).

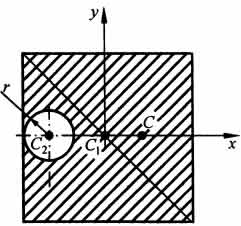
На рисунке изображена квадратная пластина, сторона которой а. В пластине выполнено круглое отверстие с радиусом r=0,2а и координатами центра x2=-0,3а; у2=0. Координаты центра тяжести С, пластины без отверстия x1=0, у1=0. Рассмотрим два тела: пластину без отверстия и диск, соответствующий вырезанному отверстию. При использовании формул 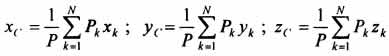вес диска будем считать отрицательным. Тогда 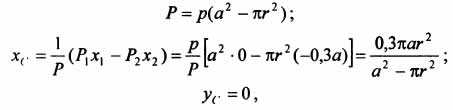, где р — вес единицы площади пластины.