Траектория, скорость и ускорение точки при задании движения на плоскости в полярных координатах.
Если движение точки происходит в некоторой плоскости, то иногда целесообразно использовать полярную систему координат. Положение точки М в ней определяется координатами r и "фи", являющимися скалярными величинами.
Расположение полярной оси (луча, проведенного на плоскости из некоторой точки О) выбирают в плоскости движения точки, исходя из удобства решения задачи.
Полярный радиус r - скалярный неотрицательный параметр, равный длине отрезка ОМ, т.е. расстоянию от начала координат (точки О) до точки М.
Полярный угол "фи" - это угол между полярной осью и илнией ОМ (за положительное значение значение угла принимают направление, противоположное направлению движения часовой стрелки).
Для задания движения точки в полярной системе коодинат необходимо иметь уравнение движения в виде: 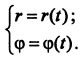 Данная система является также параметрической формой записи уравнения траектории точки. Если из системы исключить время, то уравнение траектории можно получить в форме:
Данная система является также параметрической формой записи уравнения траектории точки. Если из системы исключить время, то уравнение траектории можно получить в форме: 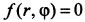 .
.
В полярной системе координат радиус-вектор точки, проведенный из центра О, равен 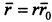 и выражается так:
и выражается так: 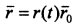 .
.
Вектор скоростипредставляется в виде суммы двух векторов, каждый из которых является составляющей скорости по направлению, задаваемому векторами r0 и p0 соответственно. Первое слагаемое называется радиальной составляющей, а второе - трансверсальной составляющей скорости точки: 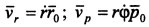 . Проекции скорости на радиальную и трансверсальную оси имею вид
. Проекции скорости на радиальную и трансверсальную оси имею вид 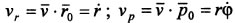 . Так как составляющие скорости взаимно перпендикулярны, то ее модуль:
. Так как составляющие скорости взаимно перпендикулярны, то ее модуль: 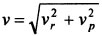 .
.
Ускорение точки: 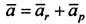 , где
, где 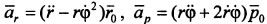 - радиальная и трансверсальная составляющие ускорения точки соответственно. Так как составляющие ускорения взаимно перпендикулярны, то его модуль:
- радиальная и трансверсальная составляющие ускорения точки соответственно. Так как составляющие ускорения взаимно перпендикулярны, то его модуль: 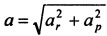 .
.
Дата добавления: 2018-11-26; просмотров: 1937;











