Траектория, скорость и ускорение точки при задании движения в декартовой системе координат.
Траектория, скорость и ускорение точки при векторном способе задания движения.
Положение точки в пространстве определяется радиус-вектором.
Уравнение движения в векторной форме: r=r(t)
Траектория точки - годограф ее радиус-вектора.
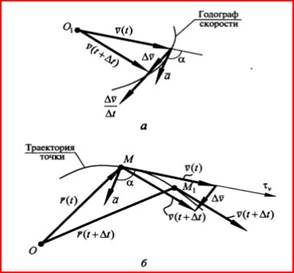
Скорость:
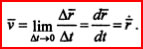
Ускорение:
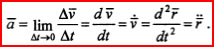
Траектория, скорость и ускорение точки при задании движения в декартовой системе координат.
Положение точки М в пространстве с использованием данной системы координат задается ее координатами x, y, z. 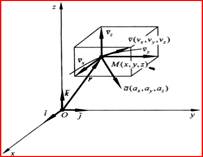
Чтобы знать положение точки в пространстве в любой момент времени необходимо иметь уравнения движения точки в виде: x=x(t), y=y(t), z=z(t).
x=x(t), y=y(t), z=z(t) - представляют собой уравнения движения точки в декартовой системе координат и одновременно являются уравнениями траектории точки, записанными в параметрической форме, где параметром является время t. Чтобы найти уравнение траектории в форме непосредственной зависимости между координатами x, y, z, из системы уравнений x=x(t), y=y(t), z=z(t) необходимо исключить время. В таком случае траекторию будет определять, например, система уравнений вида: f1(x,y)=0, f2(x,z)=0. Следовательно, траектория
представляет собой линию пересечения цилиндрических поверхностей, уравнения которых составляют систему f1(x,y)=0, f2(x,z)=0.
Скорость: 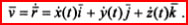
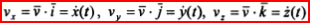 . Таким образом, скорость точки представляет собой сумму составляющих векторов, параллельных осям декартовой системы координат:
. Таким образом, скорость точки представляет собой сумму составляющих векторов, параллельных осям декартовой системы координат: 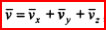 , где
, где 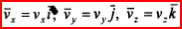 , а ее численное значение (модуль) определяется по формуле:
, а ее численное значение (модуль) определяется по формуле: 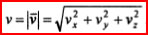 .
.
Ускорение: 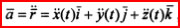 , проекции ускорения на оси декартовой системы координат будут
, проекции ускорения на оси декартовой системы координат будут 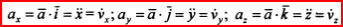 , составляющие ускорения, параллельные осям координат, определятся как
, составляющие ускорения, параллельные осям координат, определятся как 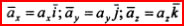 , а численное значение ускорения будет равно:
, а численное значение ускорения будет равно: 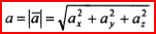 . Проекцию ускорения на ось, совпадающую по направлению с вектором скорости. для определения характера движения точки (т.е. ускоренно или замедленно она движется) можно в данном случае найти, в виде:
. Проекцию ускорения на ось, совпадающую по направлению с вектором скорости. для определения характера движения точки (т.е. ускоренно или замедленно она движется) можно в данном случае найти, в виде: 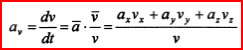 .
.
Дата добавления: 2018-11-26; просмотров: 2191;











