Касательные напряжения при изгибе

1 23

Как было установлено ранее, в поперечных сечениях балки при поперечном изгибе возникают не только нормальные, но и касательные напряжения, вызывающие деформации сдвига. В силу закона парности такие же касательные напряжения будут возникать и в продольных сечениях, параллельных нейтральному слою. Наличие касательных напряжений в продольных сечениях подтверждается появлением в деревянных балках при поперечном изгибе продольных трещин.

Перейдем к выводу формулы для определения касательных напряжений при поперечном изгибе балок прямоугольного сечения. Эта формула была выведена в 1855 г. русским инженером-мостостроителем Д.И.Журавским. Потребность в такой формуле была вызвана тем, что в XIX в. при строительстве мостов широко применялись деревянные конструкции, а балки из древесины обычно имеют прямоугольное сечение и плохо работают на скалывание вдоль волокон.

Af_H+dM,,

Эпюра М_и

Рис. 23.19

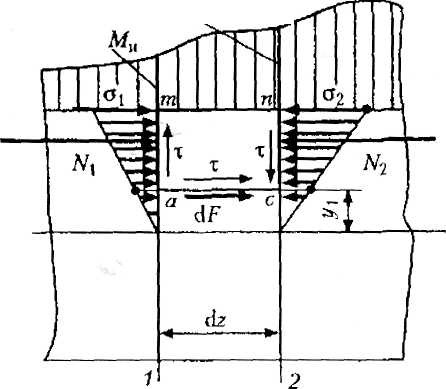
Рассмотрим балку прямоугольного сечения 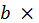h (рис. 23.19). Пусть в поперечном сечении 1действует изгибающий момент М_и, а в сечении 2, отстоящем от первого на бесконечно близком расстоянии dz, — изгибающий момент M_u+ dM_u. На расстоянии у_х от нейтральной оси проведем продольное сечение ас и рассмотрим равновесие элементарного параллелепипеда атпс, имеющего измерения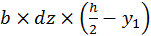

Равнодействующую нормальных внутренних сил, действующих на грань am, обозначим N₁ а действующих на грань cn — N₂; переменные нормальные напряжения в этих гранях обозначим соответственно δ_] и δ₂.

В поперечном сечении балки выделим бесконечно узкую полоску dA, находящуюся на переменном расстоянии у от нейтральной оси, тогда

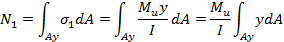
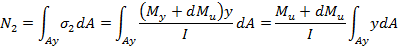
Предполагаем, что касательные напряжения в поперечном сечении прямоугольной балки параллельны поперечной силе Q и по ширине сечения распределены равномерно. Полагая, что в продольном сечении касательные напряжения α также распределены равномерно, определим касательную силу dF, действующую на грани ас.

dF= xbdz.

Составим уравнение равновесия параллелепипеда атпс:

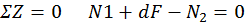
oткуда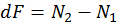

или ,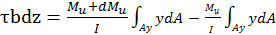

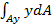обозначим через S, это статический момент заштрихованной площади А_у сечения относительно нейтральной оси; тогда

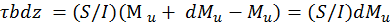
откуда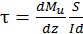

Так как согласно теореме Журавског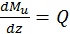о то ).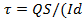

Это равенство называется формулой Журавского.

Выведенная формула дает значение касательных напряжений в продольных сечениях, но по закону парности в точках поперечного сечения, лежащих на линии пересечения продольной и поперечной плоскостей, будут действовать одинаковые но модулю касательные напряжения.

Формула Журавского читается так: касательные напряжения в поперечном сечении балки равны, произведению поперечной силы Q на статический момент S относительно нейтральной оси части сечения, лежащей выше рассматриваемого слоя волокон, деленному на момент инерции I всего сечения относительно нейтральной оси и на ширину b рассматриваемого слоя волокон.

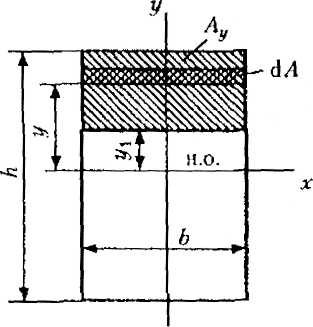
Определим закон распределения касательных напряжений для балки прямоугольного сечения (рис. 23.20). Для слоя волокон ad:

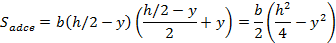
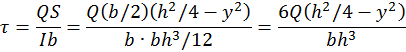
При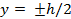

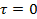
При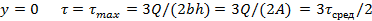

Таким образом, в верхнем и нижнем слоях волокон касательные напряжения равны нулю, а в волокнах нейтрального, слоя они достигают максимального значения. Законы распределения касательных напряжений по ширине и высоте прямоугольного сечения показаны

на рис. 23.20.

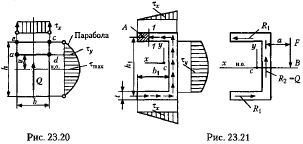
С некоторым приближением формулу Журавского можно применять для определения касательных напряжений в балках с поперечными сечениями другой формы. Рассмотрим консольную балку корытного профиля, сечение которой показано на рис. 23.21, изгибаемую силой F на конце.

Плоскостью 1-1 отсечем часть полки площадью А. Так как изгиб балки поперечный, то в плоскости 1—1 будут действовать продольные касательные силы и напряжения 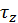(см. рис. 23.19). По закону парности в поперечном сечении полки возникнут касательные напряжения \_х той же величины, и их можно определить но формуле Журавского:

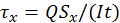
где Q — поперечная сила в сечении балки; S_x — статический момент отсеченной площади A относительно оси х (нейтральная ось),

S_x = Ah₁ /2; I — момент инерции всего сечения относительно нейтральной оси; t — толщина полки.

Если полка постоянной толщины, то касательные напряжения х_х изменяются по линейному закону, тогда

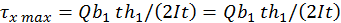
Равнодействующая R₁ касательных напряжений в верхней полке равна:

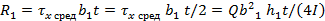
На нижнюю полку действует такая же сила R₁, но направленная в противоположную сторону. Две силы R₁ образуют пару с моментом

М_к=R₁h₁

Следовательно, в сечении наряду с вертикальной поперечной силой Q =R₂ возникает также крутящий момент М_к который скручивает балку; R₂ — равнодействующая касательных напряжений в стенке балки.

Чтобы деформации кручения не было, внешнюю силу F следует приложить в какой-то точке В на расстоянии а от середины стенки и соблюсти условие Fa = М_k откуда

a=M_k/F

Такая точка В называется центром изгиба. Если сечение балки имеет две oси симметрии, то центр изгиба совпадает с центром тяжести сечения.

Без вывода приведем формулу для определения максимальных касательных напряжений у балки круглого сечения:

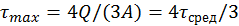
Касательные напряжения в балках соответствуют деформации сдвига, в результате чего плоские поперечные сечения при поперечном изгибе не остаются плоскими, как при чистом изгибе, а искривляются (рис. 23.22).

Большинство балок рассчитывают только по нормальным напряжениям; три вида балок следует проверять по касательным напряжениям, а именно: деревянные балки, так как древесина плохо работает на скалывание; узкие балки (например, двутавровые), так как максимальные касательные напряжения обратно пропорциональны ширине нейтрального слоя; короткие балки, так как при относительно небольших изгибающем моменте и нормальных напряжениях у таких балок могут возникать значительные поперечные силы и касательные напряжения.

Максимальное касательное напряжение в двутавровом сечении определяется по формуле Журавского. В таблицах сортамента приведены значения статического момента площади полусечения для двутавров и швеллеров.

Пример 23.7.Консольная балка, жестко защемленная одним концом в заделке, состоит из двух деревянных брусьев квадратного сечения, соединенных на другом конце болтом (рис. 23.23). К свободному концу балки приложена сила R=15 кН. Длина балки l = 2 м. Определить диаметр 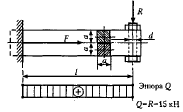стержня болта, если допускаемое напряжение среза 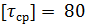МПа. Размер сечения брусьев а= 20 см.

Решение. Во всех поперечных сечениях балки кроме изгибающего момента возникает поперечная сила Q= R= 15 кН и соответствующие ей касательные напряжения сдвига, определяемые по формуле Журавского, причем максимальные напряжения 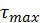возникают на нейтральной оси, т.е. в месте соприкосновения брусьев.

По закону парности такие же касательные напряжения возникают и в продольных сечениях балки. Тогда

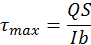
где 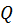— поперечная сила 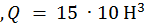; S — статический момент площади полусечения балки относительно нейтральной оси, 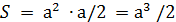; I — момент инерции всего сечения относительно нейтральной оси; I= а(2а)³/12= 2а⁴/3; b — ширина сечения, b = а.

Подставив эти выражения в формулу Журавского, получим:

X_max=3Q/(4a²)

Подставляя числовые значения и учитывая размерности, найдем

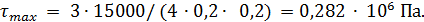
Сила сдвига F= X_max A_сд,где A_сд— площадь сдвига, А_сд=а1.

Вычислим F:

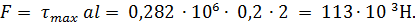
Сила F, действующая на стыке балок, стремится срезать болт. Найдем необходимый диаметр d стержня болта из расчета его на срез:

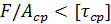
где А_ср — площадь среза, равная площади поперечного сечения стержня болта, A_ср = nd² /4.

Подставляя это выражение в расчетную формулу, получим

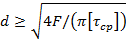
Подставим числовые значения:

1 23

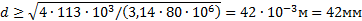
Дата добавления: 2020-06-09; просмотров: 444;

Поиск по сайту

Узнать еще