Расчеты на прочность при изгибе

Условие прочности балки при изгибе заключается в том, что максимальное нормальное напряжение в опасном сечении не должно превышать допускаемое.

Полагая, что гипотеза о не надавливании волокон справедлива не только при чистом, но и при поперечном изгибе, мы можем нор­мальные напряжения в поперечном сечении определять при попе­речном изгибе по той же формуле, что и при чистом изгибе. Вопрос о проверке прочности балки на каса­тельные напряжения, а также о рас­чете балок на жесткость будет рас­смотрен в последующих подразде­лах.

Расчетная формула на прочность при изгибе имеет вид

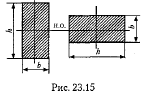
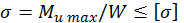
и читается так: нормальное напряжение в опасном сечении, опреде­ленное по формуле 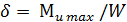, не должно превышать допускае­мое. Допускаемое нормальное напряжение при изгибе выбирают та­ким же, как и при растяжении и сжатии.

Максимальный изгибающий момент определяют из эпюр изги­бающих моментов или расчетом.

Так как момент сопротивления изгибу W в расчетной формуле стоит в знаменателе, то чем больше W, тем меньше будут расчет­ные напряжения.

Определим моменты сопротивления изгибу наиболее распро­страненных сечений:

1. Прямоугольник размером b x h (рис. 23.15):

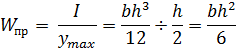
Если балку прямоугольного сечения положить плашмя, то 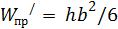, тогда

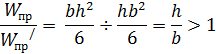
следовательно, при прочих равных условиях максимальные нор­мальные напряжения 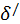у прямоугольной балки, положенной плаш­мя, будут больше, чем у той же балки, когда ее наибольший габарит­ный размер h вертикален (имеется в виду, что изгиб происходит в вертикальной плоскости).

Из этого следует правило: для обеспечения максимальной проч­ности ось, относительно которой момент инерции максимален, должна быть нейтральной.

1. Круг диаметром d: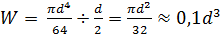

3. Кольцо размером :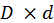

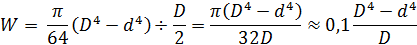
Момент сопротивления кольцевого сечения нельзя определять как разность моментов сопротивлений большого и малого кругов. Нетрудно подсчитать, что при одинаковой площади поперечного сечения, т.е. одинаковом расходе материала, момент сопротивле­ния кольцевого сечения больше момента сопротивления сплошно­го круглого сечения.

Так как вблизи нейтральной оси материал мало напряжен, то выгодно больше материала располагать дальше от нейтральной оси. Поэтому в машиностроении редко применяют металлические бал­ки прямоугольного сечения, но весьма широко распространены прокатные профильные балки таврового, двутаврового, углового, швеллерного и других сечений. Моменты инерции, моменты со­противления и другие характеристики прокатных фасонных про­филей стандартных размеров приведены в таблицах ГОСТа [7].

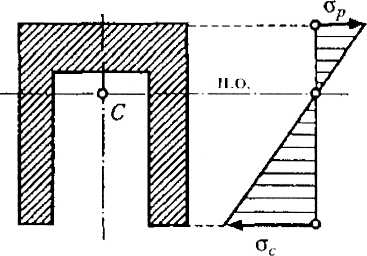
Для балок, материал которых неодинаково работает на растяже­ние и сжатие (например, чугун), целесообразно применять профи­ли, не симметричные относительно нейтральной оси, например тавровый или П-образный. Так как у несимметричного профиля при изгибе возникают неодинаковые напряжения растяжения и сжатия, то сечение, например, чугунной балки выгодно распола­гать так, чтобы меньшие напряжения были в зоне растянутых, а большие — в зоне сжатых волокон (рис. 23.16).

Проведем сравнение экономичности по массе балок двутаврово­го, прямоугольного и квадратного сечений.

Предположим, что из расчетного уравнения мы определим мо­мент сопротивления изгибу балки:

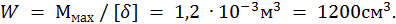
По таблицам ГОСТа выбираем двутавровый профиль № 45 с

площадью поперечного сечения

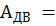
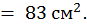
Определим размеры прямоуголь­ного сечения, полагая h=2b

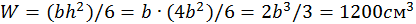
откуда 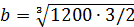=12,2см; ;

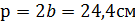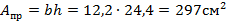
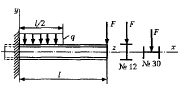
Рис. 23.16

При прочих равных условиях массы балок пропорцио­нальны площадям поперечных сечений:

.

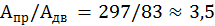Балка прямоугольного сечения о три с половиной раза тяжелее балки двутаврового профиля при одинаковой прочности и прочих равных условиях.

Определим размеры квадратного сечения со стороной a:

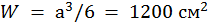, откуда ;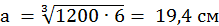

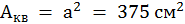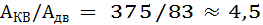
Балка квадратного сечения е четыре с половиной раза тяжелее балки двутаврового профиля при одинаковой прочности и прочих равных условиях.

Пример 23.5.Определить номер профиля консольной балки двутав­рового сечения, если допускаемое напряжение при изгибе [δ]=120 МПа, F=2000 Н, q = 4000 Н/м, l = 2 м (рис. 23.17).

Р е ш е н и е. Очевидно, что у данной балки, работающей на изгиб, максимальный изгибающий момент будет в заделке и определится но формуле

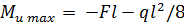
Подставив данные, получим абсолютное значение момента

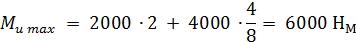
Расчетное уравнение на прочность при изгибе имеет вид:

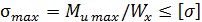
откуда

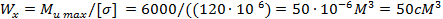
Найдя по таблицам сортамента ближайшее большее значение для W_x, выбираем двутавровое сечение № 12, для которого W_x= 58,4 см². Если се­чение балки повернуть на 90°, т.е. расположить полки вертикально, а стенку — горизонтально (см. рис. 23.17), то потребуется профиль №30 (при таком расположении сечения двутавр подбирается по W_y). В этом случае балка окажется в три раза тяжелее.

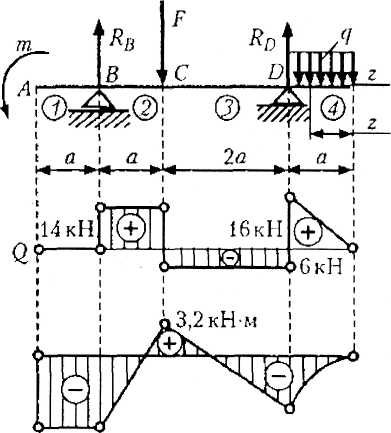
Пример 23.6.Построить эпю­ры поперечных сил и изгибающих моментов для балки, изображен­ной на рис. 23.18, если F = 20 кН, q = 20 кН/м , 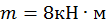, а=0,8м. Проверить балку на прочность, если ее профиль — двутавр № 20, а допускаемое напряжение [δ] = 150 МПа.

Решение. Определим опор­ные реакци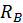и и 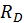, составив уравнение моментов относитель­но точек B и D:

Рис. 23.18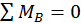

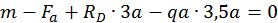
Подставив данные и произведя вычисления, получим ;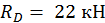

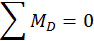
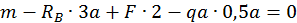
Подставив данные и произведя вычисления, получим R_B =14 кН.

Построим эпюру Q .На первом участке Q₁= 0, так как алгебраическая сумма сил пары всегда равна нулю.

На втором участке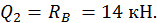

На третьем участке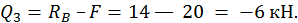

На этих участках эпюра Q изображается прямыми линиями, парал­лельными оси.

Четвертый участок рассмотрим, взяв начало координат на правом кон­це балки:

Q_A = qz, где z изменяется от 0 до а:

При z=0 Q₄=0

При z=a 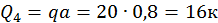Н

Эпюра изображается прямой наклонной линией.

В точке D эпюра Q имеет скачок, равный опорной реакции R_D.

Построим эпюру М_и На первом участке

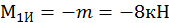
На втором и третьем участках строим эпюру по значениям изгибающего момента на границах участков:

в сечении В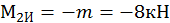

в сечении С ;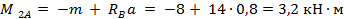

в сечении D

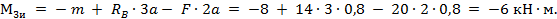
На первых трех участках эпюра М_и изображается прямыми линиями. Для построения эпюры М_ина четвертом участке начало координат возьмем на правом конце балки, тогда

М_4и = - qz²/2, где z изменяется от 0 до а:

При z=0 М_4и = 0;

При z =а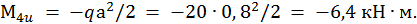

На четвертом участке эпюра М_и — дуга параболы. Проверим балку на прочность. Наибольший изгибающий момент бу­дет на первом участке: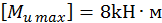

Расчетная формула на прочность при изгибе:

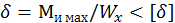
По таблицам сортамента находим значение момента сопротивления для двутавра № 20:

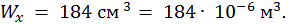
Подставляя значения и учитывая размерности, получим

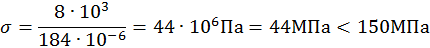
Условие прочности 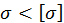выполнено. В данном случае балка работает с большой недогрузкой, следовательно, балку можно изготовить из двутавра меньшего размера, например № 14.