Математическая модель операции сборки

Операция сборки представляет собой элементарный акт технологического процесса над совокупностью элементов ЛА (ведущим и ведомыми элементами), в результате которого изменяется значение хотя бы одного из параметров ведущего элемента ЛА (за счет присоединения к нему ведомых), а соответствующие ведомые элементы прекращают существование. Соответствующий набор технологического оборудования, обеспечивающий выполнение операции сборки, называется сборочным агрегатом.

Сущность формализованной операции сборки состоит в переработке информации, описывающей состояния элементов ЛА, которые участвуют в сборке.

Для многих технологических процессов подготовки ЛА выбор одного из элементов ведущим (сборный узел) оказывается условным, особенно для первых сборочных операций, свойственных начальному периоду сборки аппарата.

Если в сборке участвуют сборный узел (ведущий элемент) и m деталей (ведомых элементов), параметры которых к моменту начала сборки t^H известны 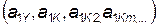, то в результате операции сборки мы получим новый узел с новыми значениями параметров а_2KY, а детали прекратят существование. Математически операция сборки описывается соотношениями вида

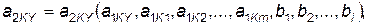(4.6)

где b_i — параметры, зависящие от характеристик сборочного агрегата. Определение моментов прекращения существования ведомых элементов проводится лишь в случае необходимости или принимается равным t^H или t^к.

Если а_2KY могут принимать случайные значения, то по аналогии с (10.3) имеем

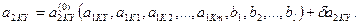(4.7)

При нахождении параметров, определяющих синхронизацию элементов операции сборки, могут быть использованы следующие соображения. Если 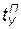— момент поступления на сборку узла, а 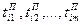— моменты поступления деталей и операция начинается в момент готовности всей совокупности элементов, то по аналогии с (4.4) можно записать

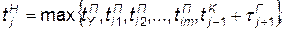. (4.8)

Если отдельные сборочные работы (части операции сборки) начинаются по мере поступления на сборку тех или иных элементов ЛА или по мере готовности определенных агрегатов сборки, то целесообразно рассматриваемую операцию сборки расчленить на несколько последовательно выполняемых операций.

Другим существенным параметром, определяющим режимы взаимодействия отдельных элементов оборудования во времени, является продолжительность операции сборки. При формализации операцию сборки удобно представить в виде последовательности этапов, которые условно можно назвать установкой элемента на узле; креплением элементов; регулировкой узла. В соответствии с этим и длительность операции рассматривается как сумма трех слагаемых, которые в общем случае являются случайными с заданными вероятностными характеристиками.

Следует отметить, что обычно при описании операции сборки определяются параметры только сборного узла, а параметры ведомых элементов не фиксируются. Это в значительной мере упрощает соотношения вида (4.6) и (4.7).

Составим модель функционирования операции сборки. Пусть операцией сборки предусматривается присоединение к подготавливаемому ЛА (ведущему элементу) нескольких ведомых элементов. Если в необходимый момент времени соответствующий ведомый элемент подан на сборку, то операция сборки происходит, в противном случае сборка срывается. Если ведомый элемент оказывается негодным, он заменяется другим. Операция сборки продолжается (t^СБ) ограниченное время 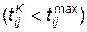. После окончания сборки и получения готового изделия или срыва операции сборки переходим к сборке последующего ЛA (t^п < Т). Вероятность Р^НГ того, что ведомый элемент может оказаться негодным известна, известно также время t^пр, затрачиваемое на проверку этого элемента.

Для построения моделирующего алгоритма операции сборки введем следующие операторы:

Ф₁ — формирование момента поступления ведущего элемента на сборку;

Р₂ — проверка условия t_j^П < Т;

Р₃ — проверка условия I > l_пр, где i — номер ведомого элемента, а l_пр — количество присоединяемых элементов;

Ф₄ — формирование параметров ЛА после сборки ;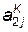

К₅ — счетчик количества готовых ЛА, реализующий операцию N+1;

К₆ — счетчик номеров ведущих элементов, реализующий операцию j+1;

F₇ — формирование i = 1;

F₈ — переход к новому ведущему элементу;

F₉ — подготовка к i-й сборочной операции;

Р₁₀ — проверка условий n_i > 0, где n_i — количество ведомых элементов номер i, имеющихся в ведущем элементе;

К₁₁ — счетчик количества срывов операции сборки;

К₁₂ — счетчик количества элементов номер i, реализующий операцию n_i- 1;

Ф₁₃ — формирование значения t^np;

Р₁₄ — проверка условия ξ < Р^НГ, где ξ — случайное число с равномерным распределением в интервале [0, 1];

Ф₁₅ — формирование длительности операции t^СБ;

А₁₆ — определение момента 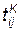окончания i-й операции с учетом потери времени t^пр;

Р₁₇ — проверка условия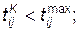

К₁₈ — счетчик номеров сборочных операций, реализующий операцию I +1;

F₁₉ — формирование I = i+1, т. е. имитация конца сборки;

К₂₀ — счетчик количества готовых ЛА, реализующий операцию N-1;

A₂₁ — обработка результатов моделирования;

Я₂₂ — выдача результатов.

Блок-схема моделирующего алгоритма операции сборки представлена на рис. 4.3.

Операторная схема моделирующего алгоритма для составной операции сборки

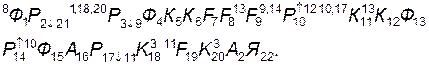
Сущность работы алгоритма.

Оператор Ф₁ формирует момент поступления на сборку j-го ведущего элемента t_j^П. Величина t_j^П сравнивается с Т (оператор Р₂), где Т— предельное время операции сборки < какое-то контрольное время). Если t_j^П < T, то моделирование продолжается, в противном случае управление передается оператору А₂₁ для обработки результатов моделирования.

Оператор Р₃ проверяет условие I > l, если I > l, то это значит что сборка данного элемента ЛА закончена и осуществляется переход к новому сборному узлу j+1 (оператор F₈) с попутным формированием 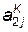(оператор Ф₄), подсчетом количества готовых ЛА (оператор К₅), определением номера нового сборного узла (оператор К₆) и формированием i = 1 (оператор F₇).

Если же условие, проверяемое оператором Р₃ не выполнено, то сборка элемента ЛА не закончена и осуществляется переход к оператору F₉ для подготовки к очередной сборочной операции.

Оператор Р₁₀ поверяет, имеются ли n_i > 0 детали, необходимые для сборки. Если деталей нет, то происходит срыв сборки (как i-й сборочной операции, так и составной операции) и управление передается оператору К₁₁ для подсчета количества срывов, а затем оператору F₁₉, который формирует I = l+1, т. е. имитирует конец сборки, а оператор К₂₀ вычитает единицу из количества готовых элементов ЛА для компенсации действия оператора К₅. Управление передается оператору Р₃. Теперь I >l, поэтому работа алгоритма будет продолжаться по знакомой нам цепи Р₃Ф₄...F₈Ф₁.

Если условие n_i > 0 выполняется (оператор Р₁₀), т. е. детали для сборки есть, то управление передается оператору K₁₂, который вычитает единицу из n_i (деталь взята для проверки), Ф₁₃ формирует длительность проверки t^np. Затем по жребию (оператор P₁₄) определяется качество детали. Если деталь негодна, то возвращаемся к P₁₀ и выбираем новую деталь, а если деталь годна, то продолжаем сборку: оператор Ф₁₅ формирует длительность, а A₁₆ определяет момент окончания i–й операции сборки 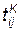. Если 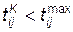(оператор Р₁₇), то переходим к К₁₈ (i+1), а затем к Р₃. Если это условие не выполнено, то получается срыв сборки (оператор К₁₁).

На практике встречаются и другие, более сложные модификации операции сборки. Их моделирование требует соответствующего изменения моделирующего алгоритма. Так, в рассмотренном примере предусматривалось, что отсутствие детали (n_i = 0) приводит к срыву сборки. Часто более приемлемым оказывается предположение, что при отсутствии детали сборный узел ожидает ее появления какое-то время и уже в противном случае происходит срыв сборки.