Квазистатический режим биполярного транзистора в усилительном каскаде

Графоаналитическое рассмотрение при большом сигнале

Упрощенная схема усилительного каскада на ВТ, включенного по схеме с об­щим эмиттером, показана на рис. 5.18. В этом каскаде используется один источ­ник питания E_К, а для задания постоянного напряжения U_ВХ применен делитель R₁, R₂. Резисторы R₁, R₂ выбирают такими, чтобы ток I = E_К/( R₁ + R₂) был много больше входного тока базы при отсутст­вии сигнала (I>>I_Б). Это позволяет иск­лючить влияние возможного изменения режима работы БТ на напряжение U_БЭ. Если задан ток I_Б, то U_БЭ находится по входной характеристика БТ. Теперь воз­никает вопрос, как определить соответст­вующую точку в семействе выходных ха­рактеристик, т.е. найти постоянное на­пряжение U_КЭ и постоянный ток I_К яри на­личии резистора R_К, и отсутствии сигнала (режим покоя, точка покоя)? По закону Кирхгофа

U_КЭ = E_К – I_К R_К (5.57)

Но ток I_К и U_КЭ должны соответствовать той статической характеристике, на которой отмечено в качестве параметра заданное значение I_Б:

I_К = f(U_КЭ), I_Б = const (5.58)

Из (5.57)

I_К = (E_К – U_КЭ)/ R_К (5.59)

Связь I_К и U_КЭ изображается прямой линией, называемой нагрузочной прямой, которая отсекает в системе координат I_К, U_КЭ отрезки на оси токов при U_КЭ = 0 I^*_К = E_К/R_К, а на оси напряжений при I_К = 0 U^*_КЭ = E_К,. Величины I^*_К и E_К, отмечены точками А иВ нагрузочной прямой на рис. 5.19. Чем больше нагрузочное сопротивление R_К, тем меньше I^*_К и меньше наклон нагрузочной прямой: при R_К → 0 она вертикальна, при R_К → ∞ приближается к оси абсцисс.

Нагрузочная прямая пересекает статические характеристики. Точки пере­сечения и определяют значения I_К и U_КЭ, которые соответствуют различным величинам тока базы I_Б (параметра этих характеристик). Точка С пересечения прямой с характеристикой, соответствующей заданному значению I_Б называ­ют точкой покоя.

Пусть на входе имеется низкочастотное синусоидальное напряжение сигнала с амплитудой U_{ВХ m}. Тогда напряжение между базой (входом) и общей точкой

U_ВХ (t)= U_БЭ + U_{ВХ m} sinωt (5.60)

Так как входные характеристики БТ в нормальном активном режиме слабо зависят от напряжения U_КЭ, то можно считать, что рабочая точка, определяющая ток в любой момент времени, перемещается по одной входной характеристике вверх и вниз в определенных пределах. При этом периодическое изменение базового тока приближенно можно представить выражением

I_Б (t)= I_Б + I_{Б m} sinωt (5.61)

где I_Бт – амплитуда переменной составляющей базового тока. При таком законе изменения базового тока соответствующая рабочая точка в семействе выходных характеристик будет перемещаться с частотой ω по нагрузочной прямой между точкой F, соответствующей максимальному значению тока базы U_Бmax= I_Б + I_Бт, и точкой, определяемой минимальным током U_Бmin= I_Б – I_Бт. При этом коллекторный ток изменяется от значения I_{К max} = I_К + I_{К m} до I_{К min} = I_К – I_{К m}, где I_{К m} – амплитуда переменной составляющей коллекторного тока. Предполагается, что изменение I_К также имеет синусоидаль­ный характер. Из-за наличия R_К изменение I_К вызывает синусоидальное изменение U_КЭ от значения U_{КЭ min} = U_КЭ – U_{ВЫХ т} до U_{КЭ max} = U_КЭ + U_{ВЫХ т}, где U_ВЫХт=I_КmR_К – амплитудное значение полезного сигнала на резисторе R_К, характеризующее усилитель­ный эффект биполярного транзистора.

Мы провели наглядное графоаналитическое рассмотрение усилительного каскада, которое стало возможным потому, что был принят большой сигнал на входе, когда все амплитуды токов и напряжений оказались значительными. Если входной сигнал настолько мал, что также малы изменения токов и напряжений, то графические построения теряют смысл (невозможны). Выход состоит в том, что введенные параметры (кроме расходуемых мощностей и КПД) можно рассчи­тать с помощью эквивалентных схем, основанных на использовании дифферен­циальных параметров (см. § 5.5.2).

Биполярный транзистор в квазистатическом режиме как линейный четырехполюсник

Дифференциальные параметры, введенные нами для стати­ческого режима (см. § 5.4), можно применять и для квазистатичес­кого режима, справедливого для низких частот сигнала, когда свя­зи между величинами остаются почти такими, как в статическом режиме (см. § 1.2).

Для этого достаточно в уравнениях (5.51) приращения (диффе­ренциалы) заменить малыми амплитудными значениями перемен­ных величин:

dI_ВХ = I_ВХm, dI_ВЫХ = I_ВЫХm, dU_ВХ = U_ВХm, dU_ВЫХ = U_ВЫХm

так,чтобы для системы h-параметров вместо (5.51) можнобыло на­писать

U_{ВХ m}= h₁₁I_ВХm + h₁₂U_ВЫХm (5.73)

I_ВЫХm = h₂₁I_ВХm + h₂₂U_ВЫХm

Приведеннаясистема уравнений как раз и совпадает с системой уравнений линейного четырехполюсника при использовании h-параметров, которые являются постоянными коэффициентами. Повторяем, что такая замена приращений величин статического режима переменными составляющими справедлива только для квазистатического режима. Поэтому h-параметры в системе (5.73) можно нахо­дить по статическим характеристикам.

Для нахождения параметров h₁₁ и h₂₁ в теории четырехполюс­ников необходимо на низких частотах сделать опыт короткого за­мыкания на выходе по переменному напряжению (U_ВЫХm = 0). От­сутствие переменного напряжения при использовании статичес­ких характеристик означает постоянство выходного напряжения (U_ВЫХ = const). Для нахождения в теории четырехполюсника пара­метров h₁₂ и h₂₂ проводится опыт холостого хода по переменному току на входе. Но при имитации этого опыта на статических характе­ристиках это эквивалентно постоянству входного тока (I_ВХ = const). Это отмечалось в § 5.3.

Уравнения, аналогичные (5.73), применяют и для описания це­пей, когда нельзя пренебречь влиянием реактивных элементов, например, емкостных составляющих токов, так как связи при малом сигнале и в этом случае остаются линейными, как у четырехполюс­ника. Необходимо только ввести комплексные амплитуды, h-параметры должны стать комплексными (частотозависимыми):

(5.74)

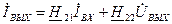
Конечно, комплексные параметры уже нельзя определить по стати­ческим характеристикам и требуются специальные измерения.

В справочниках по транзисторам обычно приводятся значения h-параметров для низких частот, когда эти величины являются дей­ствительными. На высоких частотах из-за влияний паразитных ем­костей трудно экспериментально осуществить режим холостого хо­да во входной цепи по переменной составляющей. Поэтому на высо­ких частотах более удобна система y-параметров, в которой легко реализуются режимы короткого замыкания по переменному току без нарушения режима работы транзистора по постоянному току: необ­ходимо шунтировать входную и выходную цепи конденсатором дос­таточно большой емкости.

Уравнения при использовании у-параметров для высоких частот имеют вид

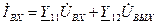(5.75)

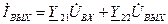
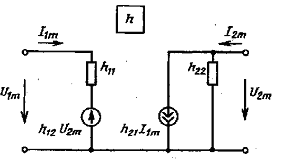
рис. 5.20

В теории простейших четырехполюсников широко используют­ся эквивалентные схемы на основе систем h-, у-, z-параметров. Их можно применять для биполярных транзисторов (рис. 5.20). Значе­ния параметров действительные. Недостаток эквивалентныхсхемзаключается в том, что значения параметров одного транзистора изменяются при замене схемы включения БТ. Так как дифферен­циальные параметры сложным образом связаны с физическими процессами БТ и, кроме того, зависят от схемы включения БТ, то эквивалентные схемы БТ часто называют формальными или эквивалентными схемами с внешними параметрами четырехполюсни­ка.

5.6. Нелинейная и линейная динамические модели
биполярного транзистора

5.6.1. Нелинейная динамическая модель биполярного транзистора

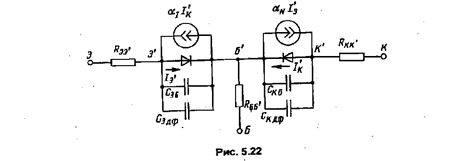
Наиболее распространенной нелинейной моделью БТ для ди­намического режима является модель, основанная на статической модели Эберса-Молла. Инерционные свойства БТ учитываются путем включения емкости эмиттерного перехода С_Э и коллекторно­го перехода С_К (рис. 5.22). Каждая из этих емкостей складывается из барьерной и диффузионной емкостей переходов:

С_Э= С_{Э б} + С_{Э дф}; С_К= С_{К б} + С_{К дф}

где С_{Э б}, С_{К б} – барьерные емкости переходов, учитывающие токи смещения, а С_{Э дф}, С_{К дф} – диффузионные емкости в областях вне границ переходов.

Параллельное соединение безынерционного диода, предста­вляющего собой ВАХ эмиттерного перехода, и емкости С_Э – это нелинейная электрическая модель «изолированного» эмиттерно­го перехода. Добавление к этой модели зависимого генератора тока α_II'_К, учитывающего собирающее действие эмиттерного пе­рехода для носителей, инжектированных коллектором, превра­щает эту часть схемы в нелинейную электрическую модель реаль­ного эмиттерного перехода в транзисторе. То же можно сказать и о коллекторном переходе.

Полученная схема соответствует прямому включению обоих пе­реходов в статическом режиме, т.е. режиму насыщения или двухсто­ронней инжекции. Заметим, что при таком изображении нелинейной модели коэффициенты передачи в зависимых генераторах нор­мального активного режима α_N инверсного активного режима α_I соответствуют статическому режиму работы БТ, т.е. являются параме­трами» не зависящими от частоты сигнала.

Значения барьерной и диффузионной компонентов емкостей С_Э и С_К зависят от напряжения на переходах, что усложняет про­цесс анализа и расчеты в динамическом режиме, когда эти вели­чины изменяются. Кроме того, необходимо учитывать, что емко­сти не изменяются мгновенно с изменениями напряжения, а обла­дают собственной инерционностью. Объясняется это тем, что формирование емкостей (изменение зарядов) связано с движени­ем носителей заряда и такими понятиями, как время жизни, время пролета, время максвелловской релаксации.

Обратим внимание еще на одно принципиальное отличие ди­намической модели от статической модели Эберса-Молла. Ста­тическая модель является универсальной в том смысле, что она без изменений применима для всех схем включения БТ и всех ре­жимов работы (нормального активного, инверсного активного, от­сечки и насыщения). Используя уравнения этой модели, можно определить все токи и статические характеристики, предвари­тельно вычислив напряжения на переходах. Практически при ис­следовании какого-либо режима схема может существенно упро­щаться, так как удобнее выражать токи зависимых генераторов в каждой схеме со своим управляющим воздействием и своим ко­эффициентом передачи тока.

Рассмотрим схемы включения БТ с общей базой и общим эмит­тером. Входной сигнал в динамическом режиме подается между об­щим и входным электродами. Входным электродом будут эмиттер в схеме с ОБ и база в схеме с ОЭ. Цепь, в которую входят общий и входной электроды, называют входной. Цепь, содержащую общий электрод и коллектор, называют выходной, а сам коллектор – выход­ным электродом. В коллекторную (выходную) цепь включают нагруз­ку, на которой создается выходной сигнал или отклик на управляю­щее воздействие во входной цепи.

Внешнее отличие динамической модели БТ от статической состоит в наличии в первой реактивных элементов (емкостей С_Э и С_К). Очевидно, что отклик в выходной цепи (или переход­ный процесс) будет зависеть от того, между какими элемента­ми или точками модели включается входной сигнал (генератор сигнала), так как реактивные параметры модели будут влиять по-разному.

5.6.2. Линейная (малосигнальная) модель биполярного транзистора

В качестве малосигнальных моделей могут быть использованы эквивалентные схемы с дифференциальными h-, у- и z-параметрами, рассмотренные в § 5.5. Там же отмечался формальный харак­тер этих схем, зависимость дифференциальных параметров от схемы включения транзистора и отсутствие непосредственной свя­зи с физической структурой транзистора. Поэтому нашли широкое распространение эквивалентные схемы с так называемыми физи­ческими параметрами, которые опираются на нелинейную динамическую модель Эберса-Молла, т.е. тесно связаны с физичес­кой структурой биполярного транзистора.

Малосигнальную схему БТ легко получить из нелинейной ди­намической модели заменой эмиттерного и коллекторного диодов их дифференциальными сопротивлениями, устанавливающими связь между малыми приращениями напряжения и тока. Кроме то­го, в усилительных схемах используется либо нормальный актив­ный, либо инверсный активный режим, а режим насыщения недо­пустим. Поэтому при переходе к малосигнальной схеме можно ог­раничиться рассмотрением наиболее распространенного нор­мального активного режима, так как результаты легко перенести и на инверсный активный режим. В этом случае можно исключить генератор тока и малосигнальную модель БТ для схемы включе­ния с ОБ изобразить, как на рис. 5.23.

Поясним смысл элементов модели. Резистор r_Э представляет дифференциальное сопротивление эмиттерного перехода. В пер­вом приближении его можно определить по формуле для идеализи­рованного р-n-перехода:

r_Э = dU/dI ≈ φ_T/I_Э (5.76)

где I_Э – постоянная составляющая тока эмиттера. Так как при комнатной температуре φ_T =0,026 В, то при I_Э = 1 мА r_Э = 26 Ом.

Величина r_К называется дифференциальным сопротивлением коллекторного перехода. Оно обусловлено эффектом Эрли и мо­жет быть определено по наклону выходной характеристики:

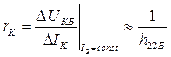(5.77)

Величина r_К обратно пропорциональна значению h_22Б – парамет­ра (5.43), называемого выходной проводимостью БТ. Дифференциальное сопротивление коллектора может составлять сотни килоом и мегаомы, тем не менее его следует учитывать.

Реактивные элементы модели (С_Э, С_К) оказались теперь присое­диненными параллельно резисторам r_Э и I_К. Сопротивления облас­тей Rээ', R_KK' и R_ББ' в схеме оставлены, хотя обычно из нее исключа­ют малое сопротивление Rээ' (Rээ' << r_Э) и иногда R_KK' (десятки ом). Сопротивление базы R_ББ', которое может превышать сотни ом, все­гда остается в модели.

Следует заметить, что коэффициент передачи в малосигналь­ной модели должен быть дифференциальным, т.е. определяться через приращения:

(5.78)

а не через отношение токов, как это было ранее в нелинейной модели:

(5.79)

Этот коэффициент называют интегральным коэффициентом пе­редачи тока. Значения α_{N инт} и α_{N диф} обычно мало отличаются, поэ­тому дополнительные индексы «диф» и «инт» можно опустить, пока в этом нет специальной необходимости.

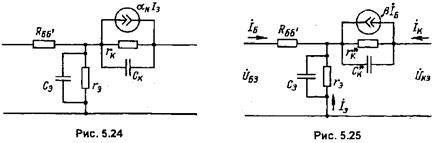
Приведенная эквивалентная малосигнальная модель БТ формально относится к схеме включения с ОБ. Однако она при­менима и для схемы с ОЭ. Для этого достаточно поменять мес­тами плечи этой схемы, называемой Т-образной схемой с фи­зическими параметрами. Электрод «Б» следует изобразить входным, а «Э» – общим, как показано на рис. 5.24. Значения всех элементов остаются прежними. Однако при таком изобра­жении появляется некоторое неудобство, связанное с тем, что зависимый генератор тока в коллекторной цепи выражается не через входной ток (ток базы). Этот недостаток легко устранить преобразованием схемы к виду, изображенному на рис. 5.25. Чтобы обе схемы были равноценными четырехполюсниками, они должны иметь одинаковые параметры в режимах холо­стого хода и короткого замыкания. Это требует перехода от тока α_N 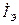к току β и замены r_К и С_К на r^*_К и С^*_К соответственно. Связи этих величин определяются формулами

r^*_К =α r_К / β = r_К /( β+1) (5.80)

С^*_К =( β+1) С_К (5.81)

Легко убедиться, что r^*_К характеризует наклон выходной характери­стики (эффект Эрли) в схеме с ОЭ и связан с выходной проводимо­стью в этой схеме соотношением (5.43). Во сколько раз уменьшает­ся r^*_К по сравнению с r_К, во столько же раз возрастает емкость С^*_К по сравнению с С_К, т.е. r_К С_К = r^*_К С^*_К.

ТИРИСТОРЫ