КОНЕЧНЫЕ АВТОМАТЫ С ПАМЯТЬЮ (АСИНХРОННЫЕ ПОСЛЕДОВАТЕЛЬНОСТНЫЕ СХЕМЫ)

В отличие от комбинационных логических схем, выходные сигналы автоматов зависят от состояния на входах и предыдущего внутреннего состояния схемы, то есть автомат обладает памятью (автомат с памятью – АП). В каждый момент времени схема находится в каком-либо состоянии из конечного их числа (поэтому такие автоматы называются конечными). Это состояние определяется совокупностью значений внутренних переменных (или совокупностью состояний всех элементов памяти). Комбинация внутреннего состояния и состояния выхода называется полным состоянием. В зависимости от внутреннего состояния АП различным образом реагирует на один и тот же набор входных сигналов (вектор 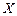). Воспринимая входные сигналы при определённом состоянии, АП переходит в новое состояние и вырабатывает новые значения выходных переменных (вектор 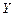), то есть выход АП и его следующее внутреннее состояние являются функциями текущего полного состояния.

Поведение АП можно описать следующей системой логических функций:

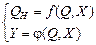
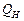и – состояния АП до и после подачи входных сигналов (индекс «Н» – от слова «новое»).

Когда следующее внутреннее состояние то же, что и текущее внутреннее состояние, то полное состояние считается устойчивым в том смысле, что невозможно появление никаких изменений до тех пор, пока не изменится состояние входа.

Формальной математической моделью последовательностных схем является абстрактный конечный автомат, определяемый конечными множествами состояний входов 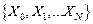, состояний выходов 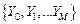, внутренних состояний 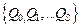, а также функциями переходов 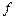и выходов 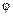, определяющих последовательность смены внутренних состояний и состояний выходов автомата в зависимости от смены состояний входов. Кроме того, из множества внутренних состояний обязательно выделяется некоторое состояние 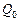, называемое начальным внутренним состоянием.

Переходы АП из одного состояния в другое начинаются с некоторого начального состояния 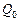, задание которого является частью описания автомата. Следующее состояние зависит от 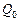и поступивших входных сигналов 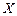. В конечном счёте, текущее состояние и выходные сигналы автомата зависят от начального состояния и всех векторов 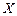, поступивших на автомат в предшествующие моменты времени. Таким образом, последовательность входных сигналов определяет последовательность смены внутренних состояний и выходных сигналов, поэтому такие схемы часто называют последовательностными.

Структурно АП отличаются от комбинационных схем наличием обратных связей, что приводит к появлению свойств запоминания состояний. В каноническом представлении АП разделяются на две части: комбинированную логическую схему (КЛС) и память (рис. 1). На входы КЛС подаются входные сигналы 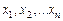и сигналы состояния АП 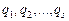, а на её выходах вырабатываются выходные сигналы 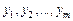и сигналы для перевода АП в новое состояние .

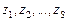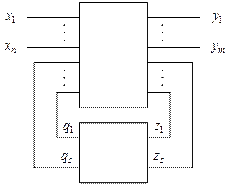
Рис. 1

Предполагается, что автомат функционирует в дискретные моменты времени, то есть непрерывная шкала времени разделена на интервалы, пронумерованные целыми положительными числами 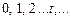Эти интервалы называются тактами. На протяжении одного такта сохраняются неизменными состояния входа, выхода и внутреннее состояние автомата. В зависимости от того, чем определяется длительность тактов ( ), различают два класса автоматов: синхронные и асинхронные (рис. 2).

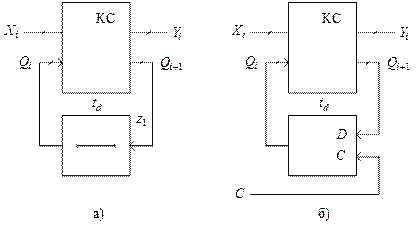
Рис. 2. Асинхронный (а) и синхронный (б) АП

Синхронные автоматы характеризуются тем, что имеются тактовые (или синхронизирующие) сигналы , которые разрешают элементам памяти приём данных только в определённые моменты времени. Элементами памяти в данном случае служат синхронные триггеры. Процесс обработки информации упорядочивается во времени и в течение одного такта происходит переход к следующему внутреннему состоянию. Частота тактового генератора выбирается такой, чтобы до появления следующего тактового импульса автомат успел перейти в новое внутреннее состояние.

В синхронных автоматах каждое внутреннее состояние устойчиво и переходные временные состояния не возникают. Борьба с последствиями рисков и гонок обеспечивается тем, что приём информации в элементы памяти разрешается только после завершения в схеме переходных процессов, что обеспечивается параметрами импульсов синхронизации. Для определения этих параметров необходимо просуммировать максимально допустимые задержки элементов самой длинной цепочки и выбрать интервал между двумя синхроимпульсами не меньше получившейся величины. При этом реальные переходные процессы в схеме будут, как правило, завершаться значительно раньше и быстродействие схемы будет недоиспользовано. Увеличение быстродействия схемы в таком случае сопряжено с риском потери работоспособности или увеличения вероятности сбоев в процессе эксплуатации.

В асинхронных автоматах длительность интервала времени 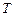, в течение которого остаётся неизменным состояние автомата является величиной переменной и определяется только моментами изменения состояния входных сигналов. Поэтому любой по продолжительности интервал времени, в течение которого сохраняется неизменным состояние входа, будет восприниматься автоматом как один и тот же интервал времени (один такт).

Характерным свойством асинхронного автомата является то, что при переходе из одного устойчивого состояния в другое, он обычно проходит через промежуточные нестабильные состояния, которые возникают из-за неодновременного срабатывания элементов памяти даже при одновременной подаче на них входных управляющих сигналов.

Поэтому для обеспечения предсказуемого поведения асинхронного АП применяются специальные методы кодирования внутренних состояний, обеспечивающие заданный алгоритм переходов.

В сравнении с асинхронными, синхронные АП значительно проще в проектировании, однако практическое применение такого класса устройств оправдано, если состояния автомата должны изменяться через равные промежутки времени, задаваемые параметрами тактового генератора.

В дискретных системах управления, предназначенных для формирования воздействий на управляемый объект и принимающих сигналы обратной связи от различных датчиков, характеризующих выполнение определённого действия или наступление некоторого события, продолжительность тактов может сильно различаться. В таком случае целесообразнее использовать асинхронные АП, переключающиеся под непосредственным воздействием изменений входных информационных сигналов. Требования к частоте следования синхроимпульсов в синхронных схемах здесь заменяются требованиями к частоте изменения входных сигналов.

Однако следует заметить, что с учётом специального, как правило, избыточного кодирования и возникновения промежуточных неустойчивых состояний при переходах в асинхронных схемах можно получить даже меньшие скорости работы, чем в синхронных.

С целью повышения быстродействия рядом научных школ разрабатывается направление, связанное с проектированием самосинхронизирующихся устройств, в которых тактовые импульсы следуют с переменной частотой, зависящей от длительности реальных переходных процессов в схеме. Такие устройства получили название апериодических автоматов.

Длительность такта работы таких устройств равна реальной длительности переходного процесса и, следовательно, устройство работает на предельно возможной скорости. Изменение физических параметров схемы или изменение внешних условий не приводит к нарушению алгоритма работы автомата, а лишь изменяет скорость его работы.

Некоторые устройства принадлежат к классу автономных автоматов, которые не имеют информационных входов и под действием тактовых сигналов переходят из одного состояния в другое в соответствии с алгоритмом, определяемым структурой автомата.

По способу формирования выходных сигналов автоматы принято делить на две группы: автоматы Мили и автоматы Мура. Если функция выходов зависит только от внутреннего состояния и не зависит от состояния входов, то автомат называется автоматом Мура, в противном случае он называется автоматом Мили.

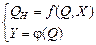– автомат Мура;

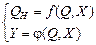– автомат Мили.

С помощью несложных процедур можно осуществить преобразование автомата Мили в автомат Мура и наоборот.

Для описания поведения автоматов Мили обычно используют пару таблиц: таблицу переходов (табл. 1) и таблицу выходов (табл. 2) [2].

Таблица 1

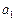
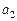
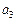
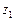
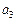
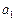
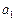
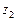
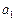
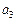
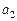
Таблица 2

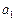
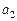
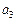
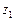
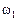
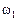
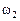
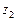
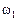
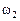
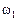
Строки указанных таблиц соответствуют входным сигналам, а столбцы – состояниям, причём крайний левый столбец обозначен начальным состоянием автомата 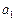. На пересечении столбца 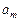и строки 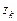в таблице переходов ставится состояние 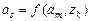, в которое автомат переходит из состояния 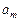под действием соответствующего входного сигнала 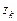, а в таблице выходов – соответствующий этому переходу выходной сигнал 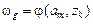. Такой способ описания АП является достаточно громоздким и неудобным для проведения дальнейших преобразований.

Так как в автомате Мура выходной сигнал зависит только от состояния, автомат Мура задаётся одной отмеченной таблицей переходов (табл. 3), в которой каждому её столбцу приписан, кроме состояния 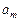, ещё и выходной сигнал 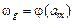, соответствующий этому состоянию.

Таблица 3

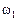
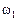
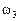
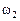
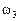
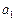
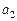
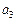
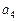
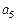
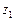
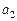
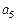
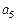
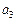
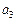
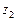
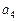
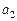
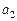
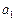
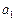
Для описания автоматов более удобно использовать совмещённую таблицу переходов и выходов, предложенную С. Ангером [1]. Эта таблица также состоит из строк и столбцов, но в данном случае столбцы соответствуют состояниям входов, а строки – текущим внутренним состояниям. Элементами таблицы переходов являются упорядоченные пары, представляющие следующие внутренние состояния и текущие выходные сигналы.

Исходное описание последовательностных схем представляется в форме таблиц переходов, имеющих одно устойчивое состояние в каждой строке. Такие таблицы называются первичными таблицами переходов. В дальнейшем эти таблицы подвергаются различным преобразованиям с целью минимизации числа внутренних состояний и устранения критических состязаний (гонок).

ПОСТРОЕНИЕ ТАБЛИЦ ПЕРЕХОДОВ АСИНХРОННЫХ АП

ДВОИЧНЫЙ СЧЁТЧИК-ДЕЛИТЕЛЬ

В качестве примера рассмотрим построение совмещённой таблицы переходов и выходов счётчика-делителя входного сигнала на 2 ( 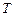-триггера). Функционирование такого устройства можно проиллюстрировать временными диаграммами, приведёнными на рис. 3.

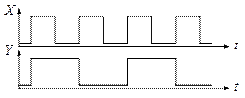
Рис. 3

Рассматриваемое устройство имеет один вход 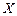и один выход 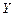. В данном случае можно говорить о том, таблица переходов будет иметь два столбца, соответствующих двум состояниям входного сигнала (0 и 1). Обозначения этих сигналов вносятся в соответствующие клетки в заголовке таблицы. О количестве строк пока никакой определённой информации нет, поскольку строки соответствуют внутренним состояниям, и эти состояния мы будем вводить по мере необходимости при построении таблицы, для того чтобы каким-то образом различить состояния схемы, возникающие в процессе её работы.

Исходное состояние (0),0. Эта пара записывается на пересечении нулевой строки и нулевого столбца. Устойчивое состояние в таблице обозначается скобками, через запятую указывается значение выходного сигнала (табл. 1). В устойчивом состоянии схема может находиться неограниченное время (до изменения входного сигнала).

Таблица 4

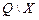
	(0),0
		(1),1
	(2),1
		(3),0

При изменении входного сигнала 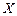с 0 на 1 (то есть при поступлении первого входного импульса) автомат переходит в новое состояние. Следующее внутреннее состояние должно быть отличным от 0, поскольку в каждой строке первичной таблицы переходов должно быть только одно устойчивое состояние. Обозначим это новое состояние цифрой 1. В таблице этот процесс изображается следующим образом: в первом столбце нулевой строки записывается номер состояния, в которое переходит автомат (1), а на пересечении первой строки и первого столбца записывается пара (1),1. Это означает, что под действием сигнала 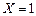схема перешла в новое устойчивое состояние и на её выходе сформировался сигнал 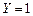. Это устойчивое состояние также будет существовать до изменения входного сигнала, поскольку рассматриваемый автомат является асинхронным (то есть он управляется входными сигналами).

При изменении входного сигнала 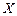с 1 на 0 (то есть при окончании входного импульса) автомат опять переходит в новое состояние, которое обозначается цифрой 2. В этом состоянии входной сигнал равен 0, а выходной – 1 (см. рис.1). В таблице это отражается следующим образом: в нулевом столбце (поскольку 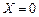) первой строки записывается номер следующего состояния автомата (2), а на пересечении второй строки и нулевого столбца записывается пара (2),1. Это означает, что под действием сигнала 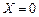схема перешла в новое устойчивое состояние, а на её выходе формируется сигнал .

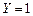При очередном изменении входного сигнала 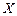с 0 на 1 (то есть при поступлении второго входного импульса) автомат опять переходит в новое состояние, которое обозначается цифрой 3. В этом состоянии входной сигнал 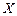равен 1, а выходной – 0 (рис. 1). В таблице это отражается следующим образом: в первом столбце (поскольку 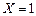) второй строки записывается номер следующего состояния автомата (3), а на пересечении третьей строки и первого столбца записывается пара (3),0. Это означает, что под действием сигнала 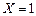схема перешла в новое устойчивое состояние и на её выходе сформировался сигнал .

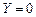При следующем изменении входного сигнала 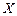с 1 на 0 (то есть при окончании второго входного импульса) автомат опять переходит в новое состояние, которое совпадает с исходным состоянием (0). В этом состоянии входной сигнал 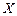равен 0 и выходной сигнал 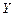тоже равен 0 (рис. 1). В таблице это отражается следующим образом: в нулевом столбце (поскольку 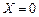) третьей строки записывается номер следующего состояния автомата (0), а на пересечении нулевой строки и нулевого столбца у нас уже записана пара (0),0. Это означает, что под действием сигнала 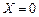схема перешла в следующее (исходное) устойчивое состояние и на её выходе формируется сигнал 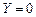. Цикл работы автомата, заданного временной диаграммой рис. 1, завершился.

Для корректного задания схемы нам необходимо определить состояние выходной функции в моменты перехода автомата из одного устойчивого состояния в другое.

В устойчивом состоянии 0 на выходе автомата формируется выходной сигнал 0 (пара (0),0 в нулевом столбце нулевой строки). В устойчивом состоянии 1 на выходе формируется сигнал 1 (пара (1),1 в первом столбце первой строки). Непосредственно в момент перехода (клетка в первом столбце нулевой строки) состояние выхода может быть любым. Ноль на выходе может смениться единицей в начале или в конце перехода, это не имеет существенного значения, поскольку время перехода практически равно времени переключения логических элементов и в данном случае им можно пренебречь. Поэтому выходной сигнал в первой клетке нулевой строки можно приравнять звёздочке (пара 1,* в табл. 5).

Таблица 5

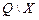
	(0),0	1,*
	2,1	(1),1
	(2),1	3,*
	0,0	(3),0

Теперь рассмотрим момент переключения из состояния 1 с выходным сигналом 1 в состояние 3, в котором выходной сигнал также должен быть равен 1. При таком переходе выходной сигнал должен быть точно определён, поскольку если мы приравняем его звёздочке, то в процессе дальнейшего синтеза эта звёздочка может доопределиться нулём и в момент перехода мы получим короткий «провал» в выходном сигнале (пара 2,1 во второй строке табл. 5). Такую ситуацию допустить нельзя, поскольку в этом случае нарушится нормальная работа заданной схемы.

Аналогично решается вопрос о значении выходного сигнала и в других клетках таблицы переходов.

Следует заметить, что вместо звёздочек в моменты переходов выходной сигнал можно приравнять тому значению, которое должно быть на выходах автомата в конце перехода, поскольку для его формирования требуется определённое время, связанное с задержками переключения выходных комбинационных схем.

ТРОИЧНЫЙ СЧЁТЧИК-ДЕЛИТЕЛЬ

Рассмотрим построение таблицы переходов счётчика-делителя частоты входного сигнала на 3, функционирование которого может быть задано временной диаграммой, приведённой на рис. 4.

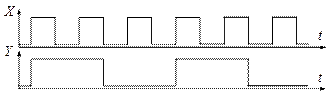
Рис.4

Таблица переходов рассматриваемого автомата может быть представлена в виде табл. 6.

Таблица 6

	(0),0	1,*
	2,1	(1),1
	(2),1	3,1
	4,*	(3),1
	(4),0	5,0
	0,0	(5),0

Вопрос о значении выходного сигнала в моменты перехода автомата из одного устойчивого состояния в другое решается аналогично случаю, рассмотренному выше при построении таблицы переходов счётчика-делителя на 2.

УПРАВЛЯЮЩИЙ АВТОМАТ ДЛЯ СВЕТОФОРА НА ПЕРЕКРЁСТКЕ НЕРАВНОЗНАЧНЫХ ДОРОГ

Светофор должен обеспечивать беспрепятственный проезд машины М, подъезжающей к перекрёстку с приоритетного направления. При этом для всех неприоритетных направлений зажигается красный сигнал светофора. При отсутствии автомобиля М на всех светофорах зажигается мигающий желтый сигнал. Перекрёсток оборудован двумя датчиками, обнаруживающими приближение машин (рис. 5):

– датчик наличия машины М, подъезжающей с приоритетного направления (лазерный луч),

– датчики наличия машин m, подъезжающих со всех неприоритетных направлений. Эти же датчики контролируют выезд машин с перекрёстка.

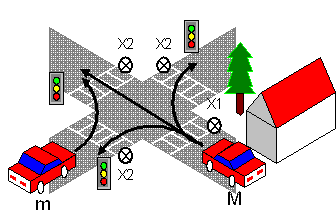
Рис. 5

Нормальное состояние светофоров – мигающий жёлтый свет (обозначим 0). Второе состояние – красный свет со всех неприоритетных направлений для проезда машины М (обозначим 1).

Исходное состояние (0),0, при котором горит мигающий жёлтый свет, никакие машины к перекрёстку не приближаются. Определим возможные устойчивые состояния схемы и соответствующие им выходные сигналы:

(1),1 – машина М находится на перекрёстке, горит красный свет для всех неприоритетных направлений;

(2),0 – машина m подъезжает к перекрёстку, машины М нет, горит жёлтый мигающий свет;

(3),1 машина М находится на перекрёстке, а m подъезжает к перекрёстку, горит красный свет;

(4),1 машина М одна подъезжает к перекрёстку;

(5),1 машины М и m одновременно подъезжают к перекрёстку.

Таблица 7

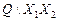
	(0),0
	(1),1
		(2),0
		(3),1
			(4),1
				(5),1

Автомат можно задать с помощью графа переходов. В этом графе состояния обозначаются кружками с цифрой (номером внутреннего состояния). Переходы показываются с помощью стрелок. Рядом с кружком указывается значение выходного сигнала АП.

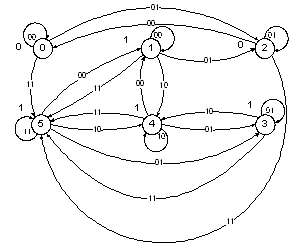
Рис. 8. Граф переходов автомата, управляющего светофором

Построение графа переходов или таблицы переходов по словесному описанию является решением задачи абстрактного синтеза конечных автоматов.

Следует заметить, что такое представление автоматов является неудобным для проведения дальнейших преобразований, особенно при большом числе внутренних состояний.

ЭЛЕМЕНТАРНЫЕ АВТОМАТЫ

Элементарным будем называть автомат, имеющий два устойчивых состояния, отличающиеся различными выходными сигналами, и хотя бы один входной сигнал, переводящий автомат из одного устойчивого состояния в другое.

Элементарный автомат имеет следующие особенности:

– ЭА является автоматом Мура и имеет два внутренних состояния;

– двум внутренним состояниям ЭА соответствуют два разных выходных сигнала, которые позволяют физически различать состояния ЭА;

– ЭА имеет несколько физических входов, на каждый из которых могут подаваться сигналы, закодированные 0 или 1.

RS-триггер

Триггеры – элементарные автоматы, содержащие собственно элемент памяти (фиксатор) и схему управления. На входы управления поступают внешние установочные сигналы. У 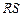-триггера таких входов два – 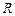и 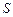. Буквой 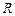латинского алфавита (от Reset) обозначен сигнал установки триггера в нуль (сигнал сброса), а буквой 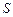(от Set) – сигнал установки в состояние логической единицы (сигнал установки). Состояние триггера совпадает со значением функции выхода 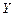и считывается по значению прямого выхода, обозначаемого как 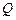. Чаще всего триггер имеет и второй выход с инверсным сигналом 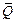(рис. 9).

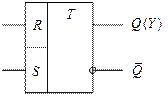
Рис. 9

Словесное описание алгоритма функционирования 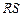-триггера может быть представлено следующим образом:

– при отсутствии сигналов 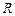и 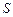триггер находится в одном из двух своих устойчивых состояний и это состояние остаётся неизменным до прихода управляющих сигналов;

– если триггер находится в нулевом состоянии и на вход 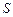подаётся активный уровень сигнала (логическая единица), то триггер переключается в единичное состояние (то есть на выходе 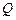устанавливается логическая единица);

– если триггер находится в нулевом состоянии и на вход 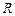подаётся активный уровень сигнала (логическая единица), то триггер не изменяет своего состояния;

– если триггер находится в единичном состоянии и на вход 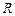подаётся активный уровень сигнала (логическая единица), то триггер переключается в нулевое состояние (то есть на выходе 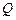устанавливается логический ноль);

– если триггер находится в единичном состоянии и на вход 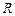подаётся активный уровень сигнала (логическая единица), то триггер не изменяет своего состояния;

– одновременная подача сигналов 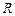и 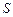не допускается (такая комбинация называется запрещённой);

По словесному описанию алгоритма функционирования строится первичная таблица переходов 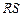-триггера (табл. 8).

Таблица 8

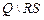
	(0),0		(0),0	*
	(1),1	(1),1		*

D-триггер

Триггер типа 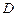(от слова Delay – задержка) имеет два входа (рис. 10). Его состояние 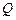повторяет входной сигнал 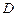, но с задержкой, определяемой тактовым сигналом 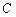(то есть состояние выхода повторяет состояние входного сигнала при наличии на входе 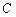активного уровня, равного логической единице).

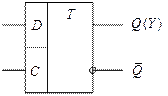
Рис. 10

По словесному описанию алгоритма функционирования строится первичная таблица переходов 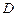-триггера (табл. 9).

Таблица 9

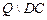
	(0),0	(0),0	(0),0
	(1),1		(1),1	(1),1

D-триггер относится к синхронным и используется для приёма информации по одному входу. Состояние логической «1» на выходе 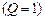, установившееся в случае 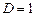и 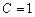, сохраняется после снятия входного сигнала до прихода очередного синхронизирующего импульса. Таким образом, D-триггер «задерживает» поступающую на его вход информацию на время, равное периоду синхронизирующих сигналов. D-триггеры используются при построении различных регистров.

У этого триггера имеется один информационный вход D и синхронизирующий вход С. Этот триггер часто называют триггером с задержкой. Слово «задержка» относится к данным, поступающим на информационный вход D. Сигнал, поступающий на этот вход, задерживается ровно на 1 такт, прежде чем появится на выходе Q (Такт – период следования тактовых импульсов С).