Методика определения надежности сложных систем с помощью минимальных путей и минимальных сечений на примере системы «2 из 3»

Этап 1. Определить для сложной системы минимальные пути и минимальные сечения

Для системы «2 из 3» (рисунок 5.7):

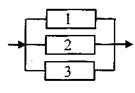
Рисунок 5.7 – Система «2 из 3»

минимальными путями будут:

1) 1, 2 2) 1, 3 3) 2, 3;

минимальные сечения:

1) 1, 2 2) 1, 3 3) 2, 3.

Этап 2. Составить некоторую фиктивную структурную схему соединения

Существует два варианта составления таких схем.

1) структурная схема составляется в виде параллельного соединения всех минимальных путей;

2) все минимальные сечения в виде блоков с параллельным соединением элементов требуется соединить последовательно.

Фиктивные схемы для системы «2 из 3» будут иметь вид:

- на основе минимальных путей (рисунок 5.8);

- на основе минимальных сечений (рисунок 5.9).

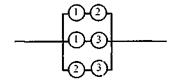
Рисунок 5.8 - Фиктивная структурная схема на основе минимальных путей

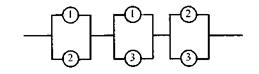
Рисунок 5.9 - Фиктивная структурная схема на основе минимальных сечений

Этап 3. Составить условные системные функции для фиктивных схем.

Условная системная функция на основе путей по рисунку 5.8 имеет следующий вид:

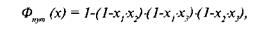(5.3)

где х_i - показатель надежности элементов, принимающий значения «да» или «нет», т.е. х_i = 1, если элемент работоспособен, и х_i = 0, если элемент отказывает;

i - номера элементов.

Условная системная функция на основе сечений по рисунку 5.9 имеет следующий вид:

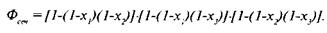(5.4)

Особенностью условной системной функции является то, что она составлена на использовании альтернативных или булевых переменных, которые могут принимать значения 1 или 0. Значит, и сама условная системная функция Ф(х) тоже может принимать значения 1 или 0. А это значит, что при решении уравнений (5.3) и (5.4) степени при х не имеют никакого значения, так как 1 и 0 в любых степенях дают все равно 1 и 0.

Преобразование (5.3) и (5.4) и удаление степеней приведет к следующему:

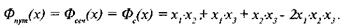(5.5)

Этап 4. Заменить условную системную функцию функцией надежности первоначальной структурной схемы технического объекта Р_с(х).

Буллевы переменные х_i заменяются соответствующими функциями P_i(t), т.е. функциями надежности элементов. После замены буллевой функции и буллевых переменных в формуле (5.5) придем к выражению следующего вида:

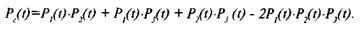(5.6)

К выражению (5.6), как мы установили, можно прийти как через минимальные пути, так и через минимальные сечения. В частном случае для системы «2 из 3», если

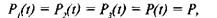(5.7)

Уравнение (5.7) приведет к знакомому выражению

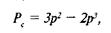(5.8)

которое было получено и методом перебора, и комбинированным методом.

Для сложных произвольных структур метод путей и сечений дает приближенную оценку надежности технической системы, причем метод путей дает верхнюю границу оценки надежности.

Лекция 6. Резервирование. Методы, способы и типы резервирования. Задачи выбора оптимального числа резервных элементов в системе