Расчет надёжности в случае ненагруженного резерва

Пусть система состоит из одного работающего элемента и (N-1) резервных (ненагруженных). Отказ системы наступает в тот момент, когда отказывает последний из N элементов.

Наработка системы до отказа:

t_c = t₁ + t₂ +……+ t_N (6.10)

Пусть все N элементов имеют одинаковое распределение наработки до отказа со средним значением t_o и дисперсией σ².

t_o = 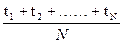(6.11)

Тогда из (6.10) следует:

M(t_c)=N·t₀;

σ²(t_c)= N·σ². (6.12)

При достаточно большом значении t_c (практически при N > 10) вероятность безотказной работы системы с ненагруженным резервом определяется следующим образом

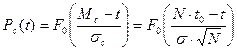. (6.13)

Пример.Пусть количество элементов с ненагруженным резервом N=9 (1 основной, 8 запасных элементов). Средняя наработка до отказа каждого элемента системы t₀=100 ч. Среднее квадратическое отклонение рассеивания случайной величины σ =50 ч.

Проанализировать изменение вероятности безотказной работы Р_с(t) системы во времени.

Решение.

Определим Р_с(t) по уравнению (6.13). Значение функции F₀(Z) определяем из справочных данных. Результаты сводим в таблицу 8.6.

;

.

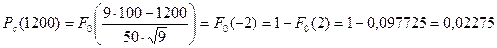Таблица 6.6 - Изменение вероятности безотказной работы системы во времени

Такие расчеты важны для определения норм запасных частей.

Из таблицы 8.6 видно, что 8 запасных частей (N=9) хватит на 600 ч. работы с довольно высокой вероятностью Р_с(t)=0,977, а на 900 ч. - только с вероятностью 0,500.

Рассчитаем норму запасных частей для заданной вероятности Р_с(t)=α.

Из формулы (6.13):

.

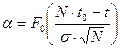где 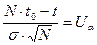- квантиль нормального распределения.

.

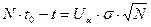Поделим обе части этого уравнения на t₀:

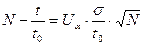
где 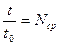- средний расход запасных изделий за время t;

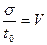- коэффициент вариации.

Тогда:

.

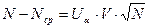Решим уравнение относительно N:

.

.

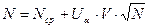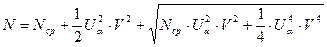. (6.14)

Расчет ненагруженного резерва более сложен, поэтому часто используют схему нагруженного резерва, но надо помнить: это приводит к заниженным значениям надежности.

Однако отметим, что рассмотренные выше методики и решения вполне могут быть использованы при выборе оптимальной схемы, так как если данный вариант имеет лучшую надежность при нагруженном резерве, то в действительности в случае ненагруженного резерва этот вариант тоже будет иметь лучшие показатели.

Лекция 7. Классификация машин и аппаратов по надежности. Работоспособность объекта: анализ области работоспособности.