Применяемые в теории надежности

Нагрузки, действующие на элементы оборудования во время эксплуатации, носят случайный характер. Случайными являются такие характеристики материалов, конкретное значение которых зависит от множества факторов. Примерами случайной величины являются наработка на отказ, интенсивность отказов, технический ресурс, срок службы машины и т.д.

Рассмотренные примеры приводят нас к понятию случайной величины.

Случайная величина – величина, которая в результате испытаний может принять значение, причем нельзя заранее предсказать, какое именно.

Случайные величины, расположенные в возрастающем порядке с указанием вероятности их появления называют распределением случайных величин.

Соотношение, устанавливающее связь между значением случайных величин и вероятностью их появления, называют законом распределения.

В процессе жизненного цикла в объекте происходят различные физические процессы. Задача теории надежности заключается в выборе такого закона распределения, который наиболее полно отражает эти физические законы.

В теории надежности используются следующие законы распределения:

1) нормальный закон распределения (закон Гаусса) применяют при изучении постепенных отказов, износа, при исследовании процессов, на изменение которых влияет большое число факторов, при определении наработки восстанавливаемых и невосстанавливаемых объектов;

2) закон распределения Вейбула-Гнеденко описывает усталостные и хрупкие разрушения, внезапные и постепенные отказы, используют при определении наработки невосстанавливаемых объектов в основном в период приработки;

3) экспоненциальный закон – частный случай распределения Вейбула-Гнеденко применяется при анализе внезапных отказов, в объектах, прошедших предварительную приработку.

Закон распределения может быть представлен в виде числовых осей, таблиц, графиков и аналитически. Законы распределения случайных величин описываются следующими функциями: отказности F(t), безотказности Р(t), интенсивности l(t). Для каждого закона распределения эти функции имеют свой вид. Функции могут пересчитываться друг в друга. Каждая из этих функций имеет свое наибольшее использование в том или ином случае.

Например l(t) имеет специфическую форму и часто используется для определения вида распределения.

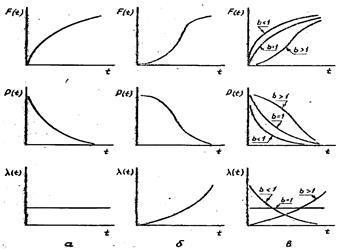
Рисунок 3.1 – Графики функций f(t), F(t), P(t), l(t) для экспоненциального (а), нормального (б), распределений и распределения Вейбула-Гнеденко (в)

Если в=1, то закон распределения Вейбулла переходит в показательный закон.

Закон Вейбулла является многопараметрическим законом.

При в =2 - 3 близок к нормальному закону.

Коэффициент вариации:

V = 0,01 – 0,3 нормальный закон используется для описания износовых отказов

V = 1 – экспоненциальный закон (для описания внезапных отказов)

V > 0,3 – закон Вейбулла

Для оценок требуемых параметров надежности производится статистическая обработка данных испытаний. Оценки параметров распределения, полученные по результатам испытаний, называются статистиками. Допустим, что при испытаниях для величины Х получен статистический ряд (результаты измерений) х1, х2, … , хn. В результате обработки экспериментальных данных определена некоторая функция q*, являющаяся функцией случайных реализаций: q* = q (х1, х2, … , хn). q* называется статистикой и является оценкой действительного значения величины Х. При выборе конкретной статистики обычно учитывают их состоятельность, эффективность и достоверность.

Так как статистическая оценка является случайной величиной, то можно указать лишь некоторую вероятность b того, что неизвестное значение величины Х действительно заключено в пределах заданной точности, т.е. b = Вер{q* - q < e}, где e - заданная точность.