Расчет на прочность открытых конических передач

Открытые конические передачи выполняют только с прямыми зубьями и применяют при окружных скоростях колес v<2 м/с. Степень точности по нормам плавности и контакта — 9-я. Размеры передачи определяют из расчета на контактную прочность зубьев с последую­щей проверкой на изгиб. При расчете принимают допускаемые напря­жения: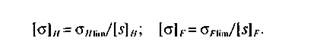

Коэффициенты внутренней динамической нагрузки K_Hv и K_Fv принимают по табл. 12.5 и 12.6.

Коэффициенты неравномерности распределения нагрузки по длине контактных линий принимают: К_нβ = K_Fβ = 1

Из-за повышенного изнашивания зубьев открытых передач значение модуля зацепления рекомендуют принимать в 1,5 раза большим, чем для закрытых передач тех же размеров.

Контрольные вопросы

1. В каких случаях применяют конические зубчатые передачи?

2. Какими достоинствами обладают конические колеса с круговыми зубьями по сравнению с прямозубыми?

3. Является ли модуль зацепления постоянной величиной для конических зубчатых колес?

4. По какому сечению зуба производят расчет на изгиб конических колес? Какой модуль характеризует размеры этого сечения?

5. Как направлены осевые силы, действующие в зацеплении конических передач?

6. Что понимают иод эквивалентным цилиндрическим колесом? Как вычисляют эквивалентные числа зубьев для конических колес, для косозубых и шевронных цилин­дрических колес?

7. Какое минимальное число зубьев допускается для шестерни цилиндрической и ко­нической передач?

8. Какое максимальное передаточное число рекомендуется для одной пары различ­ных видов зубчатых передач?

Глава 16

Планетарные зубчатые передачи

Общие сведения

Планетарныминазывают передачи, имеющие зубчатые колеса с под­вижными осями. Наиболее распространенная простая однорядная пла­нетарная передана (рис. 16.1) состоит из центрального колеса 1 с наруж­ными зубьями, неподвижного центрального колеса 3 с внутренними зубьями, сателлитов 2—колес с наружными зубьями, зацепляющихся одновременно с колесами 1 и 3 (здесь число сателлитов с = 3), и во­дила Н, на котором закреплены оси сателлитов. Водило соединено с тихоходным валом. В планетарной передаче одно колесо неподвижно (соединено с корпусом).

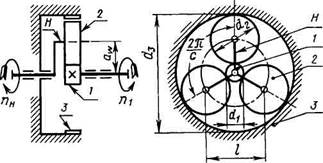
Рис. 16.1. Схема однорядной планетарной передачи

При неподвижном колесе 3 вращение колеса 1 вызывает вращение сателлита 2 относительно собственной оси, а обкатывание сателлита по колесу 3 перемещает его ось и вращает водило Н. Сателлит таким образом совершает вращение относительно водила и вместе с водилом вокруг центральной оси, т. е. совершает движение, подобное движению планет. Поэтому передачи называют планетарными.

При неподвижном колесе 3 движение передают чаще всего от коле­са/к водилу Я, можно передавать движение от водила Н к колесу 1.

В планетарных передачах применяют не только цилиндрические, но и конические колеса с прямым или косым зубом.

Если в планетарной передаче сделать подвижными все звенья, т. е. оба колеса и водило, то такую передачу называют дифференциальной.С помощью дифференциального механизма можно суммировать дви­жение двух звеньев на одном или раскладывать движение одного звена на два других. Например, в дифференциале заднего моста автомобиля движение от водила Н передают одновременно колесам 1 и 3, что позволяет при повороте одному колесу вращаться быстрее другого.

Достоинствапланетарных передач. 1. Малые габариты и масса вслед­ствие передачи мощности по нескольким потокам, численно равным числу сателлитов. При этом нагрузка в каждом зацеплении уменьша­ется в несколько раз. 2. Удобство компоновки в машинах благодаря соосности ведущего и ведомого валов. 3. Работа с меньшим шумом, чем в обычных зубчатых передачах, что связано с меньшими разме­рами колес и замыканием сил в механизме. При симметричном рас­положении сателлитов силы в передаче взаимно уравновешиваются. 4. Малые нагрузки на валы и опоры, что упрощает конструкцию опор и снижает потери в них. 5. Возможность получения больших переда­точных чисел при небольшом числе зубчатых колес и малых габаритах.

Недостатки. 1.Повышенные требования к точности изготовления и монтажа передачи. 2. Большее число деталей (подшипников), слож­нее сборка.

Планетарную передачу применяюткак: а) редуктор в силовых пере­дачах и приборах; б) коробку передач, передаточное число в которой изменяют путем поочередного торможения различных звеньев (напри­мер, водила или одного из колес); в) дифференциал в автомобилях, тракторах, станках, приборах.

Часто применяют планетарную передачу, совмещенную с электро­двигателем (мотор-редуктор, мотор-колесо).

16.2. Передаточное число планетарных передач

При определении передаточного числа планетарной передачи ис­пользуют метод остановки водила (метод Виллиса). По этому методу всей планетарной передаче мысленно сообщается дополнительное вращение с частотой вращения водила п„, но в обратном направлении. При этом водило как бы останавливается, а закрепленное колесо освобождается. Получается так называемый обращенный механизм, представляющий собой обычную непланетарную передачу, в которой геометрические оси всех колес неподвижны. Сателлиты при этом ста­новятся промежуточными (паразитными) колесами, т. е. колесами, не влияющими на передаточное число механизма. Передаточное число в обращенном механизме определяют как в двухступенчатой передаче с одним внешним и вторым внутренним зацеплением.

Здесь существенное значение имеет знак передаточного числа. Пе­редаточное число считают положительным, если в обращенном меха­низме ведущее и ведомое звенья вращаются в одну сторону, и отри­цательным, если в разные стороны. Так, для обращенного механизма передачи по рис. 16.1 имеем

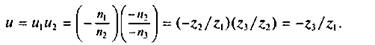
В рассматриваемом обращенном механизме знак минус показывает, что колеса 2 и 3 вращаются в обратную сторону по отношению к колесу 1. 194

16.3. Разновидности планетарных передач

Существует много различных типов планетарных передач. Наиболее широко в машиностроении применяют однорядную планетарную пере­дачу, схема которой показана на рис. 16.1. Эта передача конструктивно проста, имеет малые размеры. Находит применение в силовых и вспо­могательных приводах. КПД передачи η = 0,96...0,98 при u = 3...8.

16.4. Подбор чисел зубьев планетарных передач

Рассмотрим последовательность подбора чисел зубьев на примере получившей наибольшее распространение планетарной однорядной прямозубой передачи (см. рис. 16.1).

Число зубьев z₁ центральной шестерни 1 задают из условия неподреза­ния ножки зуба: z₁ > 17 (см. § 11.10). Принимают z₁ = 24 при Н < 350 НВ; z₁ = 21 при Н<52 HRC и z₁ = 17 при Н>52 HRC.

Число зубьев z₁ неподвижного центрального колеса 3 определяют по заданному передаточному числу и из формулы (16.2):

Число зубьев Z₂ сателлита 2 вычисляют из условия соосности, в со­ответствии с которым межосевые расстояния a_w зубчатых пар с вне­шним и внутренним зацеплениями должны быть равны. Из рис. 16.1 для немодифицированной прямозубой передачи

где d=mz — делительные диаметры.

Так как модули зацеплений планетарной передачи одинаковые, то формула (16.5) принимает вид

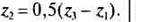
Полученные числа зубьев z₁, z₂ и г₃ проверяют по условиям сборки и соседства.

Условие сборки требует, чтобы во всех зацеплениях центральных колес с сателлитами имело место совпадение зубьев со впадинами, в противном случае собрать передачу невозможно. Установлено, что при симметричном расположении сателлитов условие сборки удовлетворя­ется, когда сумма зубьев центральных колес (z₁ + z₃) кратна числу сателлитов с = 2...6 (обычно с = 3), т. е.

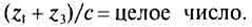
16.5. Расчет на прочность планетарных передач

Расчет на прочность планетарных передач ведут по формулам для обычных зубчатых передач. Расчет выполняют для каждого зацепления. Например, в передаче, изображенной на рис. 16.1, необходимо рассчи­тать внешнее зацепление колес 7 и 2 и внутреннее — колес 2 и 3. Так как модули и силы в этих зацеплениях одинаковы, а внутреннее за­цепление по своим свойствам прочнее внешнего, то при одинаковых материалах колес достаточно рассчитать только внешнее зацепление.

Расчет передачи ведут в последовательности, изложенной в § 13.6, со следующими отличиями.

Расчет начинают с подбора чисел зубьев колес: z₁, z₂, z₃ [см. формулы (16.4-16.9)].

При определении допускаемых напряжений (см. § 12.5) коэффици­енты долговечности Z_N и Y_H находят по числу циклов N_K перемены напряжений зубьев за весь срок службы при вращении колес только относительно друг друга.

Для центральной шестерни

(16.10)

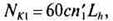
где с —число сателлитов; L_H — суммарное время работы передачи, ч; п', = n_t –п_H — относительная частота вращения центральной шестерни; n_t и п_H —частоты вращения центральной шестерни и водила, мин¹. По п', вычисляют окружную скорость, по которой выбирают степень точности передачи и коэффициенты K_Hv, K_Fv. Для сателлитов

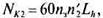
(16.11)

где n₃ — число нагружений зуба за один оборот сателлита; п'_г = п'₁ z₁/z₂ — относительная частота вращения сателлита.

Зуб сателлита за один оборот нагружается дважды — в зацеплении с колесами / и 3 (см. рис. 16.1). Однако при определении числа циклов щ = 1, так как зуб работает с колесами / и 3 разными боковыми сторонами.

При определении допускаемых напряжений изгиба [a]_F2 для зубьев сателлита вводят коэффициент Y_A, учитывающий двустороннее прило­жение нагрузки (симметричный цикл нагружения): У^ = 0,65; 0,75; 0,9 соответственно для улучшенных, закаленных ТВЧ (или цементован­ных) и азотированных сталей.

Межосевое расстояние планетарной прямозубой передачи для пары колес внешнего зацепления (центральной шестерни с сателлитом) определяют по формуле (см. § 13.4)

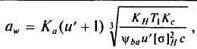
(16.12)

где и^’ - z₂/z₁ — передаточное число рассчитываемой пары колес; К_с= 1,1... 1,2 — коэффициент неравномерности распределения нагрузки между сателлитами; Г, — вращающий момент на валу центральной ше­стерни, Нм; с —число сателлитов; ψ_ba — коэффициент ширины венца колеса: ψ_ba = 0,4 для Н< 350 НВ,ψ_ba = 0,315при 350 НВ<Н<50 HRC,ψ_ba = 0,25 для Н>50 HRC.

Ширина Ь_ъ центрального колеса 3 определяется по формуле b_} = y_baa_w.

Ширину Ь_г венца сателлита принимают на 2...4 мм больше значе­ния Ь_ъ, ширина центральной шестерни b_t = l,lb₂.

Модуль зацепления

(16.13)

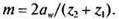
Полученный расчетом модуль округляют до ближайшего стандарт­ного значения (см. табл. 11.1),а затем уточняют межосевое расстояние:

(16.14)

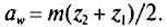
Делительный диаметр центральной шестерни d_{ = mz\.

Окружную силу в зацеплении вычисляют по формуле

Радиальную силу F_r определяют по формуле (13.7). Расчет на изгиб выполняют по формуле (13.14).

16.6. Конструктивные особенности планетарных передач

На рис. 16.3 приведена распространенная конструкция планетарно­го редуктора, выполненного по схеме рис. 16.1. Редуктор удобен для компоновки машин вследствие соосности валов.

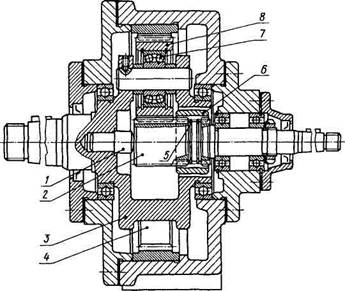
Рис. 16.3. Планетарный редуктор

Неизбежные погрешности изготовления приводят к неравномер­ному распределению нагрузки между сателлитами. Для выравнивания нагрузки по потокам в передачах с тремя сателлитами одно из цент­ральных колес делают самоустанавливающимся в радиальном направ­лении (не имеющим радиальных опор).

В конструкции на рис. 16.3 плавающей является центральная ше­стерня 2, которая самоустанавливается по сателлитам 8 в радиальном направлении (см. рис. 16.1), а в осевом направлении фиксируется шты­рем / и зубчатой муфтой 6 с установленными в ней упорными пру­жинными кольцами 5.

Для самоустановки сателлитов по неподвижному центральному колесу 4 применяют сферические подшипники качения 7.

Водила планетарных передач должны быть прочными и жесткими при малой массе. Выполняют их литыми или сварными.

На рис. 16.3 водило 3 выполнено литым из высокопрочного чугуна марки ВЧ50 за одно целое с тихоходным валом.

Контрольные вопросы

1. Какую зубчатую передачу называют планетарной? Ее устройство и принцип работы.

2. В каком случае планетарную передачу называют дифференциальной?

3. Каковы основные достоинства и недостатки планетарных передач по сравнению с обычными зубчатыми?

4. В каких областях машиностроения широко применяют планетарные передачи и по­чему?

5. Какой принцип применяют при выводе формулы для определения передаточного числа планетарной передачи?

6. В чем заключаются условия соосности, сборки и соседства планетарных передач? Почему расчет планетарных передач начинают с подбора чисел зубьев?

7. По какой частоте вращения вычисляют окружную скорость для назначения степе­ни точности передачи и выбора коэффициентов K_Hv и K_Fvl

8. Что учитывает коэффициент Y_A в формуле определения допускаемых напряжений изгиба для зубьев сателлита?

9. Почему в конструкции планетарного редуктора по рис. 16.3 центральная шестер­ня / выполнена плавающей?

Глава 17

<61626364656667>

---

Дата добавления: 2020-05-20; просмотров: 561;

---