Эквивалентное колесо

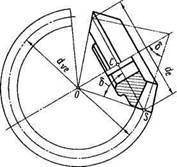
Для прямозубой передачипрофили зубьев конического колеса, по­строенные на развертке среднего дополнительного конуса (см. рис. 15.3), весьма близки к профилям зубьев эквивалентного цилиндрического прямозубого колеса. Дополнив развертку до полной окружности

(рис. 15.5), получим эквивалентное ци­линдрическое колесо с числом зубь­ев г,..

Из треугольника OCS (рис. 15.5) делительный диаметр эквивалентного колеса

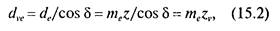
откуда эквивалентное число зубьев:

(15.3)

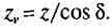
Для передачи с круговыми зубьями

профили зубьев конического колеса в нормальном сечении близки к про­филям зубьев эквивалентного цилинд­рического прямозубого колеса с числом зубьев z_v„, полученным двой­ным приведением: конического колеса к цилиндрическому и кругово­го зуба к прямому зубу [см. формулы (15.3) и (14.5)]:

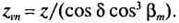
(15.4)

В формулах (15.3) и (15.4) z — действительное число зубьев кони­ческого колеса.

Силы в зацеплении

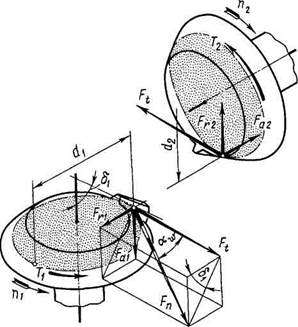
Силы в конической передаче определяют по размерам сечения на се­редине ширины зубчатого венца, в котором лежит точка приложения силы F_n, действующей перпендикулярно поверхности зуба (рис. 15.6). Силу F_n раскладывают на составляющие: F_n F_r и F_a.

В прямозубой передаче:

радиальная сила на шестерне (при а_w = 20°):

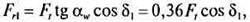
(15.5)

окружная сила на шестерне или колесе:

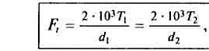
(15.6)

где Т_х и Т₂ — в Нм;d₁ d₂ — B мм.

Рис. 15.6. Схема сил в конической прямозубой передаче (колеса условно раздвинуты)

Осевая сила на шестерне:

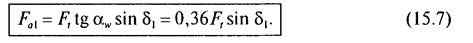
Силы на колесе соответственно равны: F_r2 = F_a1; F_a2 = F_rl.

В передаче с круговым зубомво избежание заклинивания зубьев в про­цессе зацепления при значительных зазорах в подшипниках необходимо осевую силу F_a1 на ведущей шестерне направить к основанию делитель­ного конуса. Для этого направление вращения ведущей шестерни (если смотреть со стороны вершины делительного конуса) и направление наклона зубьев должны совпадать (на рис. 11.2, б шестерня 1 вращается по ходу часовой стрелки, т. е. вправо, и зуб шестерни — правый).

В передаче с круговым зубом при соблюдении этого условия ок­ружную силу F, определяют по формуле (15.6);

радиальная сила на шестерне (при а„ = 20°; р„, = 35°)

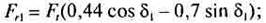
осевая сила на шестерне (при а_w = 20°; β_m=35°)

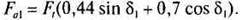
Силы на колесе соответственно равны: F_r2 = F_al; F_a2 = F_rl

(15.8)

(15.9)