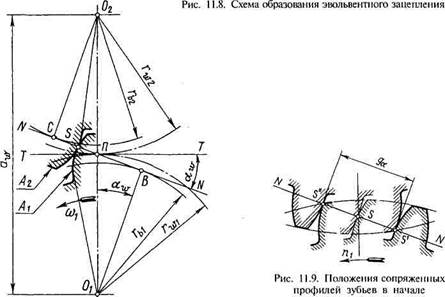
Образование эвольвентного зацепления

<36 37 383940 41 42 >

Пусть заданы межосевое расстояние a_w и передаточное число и зубчатой передачи (рис. 11.8). При известных a„ = r_wl + r_w₂ и u = r_w₂/r_wl определим радиусы начальных окружностей r_vl = a_w/(u+l), r_vl-ur_M и отметим на линии центров О_х0₂ положение полюса зацепления П.

Из центра О, опишем некоторым радиусом г_м основную окружность и, произведя ее развертку, получим эвольвентный профиль А₁зуба шестерни. На основании основной теоремы зацепления и первого свойства эвольвенты проведем через полюс П нормаль NN, которая определит точку зацепления S сопряженных профилей. Опустим из центра 0₂ перпендикуляр 0₂С на нормаль NN и радиусом r_h₂-0₂C

и конце зацепления

опишем основную окружность, развертка которой даст эвольвентный профиль А₂ зуба колеса. Построенные профили — сопряженные, так как, касаясь в точке S, они имеют общую нормаль NN. Эта нормаль касается обеих основных окружностей и является производящей прямой эвольвент обоих профилей.

При вращении колес точка зацепления S эвольвентных профилей перемещается по общей нормали NN (рис. 11.9) — геометрическому месту точек зацепления сопряженных профилей, называемому линией зацепления. Линия зацепления NN является одновременно линией давления, так как сила давления профиля зуба шестерни на профиль зуба колеса (в предположении отсутствия сил трения) действует по общей нормали NN к обоим профилям.

Угол oc_w, образованный линией зацепления NN (см. рис. 11.8) и общей касательной ТТ к начальным окружностям, называют углом зацепления.

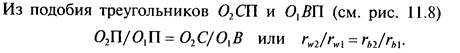
Из формулы (11.3) следует

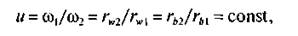
т. е. отношение угловых скоростей двух сопряженных эвольвентных профилей обратно пропорционально радиусам основных окружностей и не зависит от расстояния a_w между центрами этих окружностей.

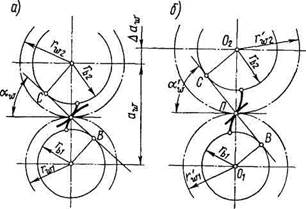
Рис. 11.10. Схема к доказательству независимости и от о„

Независимость передаточного числа и от изменения межосевого расстояния а„ можно проследить на следующем примере.

Пусть на рис. 11.10, а изображено зацепление при заданном a_w и передаточном числе и. Изменим межосевое расстояние этого зацепления до a_w + Aa_w (рис. 11.10,6). Сопоставляя рисунки, видим, что в зацеплении с расстоянием a_w + Aa„ возникли новые начальные окружности с радиусами r'_п1 и r'_w₂- Радиусы основных окружностей не изменились, так как не изменились профили зубьев, они остались очерченными теми же эвольвентами. Из подобия треугольников 0₂СП и 0,6П (рис. 11.10,6)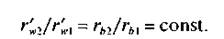

Таким образом, правильность эвольвентного зацепления не нарушается при изменении межосевого расстояния а„. Это свойство является важным преимуществом эвольвентного зацепления перед циклоидальным, весьма чувствительным к изменению расстояния а„.

<36 37 383940 41 42 >

Дата добавления: 2020-05-20; просмотров: 364;