Геометрическая прогрессия
Геометрической прогрессией называется последовательность чисел, каждый член которой, начиная со второго, равен предыдущему, умноженному на некоторое отличное от нуля число. Это число называется знаменателем прогрессии. Таким образом,
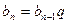
где 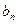 и
и 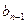 соответственно n-й и n+1-й члены прогрессии, q – знаменатель прогрессии,
соответственно n-й и n+1-й члены прогрессии, q – знаменатель прогрессии, 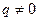 .
.
Примеры. 1) Последовательность 2, 6, 18, 54, 162, … является геометрической прогрессией со знаменателем q = 3 и первым членом 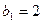 ;
;
2) Последовательность 3, -0,3, 0,03, -0,003, 0,0003, -0,00003, … является геометрической прогрессией со знаменателем q = -0,1 и первым членом 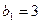 .
.
Для вычисления 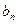 можно использовать более удобную формулу
можно использовать более удобную формулу
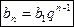 .
.
Сумма первых n членов геометрической прогрессии вычисляется по формуле
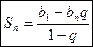 или
или 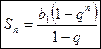 .
.
Пример 4. В геометрической прогрессии 3, 6, 12, 24, 48, … первый член 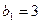 , знаменатель q = 2, найти десятый член прогрессии и сумму первых десяти членов.
, знаменатель q = 2, найти десятый член прогрессии и сумму первых десяти членов.
Решение. Десятый член прогрессии равен 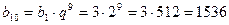 .
.
Сумма первых десяти членов равна
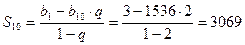 .
.
Ответ: 1536; 3069.
Пример 5. В знакочередующейся геометрической прогрессии первый член равен 3, а сумма третьего и пятого членов равна 60. Найдите второй член прогрессии.
Решение. Так как 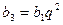 ,
, 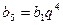 , то знаменатель прогрессии можно выразить из уравнения:
, то знаменатель прогрессии можно выразить из уравнения: 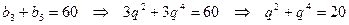 . Решим полученное биквадратное уравнение, обозначив
. Решим полученное биквадратное уравнение, обозначив 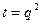 , где t>0. Корни квадратного уравнения
, где t>0. Корни квадратного уравнения 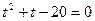 равны
равны 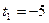 ,
, 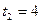 . Значение
. Значение 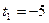 не удовлетворяет условию t>0, поэтому делаем следующую обратную замену
не удовлетворяет условию t>0, поэтому делаем следующую обратную замену 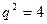 . Так как геометрическая прогрессия является знакочередующейся, то
. Так как геометрическая прогрессия является знакочередующейся, то 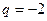 . Тогда второй член прогрессии равен
. Тогда второй член прогрессии равен 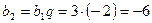 .
.
Ответ: -6.
Пример 6. Если второй член геометрической прогрессии равен 27, а пятый равен 1, то сумма пяти её первых членов равна
1) 121
2) 119
3) 108
4) 97
Решение. Так как 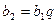 ,
, 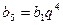 , то
, то 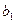 и q можно найти, решив систему:
и q можно найти, решив систему:
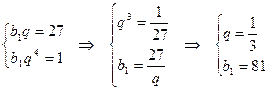
Тогда сумма пяти первых членов прогрессии равна 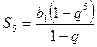 , т.е.
, т.е. 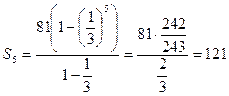 .
.
Ответ: 1).
Признак геометрической прогрессии: каждый член геометрической прогрессии, начиная со второго, есть среднее геометрическое соседних с ним членов:
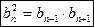 .
.
Геометрическая прогрессия, у которой 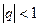 , называется бесконечной убывающей, а её сумма определяется по формуле
, называется бесконечной убывающей, а её сумма определяется по формуле
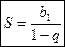 .
.
Пример 7. Последовательность 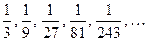 является бесконечной убывающей геометрической прогрессией, у которой
является бесконечной убывающей геометрической прогрессией, у которой 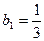 и знаменатель
и знаменатель 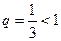 . Тогда её сумма равна
. Тогда её сумма равна
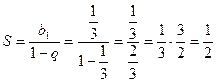 .
.
Задачи.
1. В арифметической прогрессии, второй член которой равен 7, а седьмой член равен 2, четвертый член равен
1) 3
5) -5
2) 3,5
6) 5
3) 4
7) 5,5
4) 4,5
8) -4
2. В арифметической прогрессии сумма первых трех членов равна 30, разность шестого и четвертого членов равна - 4, а n-й член равен -10. Найдите n.
1) 10
5) 20
2) 12
6) 14
3) 16
7) 18
4) 8
8) 11
9) 13
10) 25
11) 27
12)29
3. В арифметической прогрессии пятый член равен 4, сумма второго и шестого членов равна 9, а n-й член равен -1. Найдите n.
1) 9
5) 13
9) 5
2) 10
6) 7
10) 14
3) 1
7) 3
11) 20
4) 2
8) 4
12) 15
4. В арифметической прогрессии, пятый член которой равен 18, сумма первых девяти членов равна
1) 138
5) 186
2) 150
6) 198
3) 162
7) 210
4) 174
8) 222
5. В арифметической прогрессии произведение второго и пятого членов равно 45, а сумма первых пяти членов равна 35. Найдите разность прогрессии, если известно, что она положительная.
6. Десятый член арифметической прогрессии равен 19, а сумма первых пятидесяти членов равна 2500. Найдите сумму третьего, двенадцатого и двадцатого членов этой прогрессии.
7. Одиннадцатый член арифметической прогрессии равен -17, а сумма первых сорока восьми членов равна -2112. Найдите сумму третьего, тринадцатого и двадцатого членов этой прогрессии.
8. Сумма шести первых членов арифметической прогрессии меньше суммы ее последующих шести членов на 144. На сколько двадцать пятый член прогрессии больше пятнадцатого члена?
1) 10
5) 50
2) 20
6) 60
3) 30
7) 70
4) 40
8) 80
9. Сумма всех четных чисел 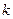 , каждое из которых делится без остатка на 15 и удовлетворяет условию
, каждое из которых делится без остатка на 15 и удовлетворяет условию 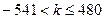 , равна
, равна
1) -960
5) 1260
9) 510
2) 1050
6) -1350
10) -1140
3) 840
7) 960
11) -1260
4) 750
8) -840
12) -1050
10. Сумма всех нечетных чисел 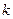 , каждое из которых делится без остатка на 17 и удовлетворяет условию
, каждое из которых делится без остатка на 17 и удовлетворяет условию 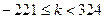 , равна
, равна
1) 255
5) -82
9) -935
2) 935
6) -877
10) 102
3) -170
7) -935
11) -102
4) 867
8) 170
12) 947
11. В арифметической прогрессии 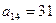 и
и 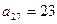 . Найдите количество отрицательных членов прогрессии, каждый из которых не меньше -25.
. Найдите количество отрицательных членов прогрессии, каждый из которых не меньше -25.
12. В арифметической прогрессии 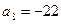 и
и 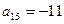 . Найдите количество неотрицательных членов прогрессии, каждый из которых меньше 40.
. Найдите количество неотрицательных членов прогрессии, каждый из которых меньше 40.
13. Если в геометрической прогрессии с положительными членами произведение второго и шестого членов равно 1, первый член равен 1/27, то знаменатель прогрессии равен
1) 3
5) 6
2) 1/3
6) 1/9
3) 1/6
7) 9
4) 2
8) 1/27
14. Знаменатель геометрической прогрессии равен -2, сумма её первых пяти членов равна 5,5. Пятый член прогрессии равен
1) 5
5) - 8
9) 1
2) 4
6) - 4
10) - 1
3) -5
7) 10
11) 12
4) 8
8) -10
12) - 3
15. Первый член геометрической прогрессии равен 150, четвертый 1,2. Найти пятый член прогрессии.
1) 1
5) 0,44
2) 0,52
6) 0,24
3) 0,5
7) 0,1
4) 0,3
8) 0,7
16. В знакочередующейся геометрической прогрессии первый член равен 12, а сумма первых трёх её членов равна 372. Найдите третий член прогрессии.
17. В знакочередующейся геометрической прогрессии первый член равен 240, а сумма третьего и пятого членов равна 75. Найдите сумму трёх первых членов прогрессии.
18. Сумма бесконечной убывающей геометрической прогрессии равна 32, а сумма её первых пяти членов равна 31. Первый член прогрессии равен
1) 121
5) 341
9) 241
2) 61
6) 71
10) 221
3) 131
7) 141
11) 361
4) 161
8) 261
12) 331
19. Найдите сумму бесконечной геометрической прогрессии с первым членом 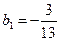 и знаменателем
и знаменателем 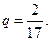
1) 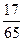
5) 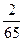
2) 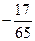
6) 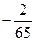
3) 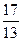
7) 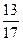
4) - 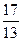
8) 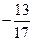
Дата добавления: 2020-05-20; просмотров: 1639;











