Понятие о правилах приближенного интегрирования.

Как известно, обводы корпуса судна не воспроизводятся аналитическими зависимостями и заданы графически теоретическим чертежом. Поэтому приведенные интегралы, определяющие элементы погруженного объема судна, не удается вычислить непосредственно.

Для их вычисления используют правила приближенного интегрирования. Из них широкое применение получили три правила - правило трапеций, правило Симпсона и правило Чебышева. При выполнении ручных расчетов наибольшее практическое применение получило правило трапеций. Рассмотрим это правило.

Вычисление определенного интеграла можно трактовать как вычисление площади ограниченной кривой, определяющей подынтегральную функцию, ее крайними ординатами и осью абсцисс (рис.20.).

Для вычисления этой площади по правилу трапеций следует разделить базу кривой L на n равных промежутков и заменить саму кривую ломаной линией, опирающейся на вершины равноотстоящих ординат. При этом ординаты кривой разбивают фигуру на трапеции, суммарная площадь которых может быть приближенно принята равной площади под кривой:

А = 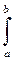у dx ≈ dL ( у₀ + у₁ + у₂ + … + у_n – (у₀ + у_n) / 2)

Величина, стоящая в круглых скобках, называется исправленной суммой ординат, а вычитаемое в этих скобках – поправкой на полусумму крайних ординат.

В качестве ординат может быть принята любая подынтегральная функция: ω, S, ωx, Sz и т.д. Тогда найденная площадь кривой будет численно равна значению данного определенного интеграла. Вычисления производят в табличной форме.

Рабочие формы вычисления определенных интегралов, выражающих элементы погруженного объема судна, приводятся в специальной литературе.

3.4.6. Кривые элементов теоретического чертежа. В процессе эксплуатации судна часто возникает потребность в быстром определении элементов теоретического чертежа для разных значений осадок. Для этой цели кривые, определяющие зависимость от осадки судна элементов погруженного объема корпуса, представляют на общем графике, который и называют кривыми элементами теоретиче-

ского чертежа (гидростатическими кривыми). Они входят в состав судовой документации и включают следующие кривые (рис. 21):

S(d) - строевая по ватерлиниям;

х_f (d)- кривая абсциссы геометрического центра площади ватерлинии;

J_x(d) - кривая поперечного момента инерции площади ватерлинии;

J_yf (d) - кривая продольного момента инерции площади ватерлинии;

V(d) - кривая объемного водоизмещения;

Δ (d) - грузовой размер;

x_с(d) - кривая абсциссы ЦВ судна;

z_c(d) -кривая аппликаты ЦВ судна;

q_см(d) - число тонн изменяющих среднюю осадку на 1 см;

α (d) -коэффициент полноты ватерлинии;

b (d) - коэффициент полноты площади мидель-шпангоута;

d(d) - коэффициент общей полноты судна.

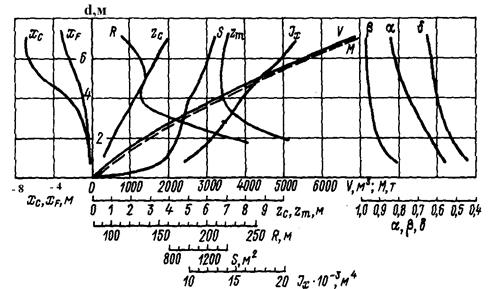
Рис.21. Кривые элементов теоретического чертежа траулера типа «Прометей»

Вместо J_x(d) и J_yf (d) или наряду с ними, строят графики r(d), R(d) и z_m(d),характеризующие изменение с осадкой судна величин

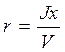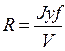; ; z_m = z_c + r,

именуемых соответственно поперечными и продольными метацентрическими радиусами, аппликатой поперечного метацентра.

Параметры r, R и z_m являются важными характеристиками остойчивости судна.

Характер кривых элементов теоретического чертежа определен формой обводов корпуса судна. Отсюда вытекают общие для всех судов черты и свойства этих кривых. Приведем несколько примеров.

Строевая по ватерлиниям S(d) (см. рис. 16) сходна по форме с мидель-шпангоутом и обладает следующими свойствами:

-площадь строевой по ватерлиниям с учетом масштаба определяет объемное водоизмещение судна V при соответствующей осадке d;

-аппликата геометрического центра этой площади определяет аппликату центра величины (ЦВ) судна z_c;

-отношение площади строевой по ватерлиниям к площади прямоугольника со сторонами d и S равно коэффициенту вертикальной полноты судна при соответствующей осадке;

-статический момент площади строевой по ватерлиниям относительно следа ОП равен с учетом масштаба статическому моменту погруженного объема судна M_xoy.

Строевая по шпангоутам ω(x) (см. рис.18) непосредственно не входит в состав кривых элементов теоретического чертежа, представленных в судовой документации. Однако элементы ее используются при построении кривой объемного водоизмещения и кривой абсциссы ЦВ судна. Строевая по шпангоутам характеризует распределение погруженного объема по длине судна и обладает следующими свойствами:

-площадь под строевой с учетом масштаба равна объемному водоизмещению судна V;

-абсцисса геометрического центра площади под строевой по шпангоутам равна абсциссе ЦВ судна x_c;

-отношение площади под строевой ω(x) к площади прямоугольника со сторонами L и B равна коэффициенту продольной полноты судна при соответствующей осадке;

-статический момент площади под строевой по шпангоутам относительно следа пл. равен с учетом масштаба статическому моменту погруженного объема М_zoy.

Кривая объемного водоизмещения V(d)(грузовой размер Δ (d)) представлена, кривой, определяющая водоизмещение судна. Порядок определения водоизмещения по осадке судна понятен из рис. 19. По ней можно решить и обратную задачу – по водоизмещению найти осадку судна.

Свойства кривой водоизмещения:

-ордината кривой с учетом масштаба равна площади под строевой по ватерлиниям соответствующей данной осадке; тангенс угла между касательной к кривой водоизмещения и осью осадок d равен соответствующей ординате строевой по ватерлиниям;

-отношение отрезка АВ на оси осадок к величине осадки ОА судна (рис.22) равно коэффициенту вертикальной полноты судна по данную ватерлинию; на рис. 22 точка В определяется пересечением касательной к кривой V(d) в точке D с осью осадок;

-площадь под кривой водоизмещения (ОДС) равна с учетом масштаба статическому моменту объема V относительно ОП М_xoy.

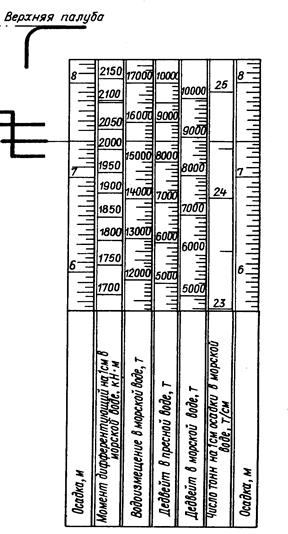Связь между водоизмещением и осадкой может быть представлена в виде номограммы (рис.23), называемой грузовой шкалой. На ее вертикальных шкалах откладываются водоизмещение в пресной и морской воде, дедвейт, осадка, число тонн на 1 см осадки (q_см), момент дифферентующий судно на 1 см (m_Д) и другие параметры. Зная одну из перечисленных величин и отметив ее на соответствующей шкале, снимают с остальных шкал искомые значения.

Необходимо помнить, что кривыми элементов теоретического

чертежа и грузовой шкалой можно пользоваться только при посадке

судна прямо и на ровный киль (Q=0, Y=0).

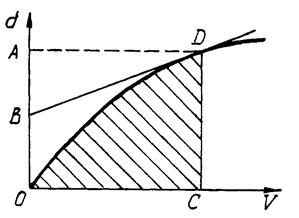
Рис.22. Грузовой размер Рис.23. Грузовая шкала