Предмет геометрической оптики (ГО)

1. ПредметГО. Раздел оптики, в котором изучаются законы распространения света на основе представлений о световых лучах, называется геометрической оптикой.

Физически луч – это направление распространения энергии ЭМ волны в пространстве. Однако в том случае, когда размеры неоднородностей в оптических средах много больше длины волны света l, а протяженность световых лучей такова, что дифракционные явления практически отсутствуют, понятие светового луча абстрагируется к прямой линии.

Таким образом, геометрическая оптика есть предельный случай реальной волновой оптики, соответствующий исчезающе малой длине световой волны по сравнению с размерами препятствий, отверстий, предметов и их изображений.

ГО не рассматривает вопрос о природе света. Ее задача состоит в математическом исследовании хода световых лучей в оптических средах с заданным коэффициентом преломления n. Законы ГО позволяют создать упрощенную, но практически достаточно точную теорию оптических систем. Она объясняет, в основном, образование оптических изображений, дает возможность вычислить аберрации оптических систем и разрабатывать методы их исправления.

Теория геометрической оптики была завершена в середине 17 века установлением принципа Ферма, из которого вытекали все известные к тому времени законы ГО.

2. ЗаконыГО. Они включают в себя 4 закона. Три первые из них были известны еще Евклиду (3 век до н.э.), а четвертый (закон преломления) был открыт в начале 17 века.

a. 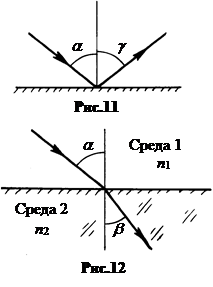Луч света в однородной среде есть прямая линия.

б. Пересекающиеся лучи не возмущают друг друга.

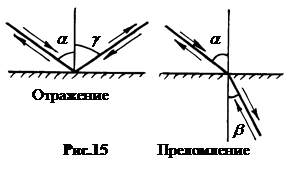
в. Угол отражения равен углу падения, а отраженный луч лежит в одной плоскости с падающим лучом и перпендикуляром, восстановленным в точку падения (закон отражения, рис.11), g = a.

г. Отношение синуса угла падения луча на границе двух прозрачных сред к синусу угла преломления обратно пропорционально отношению абсолютных показателей преломления этих сред. Преломленный луч лежит в одной плоскости с падающим лучом и перпендикуляром, восстановленным в точку падения (закон преломления, Виллеброрд Снель, 1620, Рене Декарт, 1637, рис.12).

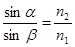. Закон преломления. (4.1)

3. ПринципФерма. В 1660 году Пьер Ферма сформулировал в виде аксиомы следующий принцип: время распространения светового луча от одной точки пространства к другой должно быть экстремальным из времен, возможных в данных условиях, то есть максимальным, минимальным или стационарным (одинаковым во всех возможных случаях).

Из принципа Ферма вытекают все законы ГО.

a. Прямолинейностьраспространениясвета. Свет распространяется в однородной среде по прямой линии, так как это кратчайшее расстояние между двумя точками. Время прохождения светом прямой минимально.

б. Законотражения. Пусть свет, идущий из точки A, с координатами x₁, y₁, отражается от поверхности в произвольной точке O с координатами x, y и попадает в точку B с координатами x₂, y₂ (рис.13).

Вопрос: где должна находится точка O, чтобы время прохождения луча из точки A в точку B с однократным отражением от поверхности было экстремальным?

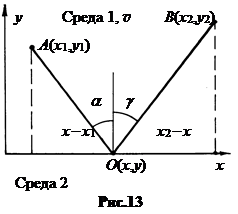Время движения луча от точки A к B есть t = (AO + OB)½v, где v – скорость света в среде 1. Из условия экстремальности времени следует:

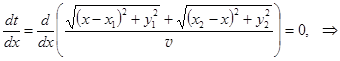
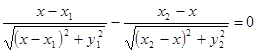. (4.2)

Или, sin a = sin g, a = g. (4.3)

Это закон отражения. Экстремальному, в данном случае минимальному времени t соответствует такое положение точки O, при котором угол отражения g равен углу падения a.

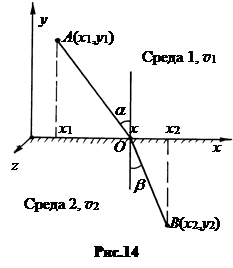в. Законпреломления. Пусть свет проходит из среды 1 в среду 2, пересекая границу раздела сред в точке O с координатами x, y (рис.14). Вопрос: где должна находится точка O, чтобы время прохождения луча от точки A до точки B было экстремальным?

Время распространения света в среде 1 есть t₁ = AOçv₁, в среде 2 есть t₂ = OBçv₂, где v₁ и v₂ – скорость света в соответствующих средах. Из условия экстремальности времени следует:

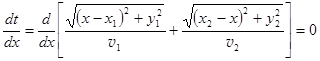. (4.4)

Отсюда ,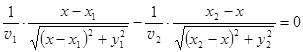

или 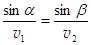. (4.5)

Если скорости света в средах v₁ и v₂ выразить через скорость света c в вакууме, v₁ = cçn₁, v₂ = cçn₂, где n₁ и n₂ – абсолютные показатели сред, то:

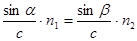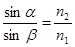, или . Это закон преломления Декарта-Снелля. (4.6)

Отношение n₂çn₁ = v₁çv₂ = n₂₁ называют относительным показателем преломления среды 2 к среде 1. Это характеристика границы раздела двух сред. Абсолютные показатели преломления двух сред n₁ и n₂ характеризуют преломление света на границе их с вакуумом.

Луч падающий, луч отраженный и луч преломленный лежат в одной плоскости с перпендикуляром, восстановленным в границе раздела в точке падения. Последнее очевидно, поскольку смещение точки O вдоль оси z приводит к удлинению пути, а значит и времени.

4. Обратимостьсветовыхлучей. Во всех явлениях отражения и преломления соблюдается закон обратимости световых лучей. Суть его в том, что при изменении направления лучей на обратное их взаимное расположение не меняется (рис.15).

Принцип обратимости сохраняется при каком угодно числе отражений и преломлений, поскольку он соблюдается при каждом из них. Поэтому принцип обратимости справедлив во всех задачах, связанных с построением изображений.

5. Полноеотражениесвета. Когда свет падает на поверхность среды с бόльшим коэффициентом преломления, какая-то его часть всегда проходит в эту более плотную среду. Если же свет падает на поверхность среды с меньшим коэффициентом преломления, то при некоторых углах падения весь свет будет отражаться обратно. Говорят, происходит полное отражение.

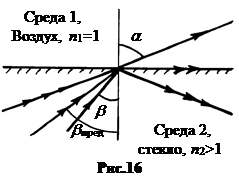Пусть изнутри стеклянного блока падает на его поверхность, граничащую с воздухом, луч света. Угол между нормалью и вышедшим из стекла лучом всегда больше, чем угол b внутри стекла (n₁ < n₂). Если увеличивать b, то при каком-то его определенном значении b_пред угол a достигнет 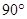(рис.16). При дальнейшем увеличении угла b > b_пред луч будет полностью отражаться обратно в стекло.

Предельный угол полного внутреннего отражения найдется из закона преломления.

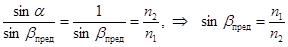. (4.7)

Таблица 4.1
Вещество		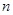bпред,˚
Алмаз	2,417
Вода	1,334
Глицерин	1,474
Лед	1,310
Орг. стекло	1,490
Сероуглерод	1,628
Спирт этиловый	1,361
Стекло разное	1,47 - 2,04	30 - 42
Эфир этиловый	1,354
Янтарь	1,532

В таблице 4.1 приведены значения показателей преломления некоторых веществ и значения предельных углов полного внутреннего отражения. С увеличением показателя преломления n предельный угол b_пред уменьшается.

Полное внутреннее отражение используется в оптических приборах для удлинения оптического пути без увеличения габаритов прибора (бинокли), для переворачивания изображений и так далее. Основным элементом здесь являются призмы полного внутреннего отражения.

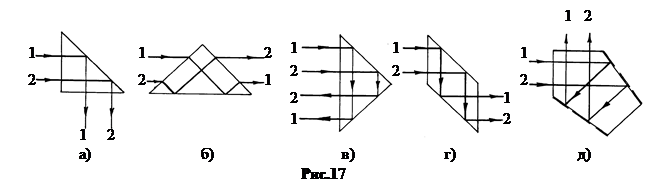На рис.17 показан ход лучей в призмах с одной отражающей гранью (а. Прямоугольная, б. Призма Дове) и ход лучей в призмах с двумя отражающими гранями (в. Прямоугольная, г. Призма – ромб, д. Пентапризма).

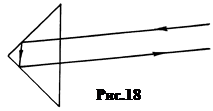Существуют призмы с тремя отражающими гранями, а так же системы призм. Множество одинаково ориентированных трехмерных призм типа «в» с прямым углом при вершине образуют катафоты (рис.18). Это оптические системы, способные в определенных угловых пределах отражать свет так, что отраженный луч выходит параллельно падающему независимо от угла падения света на грань призмы. Катафоты широко используются в автомобильном транспорте, наносятся на дорожные знаки, даже на ранцы и одежду детей.

Полное внутреннее отражение используется в волоконных световодах, представляющий собой оптически прозрачный цилиндр радиуса R₁, окруженный оболочкой радиуса R₂. Так как показатель преломления внутреннего цилиндра n₁ больше показателя преломления оболочки n₂, то запущенный в торец световой луч идет вдоль волокна, многократно отражаясь от границы раздела диэлектриков (рис.19).

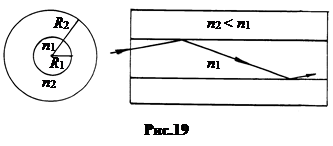В зависимости от назначения диаметр внутреннего волокна световода 2R₁ составляет от нескольких микрон до нескольких десятков микрон, а диаметр наружной оболочки – от нескольких десятков до сотен микрон. На основе волоконной оптики разрабатываются системы оптической связи, способные пропускать огромные потоки информации.

6. Преломлениелучасвета, проходящегочерезпризму. Пусть на одну грань призмы падает луч света, а из другой грани он выходит (рис.20). Угол между гранями e. Проходящий через призму луч в результате двукратного преломления на ее гранях отклоняется на угол j к основанию призмы. Угол отклонения j зависит от преломляющего угла призмы e и показателя преломления n вещества призмы.

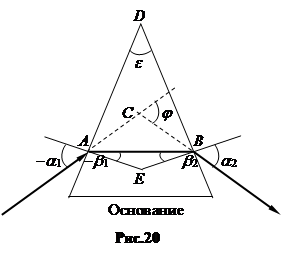Найдем связь между величинами j, e, n. Углы, отсчитываемые от нормали по часовой стрелке, считаем положительными, против часовой стрелки – отрицательными. Из DACB имеем: j = (-a₁ + b₁) + (a₂ - b₂) = (a₂ - a₁) - (b₂ - b₁) . Из фигуры ADBE следует, что e = b₂ - b₁. Подставив, получаем:

j = -a₁ + a₂ - e. (4.8)

Запишем закон преломления луча в точках A и B, полагая, что призма находится в воздухе с показателем преломления 1.

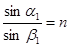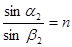, . (4.9)

Выразим отсюда a₁ и a₂ и подставим в формулу (4.8). Получаем:

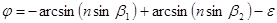. (4.10)

В формулу входят две неизвестные величины b₁ и b₂. Можно перейти к одной, подставив b₂ = b₁ - e.

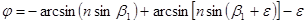. (4.11)

Исследуем j на экстремум, продифференцировав формулу (4.11) по b₁ и приравняв производную к нулю, 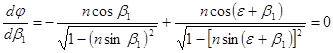. (4.12)

Условие выполняется в двух случаях: b₁ = b₁ + e, -b₁ = b₁ + e. Первое условие лишено смысла, так как e ¹ 0. Остается второе, из которого следует: - b₁ = eç2. Так как e = b₂ - b₁, то b₂ = - b₁ = eç2.

Можно показать, что экстремум соответствует минимуму j (вторая производная при - b₁ = b₂ положительна). Следовательно, при симметричном ходе луча, когда углы a₁ и a₂ одинаковы по модулю, угол отклонения луча 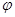минимален.

Подставив b₁ = -eç2, b₂ = eç2 в формулу (4.10), получаем:

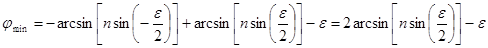. (4.13)

Или 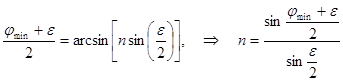. (4.14)

Поскольку показатель преломления вещества призмы n зависит от длины волны l, то прошедший сквозь призму пучок полихроматического света расщепляется в спектр. Поэтому используемые в таком качестве призмы называются спектральными или дисперсионными.

Зеркала

1. Зеркало – это гладкая поверхность, способная отражать падающие на нее лучи. В зависимости от формы поверхности различают плоские, сферические, цилиндрические, параболические и другие зеркала. Наиболее употребительны зеркала с плоской и сферической поверхностью.

2. Сферическиевогнутыезеркала. Их важнейший геометрический параметр – радиус кривизны R.

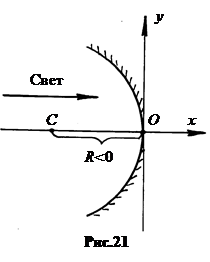
Для графического построения изображений сферическое зеркало (сегмент отражающей сферической поверхности) располагается в центре прямоугольной системы координат так, чтобы центр кривизны точка C находился на оси OX, а одна из точек поверхности – в начале системы координат в точке O (рис.21). Отражающая сторона зеркала располагается так, чтобы падающие на зеркало лучи шли в положительном направлении оси OX.

Поскольку отражающая поверхность обладает осевой симметрией относительно оси OX, то для построений достаточно сечения зеркала координатной плоскостью XOY.

Точка O, лежащая на отражающей поверхности зеркала на оси OX, называется вершиной зеркала, а ось, проходящая через вершину O и центр зеркала C – главной оптической осью зеркала. При таком расположении зеркала главной оптической осью является ось OX.

Все отрезки на оси OX, откладываемые вправо от точки O, имеют положительные значения. Аналогично, отрезки на оси OY положительны выше точки O и отрицательны ниже. Из этого правила знаков следует, что радиус кривизны вогнутого зеркала R - отрицательное число.

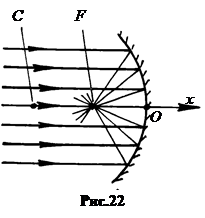
3. Фокуссферическогозеркала. Пусть на вогнутое зеркало падает пучок лучей, параллельных главной оптической оси. Если пучок параксиальный (от греч. para’ – возле, axial – ось), то есть лучи идут близко к главной оптической оси, то после отражения от зеркала все лучи параксиального пучка пересекаются в одной точке F, лежащей на главной оптической оси (рис.22). Эта точка называется главным фокусом зеркала.

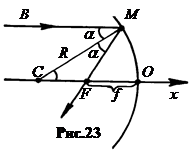
Найдем расстояние от вершины зеркала точки 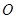до главного фокуса F. Для этого рассмотрим ход одного из лучей, параллельных оси OX (рис.23).

Пусть луч падает на зеркало в точку M. Угол a между падающим лучом и радиусом, проведенным в точку M, есть угол падения. По закону отражения угол FMC равен углу CMB.

Так как падающий луч по условию параллелен главной оптической оси OX, то углы BMC и MCF равны как накрест лежащие. Следовательно, в треугольнике FMC углы MCF и FMC одинаковы. Треугольник FMC равнобедренный. Стороны MF и FC одинаковы.

Если точку M устремить к главной оптической оси OX, то отрезок MF перейдет в пределе в отрезок OF. Отсюда следует, что отрезки OF и FC одинаковы.

Расстояние f от вершины зеркала O до главного фокуса F называют главным фокусным расстоянием зеркала. Так как отрезок OC = R есть радиус кривизны зеркала, то очевидно, что f = Rç2. Поскольку радиус кривизны вогнутого зеркала R при таких знаковых условиях отрицательное число, то и его фокусное расстояние f так же отрицательное число, R < 0, f < 0.

4. Фокальнаяплоскость. Пучок параллельных лучей, падающих на зеркало под углом y к главной оптической оси, после отражения также собирается в одной точке F', которая находится несколько в стороне от главного фокуса F (рис.24). При небольших углах y эта точка лежит в фокальной плоскости. Так называется плоскость, перпендикулярная главной оптической оси OX и проходящая через главный фокус F.

Чтобы найти построением точку F', где соберется наклонный пучок, достаточно рассмотреть один луч, тот, что проходит через центр кривизны точку C. Тогда пересечение этого луча с фокальной плоскостью и есть точка F'.

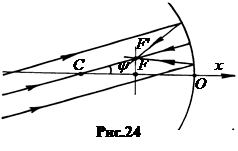
5. Формуласферическогозеркала. Пусть на главной оптической оси вогнутого зеркала находится светящаяся точка A₁. Лучи, испущенные точкой A₁, отразившись от зер-кала, пересекутся в точке A₂, находящейся на главной оптической оси (рис.25). Светящуюся точку A₁ называют предметом, а точку A₂– оптическим изображением точки A₁.

Пучок лучей, расходящийся из одной точки или сходящийся в точку, называется гомоцентрическим (от греч. homo’s – общий). Сферическое зеркало преобразует один гомоцентрический пучок в другой.

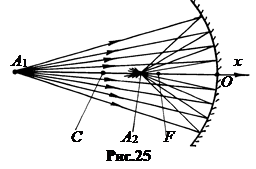
Найдем связь между тремя отрезками: расстоянием a₁ от вершины зеркала точки O до предмета A₁, расстоянием a₂ от вершины зеркала до изображения A₂ и фокусным расстоянием f. Поскольку все три отрезка с учетом принятого правила – отрицательные числа, то при записи соотношений в треугольниках будем записывать их со знаком «минус».

Выделим один произвольный луч, идущий из точки предмета A₁, и после отражения от зеркала в точке M приходящего в точку изображения A₂ (рис.26).

Рассмотрим два треугольника A₁MC и CMA₂. По теореме синусов для каждого из них запишем:

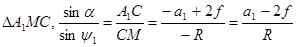, (5.1)

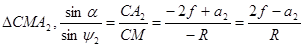, (5.2)

Разделим первое уравнение на второе.

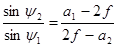(5.3)

Условие параксиальности лучей требует, чтобы углы y₁ и y₂ не превышали 5 - 7°. В этом случае с точностью до 3 знаков siny₁ = tgy₁, siny₂ = tgy₂, а точку отражения M можно полагать находящейся на оси OY. Если вертикальная координата точки M есть y, то siny₁ = tgy₁ = yç-a₁, siny₂ = tgy₂ = yç-a₂. Уравнение (5.1) принимает вид:

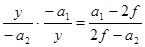, или fa₂ + fa₁ = a₁a₂ (5.4)

Разделив на произведение a₁a₂ f, получаем: 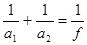. (5.5)

Это формула сферического зеркала, справедливая и с учетом правила знаков.

6. Построениеизображенийввогнутомсферическомзеркале. Пусть точка предмета B₁ не лежит на главной оптической оси. Для построения ее оптического изображения применяют обычно 3 луча. Они дают возможность построить изображение любой точки, пользуясь лишь линейкой.

Различают 3 случая: предмет находится от зеркала дальше центра кривизны точки C, предмет находится между центром кривизны точкой C и главным фокусом F и предмет находится между вершиной O и главным фокусом зеркала F.

a. Предмет A₁B₁находитсяотзеркаладальшецентракривизныточки C (иногда говорят, дальше двойного фокуса, рис.27-а).

Луч 1 идет параллельно главной оптической оси, после отражения от зеркала идет через главный фокус F.

Луч 2 идет вначале через главный фокус F, а после отражения идет параллельно главной оптической оси.

Луч 3 идет через центр кривизны C туда и обратно.

Изображение A₂B₂ полу-чается действительным (каждая точка оптического изображения образуется пересечением лучей), перевернутым, уменьшенным.

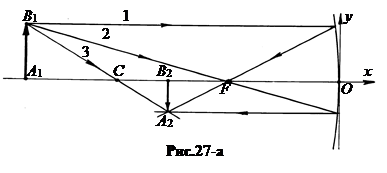
б. Предмет A₁B₁находитсямеждуглавнымфокусом F ицентромкривизны C (рис.27-б). изображение A₂B₂ получается действительным, перевернутым, увеличенным. По сравнению с первым случаем предмет и изображение меняются местами.

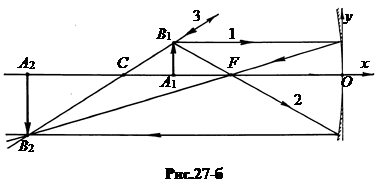
в. Предмет A₁B₁находитсямеждувершинойзеркала O иглавнымфокусом F (рис.27-в). Все три луча, вышедшие из точки B₁, после отражения от зеркала расхо-дятся и не могут нигде пересечься. Поэтому действительного изображе-ния точки они дать не могут.

Однако, если этот расходящийся пучок лучей попадает в глаз или объектив фотоаппарата, то любая оптическая система будет воспринимать этот пучок как бы вышедшим из некоторой точки B₂, находящейся на продолжении отраженных лучей за зеркалом. Такое оптическое изображение, которое образовано продолжением отраженных лучей, называют мнимым. Изображение A₂B₂ предмета в этом случае получается мнимым, прямым, увеличенным.

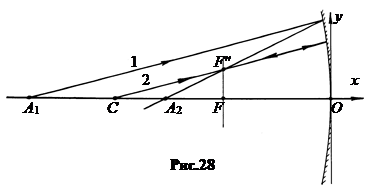г.Построениеизображенияточки A₁, лежащейнаглавнойоптическойоси, с помощью одной линейки невозможно, если пользоваться только вышедшими из этой точки лучами. Задача решается так.

Из точки предмета A₁ строит-ся произвольный луч 1 до зеркала. Затем строится параллельный вспомогательный луч 2 , идущий через центр кривизны C. Поскольку лучи параллельны, они пересекутся в фокальной плоскости. Следовательно, луч 1, отразившись от зеркала, пойдет так, что пересечется со вспомогательным лучом в фокальной плоскости (рис.28). Пересечение луча 1 с главной оптической осью дает изображение A₂.

7. 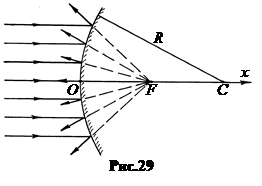Выпуклыесферическиезеркала имеют положительный радиус кривизны R > 0и мнимый фокус. Если на выпуклое зеркало падает пучок лучей, параллельных главной оптической оси, то после отражения пучок расходится, а продолжения отра-женных лучей сходятся в точке мнимого фокуса F (рис.29). Как и у вогнутого зеркала фокусное расстояние выпуклого зеркала равно f = Rç2. Поскольку R > 0, то и f – положительное число.

Формула выпуклого зеркала та же, что и для вогнутого зеркала.

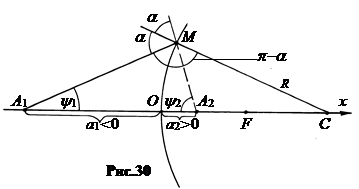Действительно, с учетом правила знаков по теореме синусов для треугольников A₁MC и CMA₂ можно записать (рис.30):

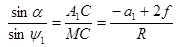, (5.5)

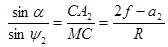, (5.6)

Разделив первое уравнение на второе, получаем:

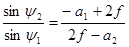. (5.7)

Из условий параксиальности лучей полагаем, что 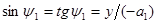, 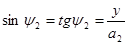. Тогда 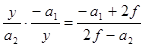. Отсюда 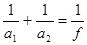. (5.8)

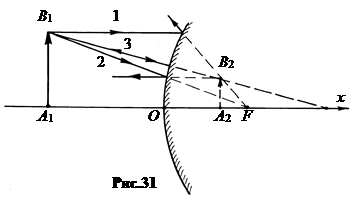При построении изображений в выпуклом зеркале при любом расстоянии от вершины до предмета реализуется только один случай. Изображение получается мнимым, прямым, уменьшенным (рис.31).

8. Плоскоезеркало можно рассматривать как частный случай сферического зеркала при R® ± ∞. В этом случае a₂ = -a₁. Изображение мнимое, прямое, натуральной величины.

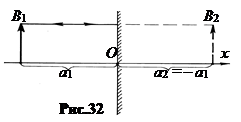Для построения изображения точки предмета достаточно одного луча, нормального зеркалу (рис.32).

Плоское зеркало – единственная оптическая система, дающая полностью не искаженное изображение при любых падающих на него лучах света. Поэтому плоские зеркала широко используются во многих оптических системах.

Тонкие линзы

1. Преломлениесветанасферическойповерхности. Пусть две среды с показателями преломления n₁ и n₂ разделяются сферической поверхностью S. Если из точки A₁, лежащей на главной оптической оси поверхности, выходит узкий гомоцентрический пучок лучей, то, преломившись на поверхности, он сходится в точке A₂ (полагаем n₂ > n₁). Найдем связь между расстоянием a₁ от предмета A₁ до вершины поверхности точки O, между расстоянием a₁ от вершины поверхности O до изображения A₂ и радиусом кривизны поверхности R.

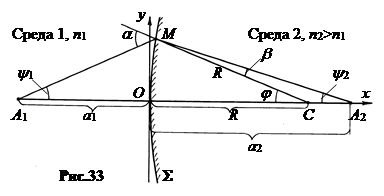
Рассмотрим один луч A₁MA₂, где M – точка на поверхности, в которой луч преломляется (рис.33). По теореме синусов в треугольниках A₁MC и MCA₂ имеем:

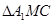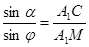, , (6.1)

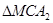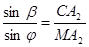, , (6.2)

Разделим 1-е уравнение на 2-е.

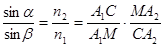. (6.3)

Полагаем пучок лучей параксиальным. В этом случае с учетом правила знаков A₁M = A₁O = -a₁, MA₂ = OA₂ = a₂, MC = OC = R, A₁C = –a₁+ R, CA₂ = a₂- R. Уравнение (6.3) принимает вид: 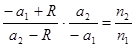. (6.4)

Избавившись от дробности и разделив на a₁a₂R, получаем: 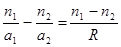. (6.5)

Это формула преломляющей сферической поверхности. Интересно, что при n₂ = - n₁ она переходит в формулу сферического зеркала.

Из формулы (6.5) следует, что любой луч, вышедший из точки A₁, при малых углах y₁ независимо от положения точки преломления M придет в одну и ту же точку A₂. Сферическая преломляющая поверхность преобразует один гомоцентрический пучок в другой.

2. Фокусысферическойпреломляющейповерхности. Если на сферическую границу падает пучок лучей, параллельных главной оптической оси, например слева, то -a₁ = ∞. Отсюда находим a₂: 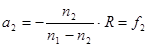. (6.6)

Если пучок падает справа, то a₂ = ∞, и 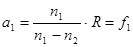. (6.7)

Величины f₁ и f₂ определяют расстояния от вершины поверхности O до точек F₁ и F₂, в которых сходятся параллельные пучки. Точки F₁ и F₂ – это фокусы преломляющей поверхности, а f₁ и f₂ – фокусные расстояния.

3. Тонкаялинза. Оптически прозрачное тело, ограниченное двумя гладкими кривыми поверхностями, называется линзой. Бывают цилиндрические, сферические, конические и другие линзы. Рассмотрим сферическую линзу с радиусами кривизны поверхностей R₁ и R₂. Полагаем, слева по рис.34 от линзы находится среда 1 с показателем преломления n₁, справа от линзы – среда 2 с показателем преломления n₂. Вещество самой линзы имеет показатель преломления n.

Полагаем линзу тонкой, то есть считаем, что толщина ее O₁O₂ мала по сравнению с радиусом кривизны поверхностей линзы R₁ и R₂. Это значит, что точки O₁ и O₂ совпадают с точкой O, называемой оптическим центром линзы.

Все лучи, проходящие через точку O, не меняют своего направления и называются осями линзы. Ось, проходящая через центры кривизны поверхностей точки c₁ и С₂, называется главной оптической осью линзы, остальные – побочными осями.

4. Формулатонкойлинзы. Найдем связь между расстоянием 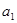от линзы до светящейся точки A₁, расстоянием a₂ от линзы до изображения этой точки A₂ и параметрами линзы R₁ и R₂ и сред n₁, n₂, n.

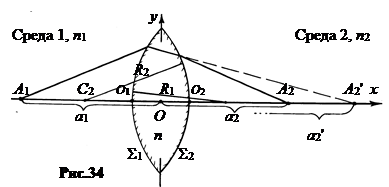Преломление лучей на первой сферической поверхности S₁ создало бы без второй сферической поверхности S₂ в сплошной среде с показателем преломления n изображение A₂' на расстоянии a₂' от вершины O. Так что из формулы (6.5) следует: 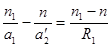.(6.8)

Для второй поверхности S₂ изображение A₂' является мнимым источником света. Построение изображения этого источника A₂' после преломления на поверхности S₂ дает точку A₂ на расстоянии a₂ от линзы. Так что можно записать:

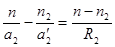. (6.9)

Просуммировав оба выражения, получаем формулу линзы. 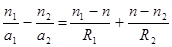. Общая формула линзы. (6.10)

5. Фокусылинзы. При падении параллельного пучка слева, когда a₁ = -∞, получаем фокусное расстояние справа от линзы f₂, а при падении пучка справа, когда a₂ = +∞, получаем фокусное расстояние f₁ слева от линзы.

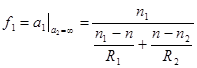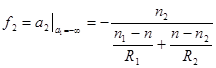, . (6.11)

В подавляющем большинстве практических случаев линза находится в однородной среде с показателем преломления n₁. Тогда n₂ = n₁, и формула линзы упрощается. Так как обычно n > n₁, то формулу удобно записать так: 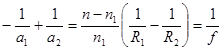. (6.12)

Здесь 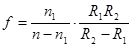- фокусное расстояние линзы. (6.13)

Если линза находится в однородной сфере, то фокусы линз слева и справа удалены на одинаковое расстояние f. Если n > n₁, то линза, более толстая в средине, называется собирающей. Ее фокусное расстояние положительно, f > 0, а фокус действительный (рис.35).

Линза, более толстая по краям, чем в середине, называется рассеивающей. Ее фокусное расстояние отрицательно, f < 0, а фокус мнимый (рис.36).

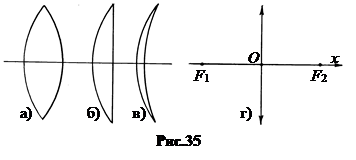На рис.35 показаны сечения разных типов собирающих линз: двояковыпуклая (а), плосковыпук-лая (б), мениск (в). На чертежах собирающие линзы изображаются отрезком со стрелками на концах и с точками главных фокусов (рис.35-г).

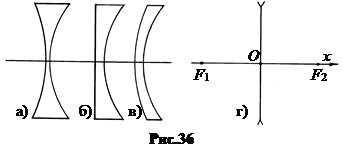Типы рассеивающих линз пока-заны на рис.36: двояковогнутая (а), плосковогнутая (б), мениск (в). Схема-тическое изображение на рис.36-г.

Величина, обратная фокусному расстоянию линзы, называется ее оптической силой 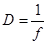. (6.14)

Единица измерений D называется диоптрия (дптр). Линза с фокусным рас-стоянием f = 1 м имеет оптическую силу D = 1 дптр, с f = 0,5 м – D = 2 дптр и так далее. У собирающих линз D > 0, у рассеивающих D < 0. Наиболее часто в диоптриях определяют оптическую силу очковых линз.

6. Построениеизображенийвсобирающихлинзах выполняется с помощью трех лучей: луча 1, проходящего через оптический центр не преломляясь, луча 2, идущего параллельно главной оптической оси, а после линзы – через задний фокус F₂, и луча 3, идущего через передний фокус F₁, а после линзы – параллельно главной оптической оси.

Различают 3 случая.

а. Предметнаходитсяотлинзыдальшедвойногофокусногорасстояния (рис.37). Изображение действительное, перевернутое, уменьшенное.

б. Предметнаходитсямеждудвойнымиглавнымфокусамилинзы(рис.38). Изображение действительное, перевернутое, увеличенное. По сравнению с первым случаем предмет и изображение меняются местами.

в. Предметнаходитсямеждуглавнымфокусомилинзой (рис.39). Изображение мнимое, прямое и увеличенное. Этот случай соответствует использованию линзы в качестве лупы.

7. 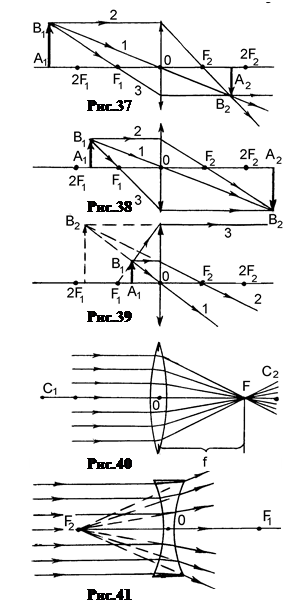Построениеизображенияврассеивающихлинзах. Пучок лучей, параллельных главной оптической оси, пройдя собирающую линзу, сходится в точке заднего главного фокуса F₂ (рис.40). Такой же пучок лучей, прошедший рассеивающую линзу, расходится. Через фокус рассеивающей линзы идут не сами лучи, а их продолжения, построенные в обратном ходу лучей направлении (рис.41). Поэтому если задний фокус F₂ собирающей линзы находится справа, то у рассеивающей линзы он находится слева. Справа находится передний фокус F₁.

Независимо от расстояния до предмета во всех случаях получается мнимое, уменьшенное, прямое изображение, расположенное между предметом и линзой (рис.42).

8. 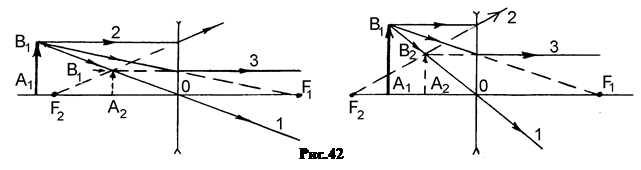Построениеизображенияточки A₁, лежащейнаглавнойоптическойоси, делается с помощью произвольного луча 1, вышедшего из точки A₁, вспомогательного параллельного луча 2, проходящего через оптический центр линзы не преломляясь. Этот вспомогательный луч 2 позволяет определить направление преломленного луча 1 после выхода из линзы.

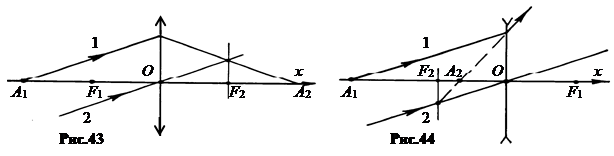В собирающей линзе луч 1 идет так, чтобы пересечься со вспомогательным в фокальной плоскости заднего фокуса (рис.43), а в рассеивающей линзе так, чтобы со вспомогательным лучом в фокальной плоскости заднего фокуса пересеклось его продолжение (рис.44).

Пересечение самого луча 1 или его продолжения с главной оптической осью и дает изображение A₂. В первом случае действительное, во втором – мнимое.

9.
Если показатель преломления вещества линзы меньше показателя преломления окружающей среды, n < n₁, то знаки фокусных расстояний меняются. Выпуклая линза становится рассеивающей (рис.45), а вогнутая – собирающей (рис.46).