Введение нового материала.
Актуализация опорных знаний и постановка проблемы.
Прочитайте выражения: (х +2у)2, (а- b)3, (c - d)2
(квадрат суммы двух выражений х и 2у; куб разности двух выражений а и b; квадрат разности двух выражений с и d.)
Что общего в заданных выражениях?
(каждый случай является какой либо степенью многочлена из двух выражений или степенью двучлена.)
Представьте каждую степень двучлена в виде многочлена. Какими формулами воспользуетесь?
Формулами квадрата суммы и разности, куба суммы

(х +2у)2 = х2 +4ху + 4у2
(а - 2)3 = а3 - 3а2 2 +3а 22 - 23= а3 - 6а2+12а -8.
Введение нового материала.
Бином Ньютона - это отношение, позволяющая представить выражение (a + b)n (n ∈ Z+) в виде многочлена.
С помощью следующей таблицы можно определить значения биномиальных коэффициентов для любой степени. Строится он следующим образом - любое число образуется суммой рядом стоящих чисел над ним. Именно потому эта таблица имеет название треугольник Паскаля.

Слева указана степень n, справа значения соответствующих биномиальных коэффициентов.
· Что означают коэффициенты перед слагаемыми?
· Столько раз эти слагаемые встретились при приведении подобных слагаемых в многочлене. Количество этих слагаемых есть не что иное, как число сочетаний С 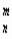 , где n - степень двучлена, m - степень второго выражения.
, где n - степень двучлена, m - степень второго выражения.
Степень одного из множителей в одночленах с3а или са3 равна 1, количество таких слагаемых, по определению сочетания, равно С 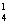 =
= 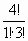 =
= 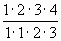 =4, что подтверждается вашими вычислениями.
=4, что подтверждается вашими вычислениями.
Проверим нашу гипотезу на слагаемом 6с2а2 : С 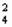 =
= 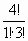 =
= 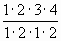 =6, что также верно.
=6, что также верно.
Заметим, что первое и последнее слагаемое стоит с коэффициентом 1, так как степень одного из выражений в этом одночлене равна 0, а по свойствам сочетаний С 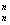 = С
= С 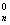 = 1.
= 1.
Объединим ваши замечания в следующие правила:
1. Каждый одночлен является произведением первого и второго выражения в различных степенях и некоторого числа;
2. Степени всех одночленов раны степени двучлена в условии;
3. Степень первого выражения одночлена в разложении убывает, начиная со степени двучлена и заканчивая нулевой;
4. Степень второго выражения одночлена в разложении возрастает, начиная с нулевой и заканчивая степенью двучлена.
5. Коэффициенты при слагаемых многочлена равны числу сочетаний С 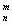 , где n - степень двучлена , m - переменная величина, пробегающая значения от 0 до n и соответствующая степени второго выражения.
, где n - степень двучлена , m - переменная величина, пробегающая значения от 0 до n и соответствующая степени второго выражения.
А теперь запишем формулу бинома Ньютона - формулу представления степени двучлена в многочлен.
Определение:
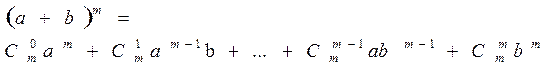
Для каждого натурального числа n и произвольных чисел a и b имеет место равенство
Равенство называется формулой бинома Ньютона, числа С 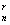 - биномиальными коэффициентами.
- биномиальными коэффициентами.
Запишем пример, используя бином Ньютона:
(х -2)5 = С 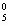 х5 + С
х5 + С 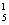 х4(-2)1 + С
х4(-2)1 + С 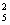 х3 (-2)2 + С
х3 (-2)2 + С 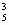 х2 (-2)3 +С
х2 (-2)3 +С 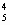 х1 (-2)4 +С
х1 (-2)4 +С 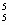 (-2)5=
(-2)5=
Посчитаем биномиальные коэффициенты, используя определение и свойства числа сочетаний:
С 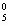 = С
= С 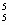 =1; С
=1; С 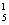 = С
= С 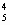 =
= 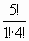 =5; С
=5; С 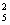 = С
= С 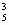 =
= 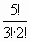 =
= 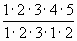 =10.)
=10.)
=х5 -5 х4 2+ 10х3 22 - 10х2 23 +5х 24-25= х5 -10х4 + 40х3 - 80х2 +80х -32.
Как видите, мы достигли того же результата, но гораздо быстрее.
| <== предыдущая лекция | | | следующая лекция ==> |
| Сущность и функции финансов. | | | Философская антропология Фейербаха |
Дата добавления: 2020-05-20; просмотров: 873;











