Почленное интегрирование и дифференцирование ряда
Мы уже видели, что из непрерывности членов сходящейся функциональной последовательности, вообще говоря, не следует непрерывность предельной функции. Аналогично, ни интегрируемость, ни дифференцируемость членов сходящегося ряда не переносится автоматически на сумму ряда. Следующие три теоремы – о функциональных свойствах предельной функции (и суммы ряда).
Теорема. Пусть 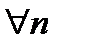 функции
функции 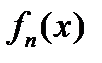 непрерывны на множестве
непрерывны на множестве 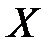 и пусть
и пусть 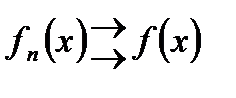 на
на 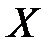 . Тогда функция
. Тогда функция 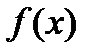 также непрерывна на
также непрерывна на 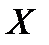 .
.
Доказательство. Требуется доказать, что 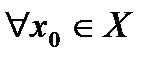 функция
функция 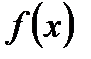 непрерывна в точке
непрерывна в точке 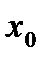 , т.е.
, т.е. 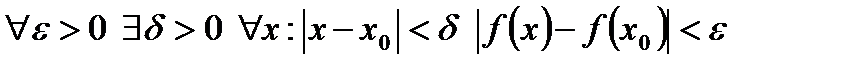 . Зафиксируем произвольное
. Зафиксируем произвольное 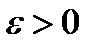 . Ввиду равномерной сходимости последовательности
. Ввиду равномерной сходимости последовательности 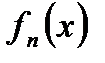
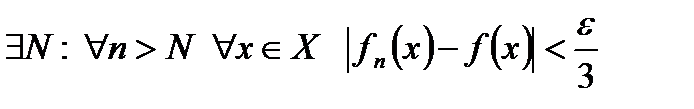 . В частности, в точке
. В частности, в точке 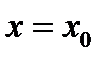 ,
, 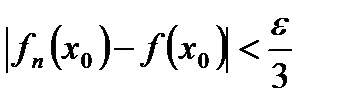 . По условию, при любом
. По условию, при любом 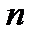 функция
функция 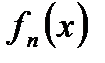 непрерывна. Значит,
непрерывна. Значит, 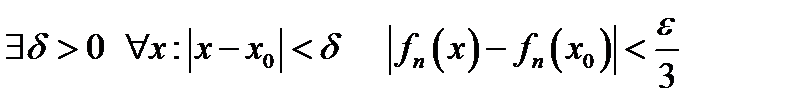 . При выбранных
. При выбранных 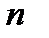 и
и 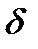 имеем:
имеем: 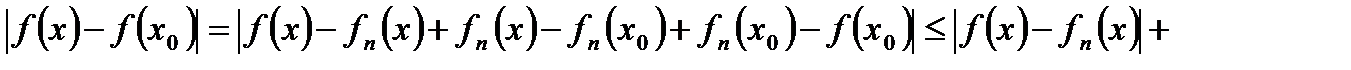
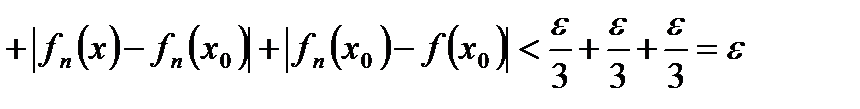 , что и требовалось доказать.
, что и требовалось доказать.
Следствие. Сумма равномерно сходящегося ряда, члены которого являются непрерывными функциями, есть непрерывная функция.
Для доказательства следует применить предыдущую теорему к последовательности частичных сумм ряда.
Приведем без доказательства две теоремы.
Теорема.(Почленное интегрирование ряда). Пусть ряд 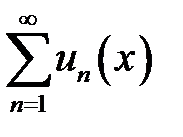 равномерно сходится к своей сумме
равномерно сходится к своей сумме 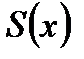 на отрезке
на отрезке 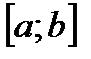 и все
и все 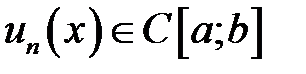 (т.е. непрерывны на отрезке
(т.е. непрерывны на отрезке 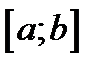 ). Тогда
). Тогда 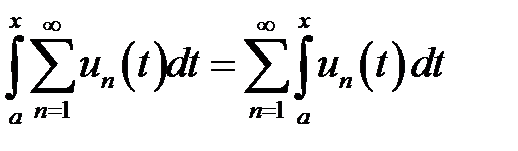 для
для 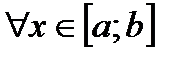 .
.
Замечание. Для функциональных последовательностей эта теорема формулируется следующим образом: Пусть 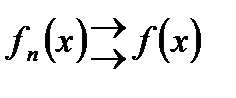 на
на 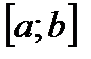 и пусть
и пусть 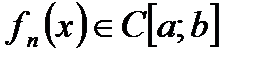 . Тогда
. Тогда 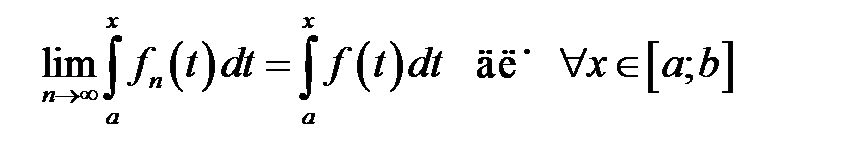 .
.
Теорема. (Почленное дифференцирование ряда).
Пусть
1. 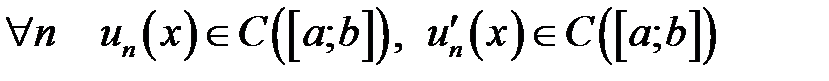 ;
;
2. Ряд 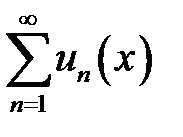 сходится на
сходится на 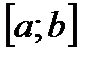 хотя бы в одной точке;
хотя бы в одной точке;
3. Ряд 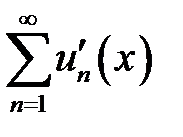 равномерно сходится на
равномерно сходится на 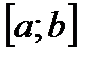 .
.
Тогда ряд 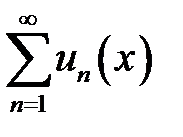 сходится на
сходится на 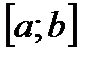 равномерно к функции
равномерно к функции 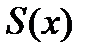 и
и 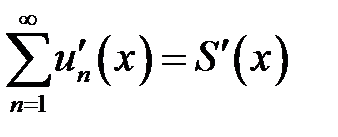 . Иными словами,
. Иными словами, 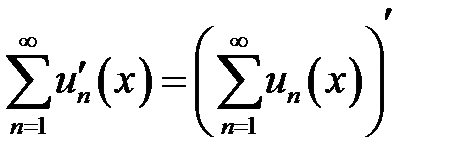 .
.
Замечание. Соответствующая теорема для последовательностей может быть сформулирована так: Пусть 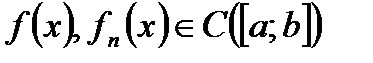 . Пусть
. Пусть 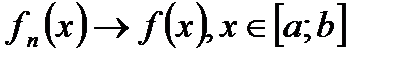 ,
, 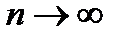 , а
, а 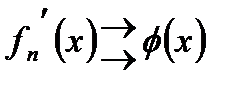 ,
, 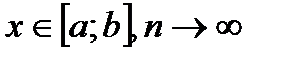 . Тогда
. Тогда 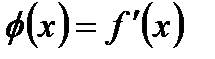 , или
, или 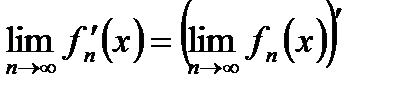 .
.
Дата добавления: 2020-05-20; просмотров: 641;











