Разложение элементарных функций в степенные ряды

Разложение .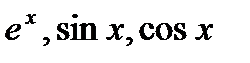

Для получения разложения 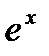заметим, что 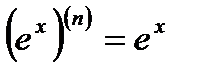, и для любого отрезка мы получаем: 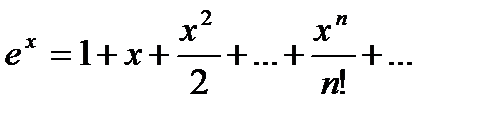. Данный ряд сходится на всей числовой оси.

Для получения разложения 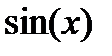заметим, что 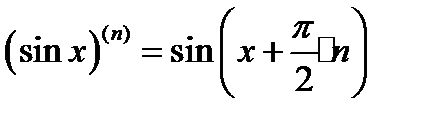, для разложения 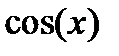производная любого порядка может быть вычислена по формуле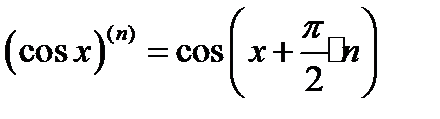

Поэтому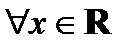

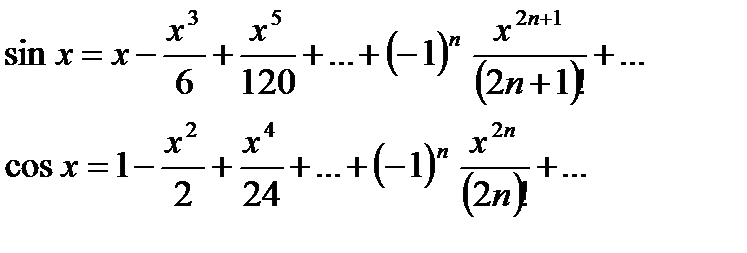
Разложение .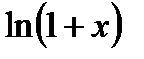

Используем равенство: 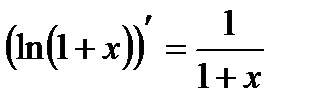. Представляя функцию 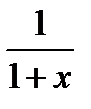как сумму бесконечной убывающей прогрессии со знаменателем 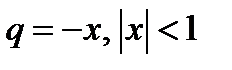: 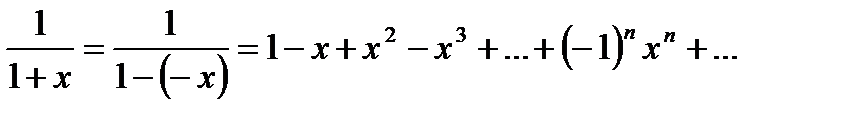. Интегрируя это разложение в пределах от 0 до 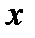, получим: 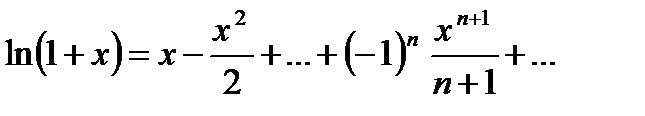. Это равенство справедливо при 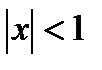. Кроме того, т.к. ряд 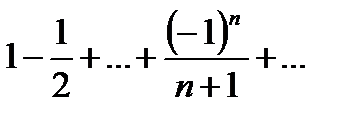сходится по теореме Лейбница, равенство сохранится и при .

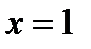Разложение .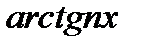

Используем равенство: 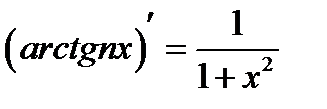. Далее, как и выше, при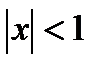 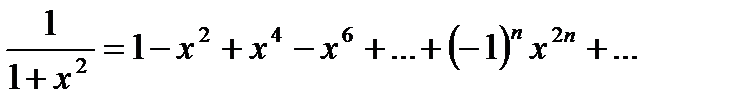. Поэтому, при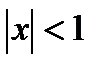 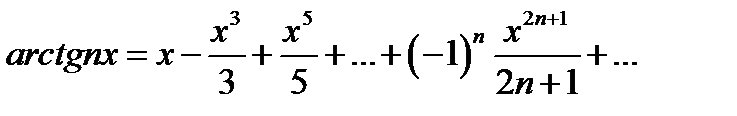. Кроме того, ряд 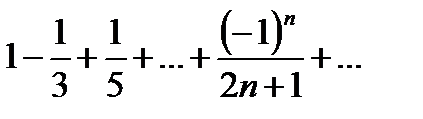сходится. Значит, написанное выше разложение имеет место и при .

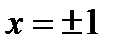Разложение бинома .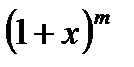

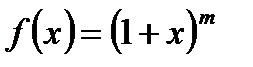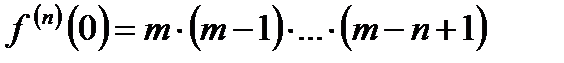Если обозначить , то . Поэтому 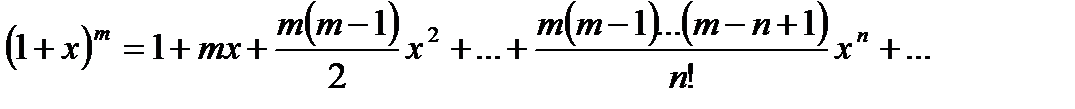. Это разложение верно для всех 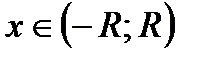, где 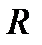- радиус сходимости. Для нахождения 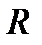используем формулу 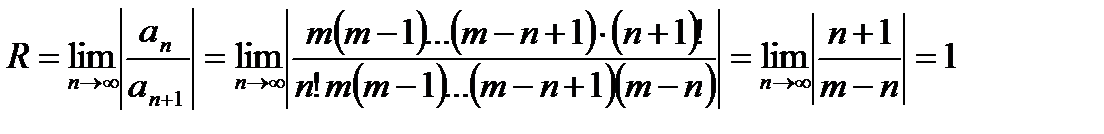. Кроме того, без доказательства, отметим, что при 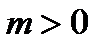разложение справедливо и при 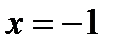, а при 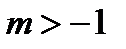- для .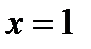

В заключение приведем несколько полезных следствий из разложения .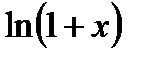

Следствие 1. Легко видеть, 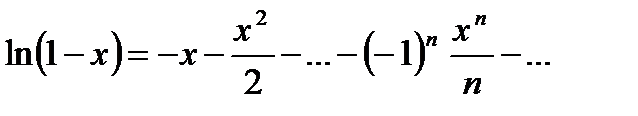. Поэтому 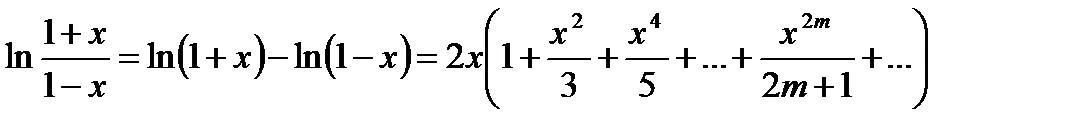при 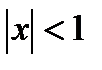. Полагая 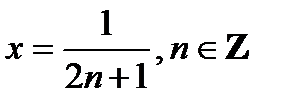, получаем, что 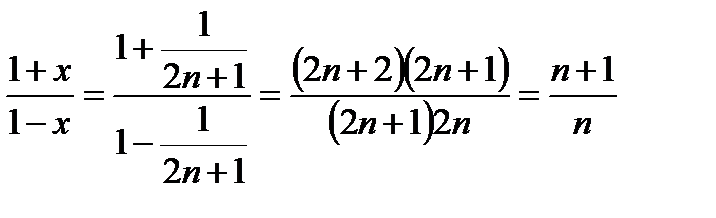и 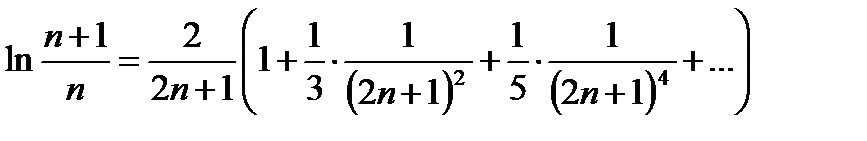. Этим разложением можно воспользоваться при вычислении логарифмов и при доказательстве формулы Стирлинга.

Следствие 2. Формула Стирлинга.

Приведем эту формулу без доказательства.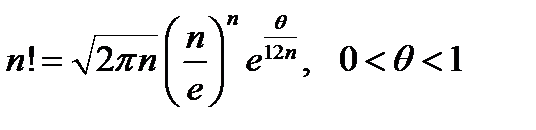

Литература

1. Ильин В.А., Позняк Э.Г. Основы математического анализа: Учебник: В 2 т. - М.: Наука, 1982. - Т.I. - 616 с.; 1983. - Т.2. - 447 с.

2. 1. Кудрявцев Л.Д. Курс математического анализа: Учебник: В 2 т. - М.: Высш. шк., 1981. - Т. I. - 687 с.; 1981. - Т.2. - 584 с.

3. Никольский С.М. Курс математического анализа: Учебник: В 2 т. - М.: Наука, 1983. - Т. I. - 464 с., 1983. - Т.2. - 448 с.

4. Смирнов В.И. Курс высшей математики: Учебник: В 3 т. -М.: Наука, 1974. - Т.I. - Ч.I. - 323 с.; Т.3. - Ч.2 - 672 с.

5. Демидович Б.П. Сборник задач и упражнений по математическому анализу. - М.: Наука, 1979. - 527 с.

6. Берман Г.Н. Сборник задач и упражнений по математическому анализу. – М. Наука, 1969. – 430 с.