Режимы движения жидкости. Физический смысл критерия Рейнольдса, его практическое значение.

В природе существуют два различных вида движения жидкости: ламинарное (от латинского слова Lamina – слой, пластина) и турбулентное (от латинского слова turbulentus - вихревой). При ламинарном движении отдельные слои жидкости скользят относительно друг друга, не смешиваясь между собой. При турбулентном или неупорядоченном движении частицы жидкости движутся по сложным, все время изменяющимся траекториям, и в жидкости происходит интенсивное перемешивание.

Уже давно известно, что вязкие жидкости (масло) движутся большей частью упорядоченно, а маловязкие жидкости (вода, воздух) – почти всегда неупорядоченно. Ясность в вопросе о том, как именно будет происходить движение жидкости в тех или иных условиях, внесена в 1883 г. в результате опытов английского физика Рейнольдса.

Опыты Рейнольдса показали, что переход от ламинарного течения к турбулентному происходит при определенной скорости, возрастающей с увеличением, вязкости и снижающейся с уменьшением диаметра трубы. Рейнольдс установил, что состояние потока жидкости в трубе (режим) зависит от безразмерного числа, которое учитывает основные факторы, определяющие это движение: среднюю скорость V, диаметр трубы d, плотность жидкости r и её динамическую вязкость m

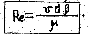Диаметр d может быть заменен любым линейным размером, связанным с условиями течения или обтекания (диаметр плавающего в жидкости шара, обтекаемой жидкостью пластинки и др.).

Число Рейнольдса, при котором происходит переход от ламинарного движения к турбулентному, называют критическим и обозначают Reкр. При Re>Reкp режим является турбулентным, при Re<Reкр - ламинарным. Критическое число Рейнольдса зависит от условий входа в трубу, шероховатости её стенок, отсутствия или наличия первоначальных возмущений в жидкости, конвективных токов и др.

Наиболее часто в расчетах принимают для критического числа Рейнольдса, при движении жидкости в трубах, значение Reкр=2000, отвечающее переходу движения жидкости из турбулентного в ламинарное; при переходе движения из ламинарного в турбулентное критическое число Рейнольдса имеет большую величину.

Критическое число Rекр увеличивается в сужающихся трубах и уменьшается в расширяющихся. Это можно объяснить тем, что при ускорении .движения частиц жидкости в сужающихся трубах их тенденция к поперечному перемешиванию уменьшается, а при замедленном течении в расширяющихся трубах усиливается.

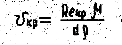По критическому числу Reкр можно найти критическую скорость, ниже которой всегда будет происходить ламинарное движение:

В трубопроводах систем отопления, водоснабжения, вентиляции, газоснабжения и др. движение, как правило, является турбулентным, так как движущаяся среда (вода, воздух, газ, пар) имеет малую вязкость. Ламинарный режим возможен лишь в трубах очень малого диаметра. Более вязкие жидкости, например масла, могут двигаться ламинарно даже в трубах большого диаметра.

С переходом .ламинарного движения в турбулентное изменяется характер распределения скоростей по сечению трубы, а также характер гидравлических сопротивлений.

При ламинарном движении распределение скоростей по сечению имеет параболический характер: непосредственно у стенок скорости равны нулю, а при удалении от них непрерывно и плавно возрастают, достигая максимума на оси трубы (рис. а). При турбулентном движении закон распределения скоростей сложнее; в большей части поперечного сечения скорости лишь незначительно меньше максимального значения (на оси), но зато вблизи стенок величина скорости резко падает в, пределах очень тонкого слоя называемого вязким или пристенным подслоем (рис. б).

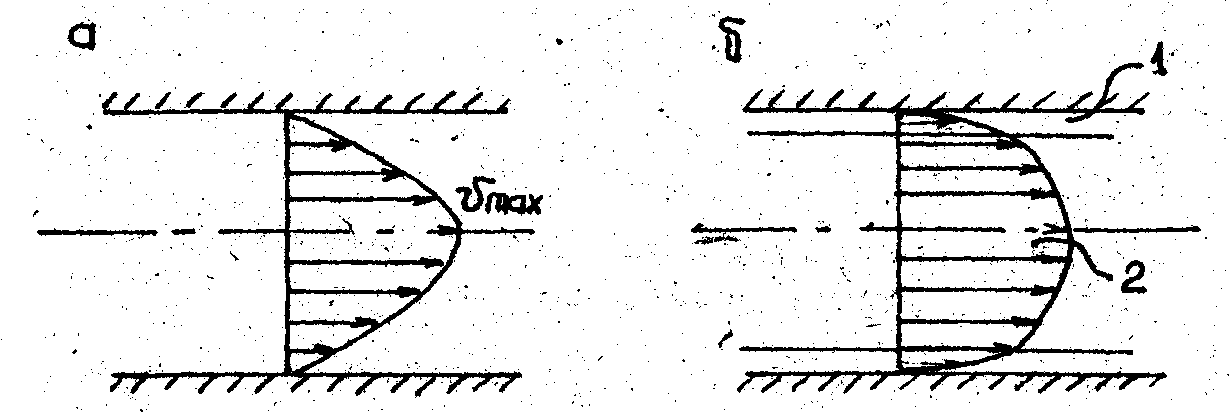Рис. Распределение скоростей при ламинарном (а) и турбулентном (б) движении жидкости в трубах: I - вязкий подслой; 2 - ядро потока

Более равномерное распределение скоростей по сечению при турбулентном движении объясняется наличием турбулентного перемешивания, осуществляемого поперечными составляющими скоростей. Благодаря этому перемешиванию, частицы с большими скоростями в центре потока и с меньшими скоростями на его периферии, непрерывно сталкиваясь, выравнивают свои скорости. У самой стенки турбулентное перемешивание парализуется наличием твёрдых границ, поэтому там наблюдается значительно более быстрое падение скорости.

Измеряя разность уровней в двух пьезометрах, присоединенных к сечениям 1-1 и 2-2 трубы постоянного диаметра, можно определить потерю напора между этими сечениями из уравнения Бернулли

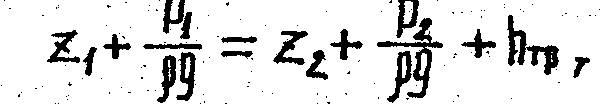откуда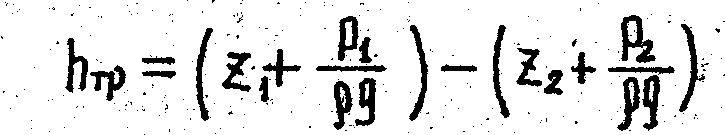

Таким образом, при равномерном движении уменьшение напора по длине трубы определяется разностью пьезометрических высот, отсчитываемых от одной и той же горизонтальной плоскости и, следовательно не зависит от расположения трубы в вертикальной плоскости.

Если пропускать воду по трубе с различной скоростью и, замерив при этом потери напора, построить кривую hтр=f(V), то она будет иметь вид представленный на рис.

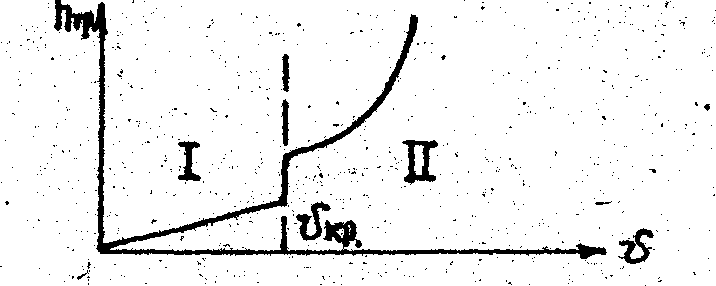Рис. Зависимость потерь напора на трение от скорости движения жидкости

До Vкр, соответствующей переходу жидкости от ламинарного движения к турбулентному, потери напора изменяются прямо пропорционально скорости (зона I), затем вид кривой изменяется, и потеря напора становятся пропорциональными более высокой степени скорости (зона II).

Следовательно, ламинарный и турбулентный режимы отличаются не только характером движения частиц (наличием поперечных скоростей при турбулентном движении), но также особенностями распределения скоростей по сечению и характером зависимости между потерями напора и скоростью.

Ламинарное движение имеет слоистый характер и происходит без перемешивания частиц. Один слой движется по другому, причем между ними возникает сила трения.

Средняя скорость при ламинарном движении жидкости в трубе равна половине максимальной. Коэффициент Кориолиса a=2, то есть кинетическая энергия ламинарного потока вдвое больше кинетической энергии, подсчитанной по средней скорости.

Потери напора на трение при ламинарном режиме пропорциональны средней скорости движения и не зависят от состояния внутренней поверхности стенок трубы, т.к. характеристика состояния стенок не входит в формулу. Это можно объяснить тем, что жидкость прилипает к стенкам, в результате чего происходит трение жидкости о жидкость, а не жидкости о стенку.

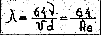Путем сопоставления формулы потерь напора на трение через гидравлический уклон, с общей зависимостью для потерь напора на трение, получим

Отсюда следует, что при ламинарном режиме коэффициент гидравлического трения обратно пропорционален числу Рейнольдса.

При достижении числом Re критического значения на контактной поверхности потока с руслом непрерывно зарождаются турбулентные возмущения в виде вихрей различного размера и различной частоты. Эти вихри отрываются от стенок русла и пронизывают толщу поступательного потока, нарушая существовавшее до того упорядоченное (послойное) движение, характерное для ламинарного режима, вызывая в нем интенсивное турбулентное перемешивание. Диффузия образовавшихся у стенки вихрей сопровождается гашением содержащейся в них кинетической энергии турбулентности, при этом механическая энергия потока частично переходит в тепловую.

В результате исследований по сопротивлению трубопроводов были предложены различные эмпирические формулы для определения коэффициента гидравлического трения.

Для вполне шероховатых труб распространена формула

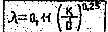Для расчетов удобна формула Альтшуля, дающая зависимость l=f(Re,Kэ/d) в явном виде: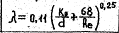

Т.к. l зависит от формы выступов, частоты, характера их расположения и т.д., то учесть влияние этих факторов непосредственно измерениями невозможно. В связи с этим в практику гидравлических расчетов было введено представление об эквивалентной равнозернистой шероховатости Кэ.

Под эквивалентной шероховатостью понимают такую высоту выступов шероховатости, сложенных из песчинок одинакового размера (шероховатость Никурадзе), которая дает при подсчетах одинаковый с заданной шероховатостью коэффициент гидравлического трения.

Таким образом эквивалентная шероховатость трубопроводов из различных материалов не определяется непосредственными измерениями высоты выступов, а находится при гидравлических испытаниях трубопроводов.