Основные задачи гидравлического расчета простого трубопровода. Особенности гидравлического расчета длинных трубопроводов.

При гидравлическом расчете трубопроводы подразделяют на простые и сложные. Простым называют трубопровод, состоящий из одной линии труб с постоянным расходом пути и передающий жидкость из резервуара в атмосферу или в другой резервуар. Сложные трубопроводы состоят из системы (сети) труб, подающей жидкость сразу в несколько точек. Сеть может быть разветвленной (разомкнутой или тупиковой), или кольцевой (замкнутой) и включать как транзитные (без раздачи жидкости по пути), так и распределительные трубопроводы.

Рассмотрим простой трубопровод, состоящий из труб одного и того же диаметра. При истечении в атмосферу уравнение Бернулли, записанное для сечений на поверхности воды в резервуаре и на выходе из трубы, имеет вид

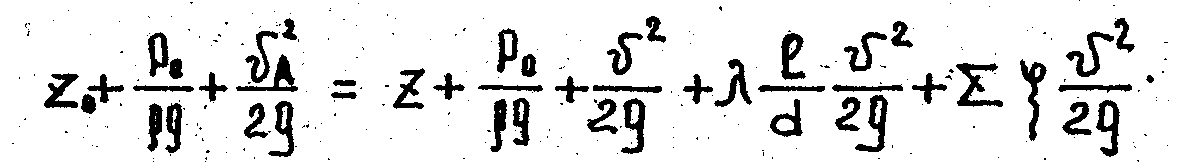Преобразовав, получим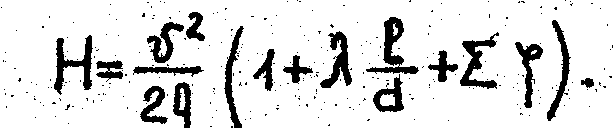

При истечении под уровень аналогично получаем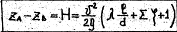

Эти формулы тождественны между собой, и гидравлические расчеты для обеих схем трубопровода будут одинаковыми. Различие состоит только в том, что при истечении под уровень единица, стоящая в скобках в пpaвой части второго уравнения представляет собой коэффициент сопротивления “на выход” потока под уровень, в то время как при истечении в атмосферу она учитывает кинетическую энергию, ocтавшуюся в потоке после выхода из трубопровода, которая может быть так или иначе использована.

Таким образом, напор H при истечении под уровень равен сумме всех сопротивлений: H=Sh_w. При истечении же в атмосферу он делится на две части: кинетическую энергию, уносимую потоком из трубы, и сумму потерь напора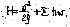

Гидравлический расчет простого трубопровода сводится к решению трех основных задач (для заданных конфигураций трубопровода, его материала и длины).

Первая задача. Требуется определить напор Н, необходимый для пропуска заданного расхода жидкости Q по заданному трубопроводу диаметром d и длиной l.

Задача решается путем непосредственного использования формулы (1) с предварительным вычислением средней скорости V=4Q/Пd².

Тогда искомый напор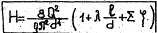

Определение значений коэффициентов l и V в данной задаче не вызывает затруднений, так как число Рейнольдса заранее известно.

Вторая задача. Требуется определить пропускную способность (расход) трубопровода, Q при условии, что известны напор H, длина трубы l и её диаметр d.

Задача решается с помощью формулы (3), согласно которой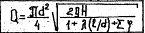

Так как коэффициенты l и V являются функциями числа Рейнольдса, которое связано с неизвестным и искомым здесь расходом Q, то решение находится методом попыток, полагая в первом приближении существование квадратичного закона сопротивления, при котором коэффициенты l и V не зависят от числа Рейнольдса.

Третья задача. Требуется определить диаметр трубопровода d при заданных расходах Q, длине трубопровода l и напоре H. Здесь Также используется формула (4), но возникают затруднения в вычислениях, так как не только неизвестно число Рейнольдса, но по отношению к искомому диаметру d мы получаем уравнение высших степеней или даже (при определении l по формуле Колбрука) трансцендентное уравнение. В связи с этим решаем задачу методом попыток, полагая в первом приближении наличие квадратичного закона сопротивления, при котором коэффициент l является функций только диаметра (при заданной шероховатости стенок трубы). Тогда уравнение (4) приводится к виду

Задаваясь рядом значений диаметра d1, d2, …,dn и вычисляя по формуле (4) соответственно ряд значений расхода Q1, Q2, …,Qn, строим график Q=f(d) (рис.), из которого определяем диаметр, отвечающий заданному расходу.

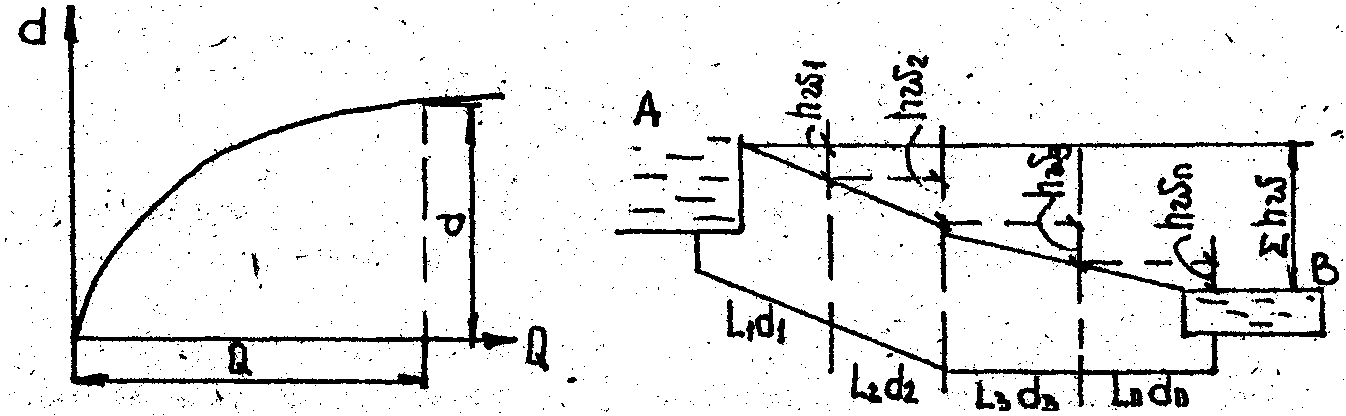Рис. 1-К расчету диаметра при заданном расходе; 2-последовательное соединение трубопроводов.

Рассмотрим простой трубопровод, составленный из труб разного диаметра (рис.), уложенных в линию одна за другой (последовательное соединение труб). Уравнение Бернулли для этого случая можно записать в виде

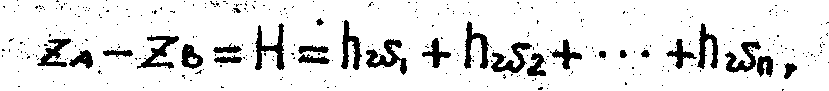
где hw1, hw2 - потери напора на первом, втором и т.д. участках трубопровода.

Потери напора на первом участке с диаметром трубы d1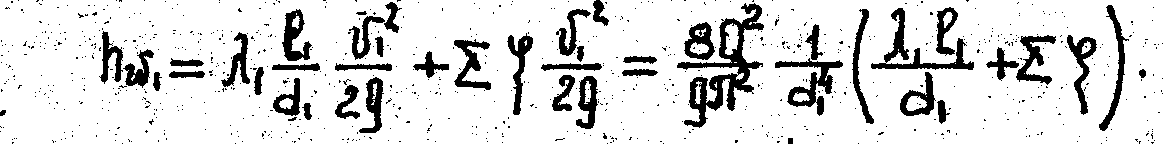

Аналогично для последующих участков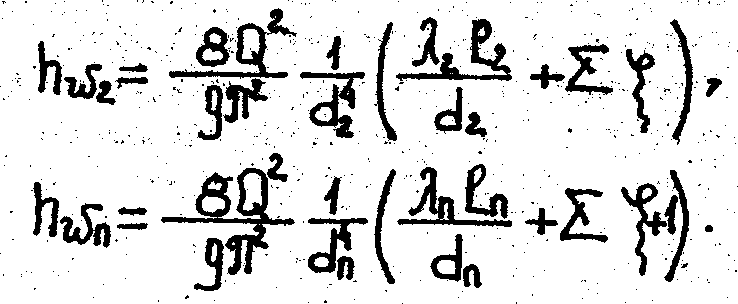

В последнем равенстве в скобках добавлено третье слагаемое - единица, учитывающая потери напора на выход.

Таким образом расчетное уравнение имеет вид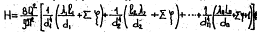

Из уравнения (5) видно, что решение первой и второй задач будет таким же, как для трубопровода постоянного диаметра. Третья же задача, если в ней есть потребность определения всех диаметров для всех участков, становится неопределенной, так как в этом случае уравнение (5) содержало бы n неизвестных. Очевидно, что для определенности решения надо задавать диаметры труб для всех участков кроме одного.

Гидравлический расчет длинных трубопроводов

В зависимости от соотношения между местными потерями напора и потерями на трение трубопроводы делятся на короткие и длинные. В длинных трубопроводах потери напора на трение во много раз превосходят потери на местные сопротивления (ll/d>>SV). Примерами длинных трубопроводов являются магистральные водопроводы, в которых местные потери напора часто составляют менее 2...3% потерь на трение и ими можно пренебречь. В коротких трубопроводах (всасывающие трубы насосных установок, трубы под насыпями; дюкеры и пр.) местные потери напора соизмеримы с потерями на трение.

Для длинных трубопроводов уравнения (1) и (2) можно записать в виде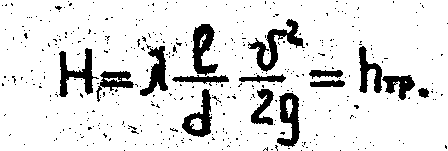

Из уравнения (6) следует, что в длинных трубопроводах весь напор практически затрачивается на преодоление сопротивлений на трение по длине.

Уравнение (3) приводится к виду

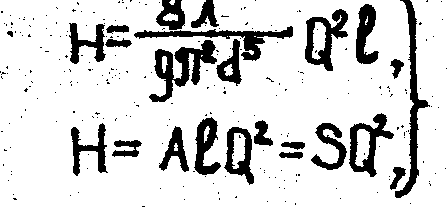(7)

а уравнение (4) к виду

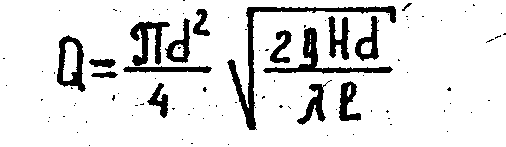
или

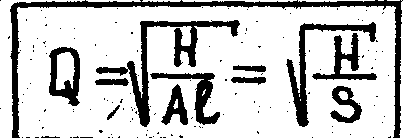(8)

где А - удельное сопротивление трубопровода,

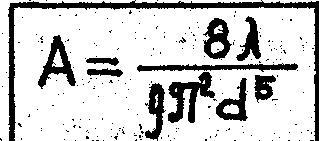
S – сопротивление трубопровода,

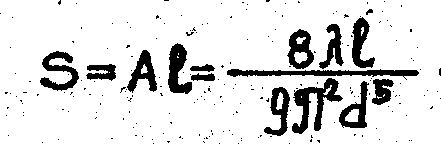
Если обозначить,

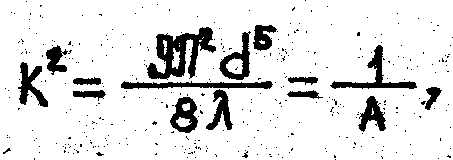
то уравнение (7) имеет вид

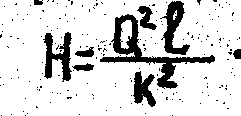(12)

Показатель К, имеющий размерность расхода называется модулем расхода или расходной характеристикой труьопровода.

Показатели A, S и К преддтавляют собой обобщенные гидравлические параметры трубопровода, использование которых значительно упрощает гидравлические расчеты.