Уравнение Бернулли для потока вязкой жидкости. Его геометрический и энергетический смысл.

Перед тем, как записать уравнение Бернулли для потока вязкой жидкости необходимо оговорить два момента. Поток жидкости отличается от элементарной струйки тем, что он имеет реальные размеры поперечного сечения, которые могут быть довольно значительных размеров. Распределение давлений и скоростей по сечению потока может быть неравномерным.

Рассмотрим распределение давления. В плоскости перпендикулярной направлению движения, гидродинамическое давление распределяется по закону гидростатики. В связи с этим справедливо условие: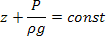

т.е. сумма отметки z и пьезометрической высоты 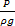во всех точках сечения потока остается одинаковой, хотя меняется для различных сечений.

В связи с тем, что распределение местных скоростей U в плоскости сечения потока неравномерно и в большинстве случаев неизвестно, то возникают трудности с определением кинетической энергии потока, т.е. с третьим слагаемым в уравнении Бернулли 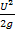. Поэтому вводим корректирующий коэффициент ±, представляющий собой отношение действительной кинетической энергии потока к кинетической энергии, подсчитанной по средней скорости в сечении. Корректив ± называется коэффициентом кинетической энергии потока или коэффициентом Кориолиса, и отражает неравномерность распределения местных скоростей по сечению потока.

Для наиболее распространенных случаев движения жидкости значения ± следующее: при ламинарном движении в круглой трубе ± = 2, при турбулентном – зависит от режима и принимает значение ± = 1,1,,,,,1,3. Обычно ± определяют опытным путем.

С учетом вышесказанного, уравнение Бернулли для потока вязкой жидкости может быть записано в виде:

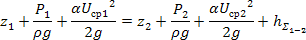где Uср1, и Uср2 – средние скорости в сечениях 1 и 2;

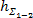– потери энергии на преодоление сопротивлений между сечениями 1 и 2.

Уравнение Бернулли устанавливает связь между скоростью движения, давления и геометрическим положением любой точки сечения потока, для которого это написано.