Первый закон термодинамики в применении к потоку движущегося газа

В технике имеется большая группа машин, в которых работа производится за счет внешней кинетической энергии рабочего тела: паровые турбины, газовые турбины, реактивные двигатели, раке­ты и др.

В процессах изменения состояния движущегося с конечной ско­ростью газа теплота расходуется не только на изменение внутрен­ней энергии и на совершение внешней работы (против внешних сил), но и на приращение внешней кинетической энергии газа при его перемещении по каналу. Поэтому уравнение первого закона термодинамики для 1 кг газа в дифференциальной форме получает следующий вид:

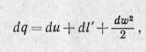(13-1)

где dq — подведенная теплота от внешних источников тепла; du — изменение внутренней энергии газа; dl' — работа против внешних сил, называемая работой про­талкивания (она не равна работе расширения газа dl);

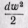— изменение внешней кинетической энергии рабочего тела.

При выводе этого уравнения не учитывалось влияние грави­тационных сил, а также считалось, что газом не совершается так называемая техническая работа (см. § 13-2).

Изменение кинетической энергии рабочего тела может происхо­дить как в трубах постоянного сечения, так и в специальных кана­лах переменного сечения, называемых соплами и диффузорами.

Если при перемещении газа по каналу происходит его расшире­ние с уменьшением давления и увеличением скорости, то такой ка­нал называют соплом.

Если в канале происходит сжатие рабочего тела с увеличением его давления и уменьшением скорости, то такой канал называют диффузором.

§ 13-2. Работа проталкивания. Дальнейшее развитие уравнения первого закона термодинамики для потока

Определим величину работы против внешних сил, или работу проталкивания. При выводе уравнения принимают следующие усло­вия истечения. Осуществляется неразрывность струи, т. е. через любое поперечное сечение канала в единицу времени протекает одинаковая масса рабочего тела:

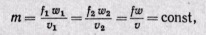(а)

где f₁, f₂, ...,f— площади поперечного сечения канала; w₁, w₂, ..., w — скорости рабочего тела; v₁, v₂, ...,v — удельные объемы.

В каждом поперечном сечении канала скорость w, давление р, температура Т и другие параметры рабочего тела постоянны по сечению канала, т. е. имеют во всех точках плоскости, пер­пендикулярной к оси трубы, одинаковое значение (осредненные величины).

Рассматривается устано­вившееся движение, называемое стационарным, т. е. не зависящим от времени. Вели­чины v, w, ρ, Т могут меняться по длине канала, но в каждом се­чении, к которому они относятся, не зависят от времени. Все ве­личины являются функцией только координат.

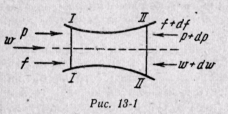
Предположим, что по каналу переменного сечения перемещается газ (рис. 13-1). Выделим сечениями / — / и // — // элементарную массу газа. В сечение / — / действует сила pf, а в сечении II — // — сила (р + dp) (f + df), действующая противоположно силе в сече­нии / — /. Обе силы в сечениях / — / и // — // совершают работу; алгебраическая сумма этих работ будет работой, затраченной на проталкивание элементарной массы газа. Элементарную работу проталкивания газа на бесконечно малом пути между сечениями / — / и // — II за 1 сек находим из уравнения

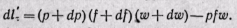
Раскрывая скобки и отбрасывая бесконечно малые величины второго и высшего порядка, получаем

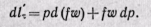(б)

Из уравнения (а) определяем

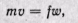
где т — секундная масса газа, протекающего через любое сечение канала в постоянном количестве.

Заменяя величину fw в уравнении (б) на mv, получаем

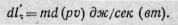
или

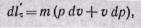
Таким образом, элементарная работа проталкивания на единицу массы равна

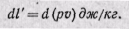(13-2)

Уравнение первого закона термодинамики в дифференциальной форме для потока газа принимает вид

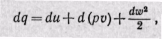
или

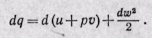
Величина в скобках (u + pv) является энтальпией, следовательно,

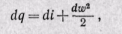(13-3)

или

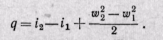
Уравнение (13-3) показывает, что подведенная теплота в процес­се при течении газа (или жидкости) расходуется на изменение внут­ренней энергии, на работу проталкивания и на изменение внешней кинетической энергии рабочего тела, или подведенная теплота при течении газа расходуется на изменение его энтальпии и внешней кинетической энергии.

Когда 1 кг движущегося газа совершает полезную работу l_т (техническую) над внешним объектом и в нем изменяется потен­циальная энергия положения (пьезометрическая высота), то закон сохранения энергии приводит к следующему уравнению:

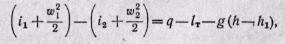(13-4)

или в дифференциальной форме

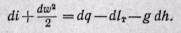
Полученное уравнение справедливо как для обратимых, так и для необратимых (происходящих с трением) процессов. Действительно, при наличии трения должна затрачиваться работа трения l_тр, которая полностью переходит в теплоту q_тр. Вследствие равенства работы трения l_тр и теплоты трения q_тр обе эти величины, имеющие различный знак, взаимно сокращаются и выпадают из уравнения (13-4). Таким образом, в случае изоэнтропного (ds = 0) течения.