Главные напряжения при прямом поперечном

Изгибе балки

Возле некоторой точки балки выделим элементарный параллелепипед 1-2-3-4 (рис.11.19,а), две грани которого расположены в поперечных сечениях балки (грани 1-2 и 3-4), а две другие грани параллельные нейтральному слою (грани 1-4 и 2-3).

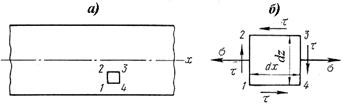
Рис. 11.19

Высота параллелепипеда равняется ширине поперечного сечения балки и расположена перпендикулярно к плоскости рисунка. На гранях параллелепипеда действуют нормальные напряжения σи касательные напряжения τ. На рис.11.19,б показаны эти напряжения, направления которых отвечают положительным знакам изгибающего момента и поперечной силы в поперечных сечениях балки. Передняя и задняя грани элементарного параллелепипеда совпадают с боковыми поверхностями балки, на которых отсутствующие нагрузки. Поэтому на этих гранях не возникают ни нормальные, ни касательные напряжения.

Если повернуть элементарный параллелепипед на некоторый угол, то напряжения на его гранях изменятся. На каждой из них будут действовать нормальные и касательные напряжения. Но существуют и такие грани (плоскости), на которых действуют только нормальные, или только касательные напряжения. Плоскости балки, в которых действуют только нормальные напряжения, называют главными плоскостями, а напряжения называют главными нормальными напряжениями. Эти напряжения имеют соответственно наибольшее и наименьшее значение σ_maxи σ_min. В случае прямого поперечного изгиба балки эти напряжения определяются по формулам, которые приводим без доведения:

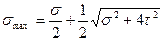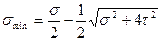и (11.22)

Существуют также взаимно перпендикулярные плоскости, на которых нормальные напряжения равняются нулю. Эти плоскости называют плоскостями сдвига. На них действуют максимальные и минимальные касательные напряжения, которые определяются по формулам:

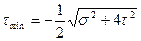, 11.23)