Изучение тенденции развития явления.
Основные вопросы: 1. Сравнительные характеристики рядов динамики.
2. Основная тенденция развития явления, методы ее изучения.
3. Сезонные колебания. Индекс сезонности.
4. Экстраполяция в рядах динамики. Условия корректности статистического прогноза.
1. Сравнительные характеристики рядов динамики. Практический интерес представляют не сами динамические ряды, а сравнение интенсивностей изменения во времени. Сравнивают ряды одинакового содержания, но относящиеся к разным территориям, организациям или сравнивают ряды разного содержания, но характеризующие один и тот же объект (например, сравнение рядов динамики, характеризующих производство важнейших видов продукции в РФ и др. странах).
Сравнительные характеристики направления и интенсивности роста, одновременно развивающихся во времени явлений определяются приведением РД к общему основанию и расчетом коэффициентов опережения.
Приведение РД к одному основанию применяется при несопоставимости цен сравниваемых стран, при расчетах сравниваемых показателей. В этом случае РД приводят к одному основанию, если нельзя решить задачу другим способом. По исходным уровням нескольких РД определяют относительные величины – базисные темпы роста или прироста. Принятый при этом за базу сравнения период времени (дата) выступает в качестве постоянной базы расчетов темпов роста для каждого из изучаемых рядов динамики. В зависимости от целей исследования базой может быть начальный, средний или другой уровень ряда.
Пример. В таблице приведены объемы производства промтоваров и базисные темпы изменения объемов производства, млн. руб.
Таблица 28
| Страна | ||||
| Россия | 168413 (1,000) | 151572 (0,900) | 128988 (0,770) | 108865 (0,650) |
| Украина | 14272 (1,000) | 1500 (1,050) | 13680 (0,960) | 11739 (0,958) |
По данным таблицы можно проследить снижение объемов производства продукции. Однако непосредственно по ним нельзя определить, в какой стране это снижение идет быстрее, т.к. различны значения абсолютных уровней этих рядов.
Приведем абсолютные уровни рядов к одному основанию, приняв за базу сравнения уровни 2000 г., и получим сравнимые показатели – базисные темпы изменения, которые показывают, что темпы снижения объемов производства продукции в России заметно превосходят соответствующие показатели Украины.
Коэффициент опережения (отставания) – показывает, во сколько раз быстрее растет (отстает) уровень одного ряда динамики по сравнению с другими и представляет собой отношение базисных темпов роста (или прироста) двух рядов динамики за одинаковые отрезки времени:
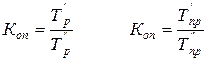
где 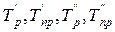 – базисные темпы роста и прироста первого и второго рядов динамики.
– базисные темпы роста и прироста первого и второго рядов динамики.
Коэффициент опережения может быть рассчитан на основе сравнения средних темпов роста (или прироста) двух динамических рядов за одинаковый период времени:
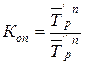 ,
,
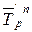 ,
, 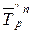 – средние темпы роста первого и второго рядов динамики соответственно;
– средние темпы роста первого и второго рядов динамики соответственно;
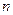 – число лет в периоде.
– число лет в периоде.
В нашем примере 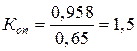 , т.е. производство продукции в РФ сокращалось в 1,5 раза быстрее.
, т.е. производство продукции в РФ сокращалось в 1,5 раза быстрее.
2. Основная тенденция развития явления, методы ее изучения. Важное значение в изучении динамики экономических процессов имеет анализ общей тенденции развития этих процессов. Постоянные факторы оказывают на изучаемые явления определяющее влияние и формируют общую тенденцию (тренд) развития. Особенность в том, что при визуальном обзоре ряда динамики общая тенденция может оказаться незаметной, поэтому нужен тщательный анализ. Например, при сильной колеблемости, рассеянности уровней членов ряда динамики основная тенденция не просматриваются.
Главными методами определения тенденции являются: метод укрупнения интервалов; метод скользящей средней; метод аналитического выравнивания.
1) Метод укрупнения интервалов ‑ это процесс преобразования периодов ряда динамики в более продолжительные (например, месячные периоды преобразуются в квартальные, квартальные в годовые и т.д.). Укрупнение интервалов при осреднении сглаживает сильные колебания уровней более коротких периодов, и тренд становится более заметным.
2) Метод скользящей средней заключается в исчислении средних из уровней рядом стоящих периодов. Они сглаживают случайные колебания. При исчислении каждой следующей скользящей средней слева один член ряда динамики отбрасывается, а справа – прибавляется, то есть:
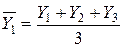 ,
, 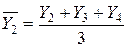 и т.д.
и т.д.
Окно осреднения выбирается из содержательных соображений, но лучше брать нечетное число, так как в этом случае скользящие средние приписываются среднему периоду времени.
Пример. Имеются следующие данные о выгрузке из вагонов картофеля. Произведен расчет определения подвижности средних путем сглаживания.
Таблица 29
| Месяц | Отгрузка, т | За квартал | В среднем за месяц | Скользящая средняя |
| Январь | 40,4 | 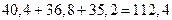
| 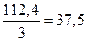
| – |
| Февраль | 36,8 | |||
| Март | 35,2 | |||
| Апрель | 38,6 | 106,6 | 35,5 | 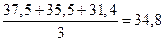
|
| Май | 29,6 | |||
| Июнь | 38,4 | |||
| Июль | 40,6 | 94,2 | 31,4 | 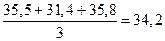
|
| Август | 20,9 | |||
| Сентябрь | 32,7 | |||
| Октябрь | 35,9 | 107,3 | 35,8 | – |
| Ноябрь | 34,6 | |||
| Декабрь | 36,8 |
Недостатком сглаживания ряда является укорачивание сглаженного ряда по сравнению с фактическим, следовательно, потеря информации.
Рассмотренные приемы сглаживания динамических рядов (укрупнение интервалов и метод скользящей средней) дают возможность определить лишь общую тенденцию развития явления, более или менее освобожденную от случайных и волнообразных колебаний. Однако получить обобщенную статистическую модель тренда посредством этих методов невозможно.
3) Метод аналитического выравнивания (количественная модель) – это метод получения сглаженной линии развития. Выравнивание заключается в подборе для данного ряда динамики теоретической кривой, наилучшим образом описывающей эмпирические данные ряда динамики. На языке математики и логики смысл этого приема заключается в том, что линия выравнивания (кривая или прямая) должна проходить в максимальной близости к фактическим уровням. Задача решается с помощью метода наименьших квадратов, то есть сумма квадратов отклонений между теоретическими (выровненными) и эмпирическими уровнями Y должна быть минимальной. При этом техника выравнивания следующая.
Задается уравнение, например, прямой линии (линейной зависимости от времени), 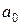 и
и 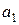 ‑ параметры прямой,
‑ параметры прямой, 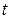 – время:
– время: 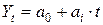 .
.
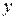 – фактические уровни ряда динамики,
– фактические уровни ряда динамики,
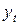 – выровненные уровни ряда динамики.
– выровненные уровни ряда динамики.
Для исходных уровней 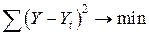 .
.
Система уравнений для нахождения параметров 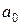 и
и 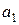 следующая:
следующая:
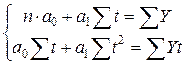
где 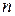 – число членов ряда динамики при
– число членов ряда динамики при 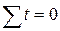 .
.
При четном числе членов ряда динамики:
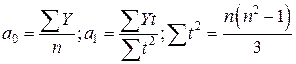 .
.
При нечетном числе уровней ряда динамики:
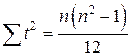 ,
,
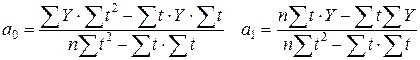 .
.
Кроме прямолинейного выравнивания ряда динамики применяются следующие наиболее часто встречающиеся зависимости:
параболы 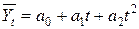 ,
,
гиперболы 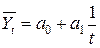 ,
,
экспоненты 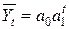 .
.
Выбор функции выравнивания производят исходя из содержательных соображений и характера данных ряда динамики. Если приросты примерно по времени равны, то выбирают линейную зависимость. Если постоянный темп прироста, то парабола и т.д.
3. Сезонные колебания. Индекс сезонности.
Определение: Устойчивые внутригодичные периодические колебания уровней ряда динамики называются сезонными колебаниями.
Само явление называется сезонностью. В экономике многие показатели подвержены сезонным колебаниям, которые изучаются с помощью индексов сезонности ( 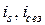 ).
).
Сезонность и сезонные колебания в экономике вызываются как социальными, так и естественно-климатическими причинами. Сезонные колебания отрицательно сказываются на развитии экономики, обуславливают неравномерность использования трудовых ресурсов и оборудования в течение года, а это в свою очередь приводит к понижению производительности труда и повышению себестоимости изготовляемой продукции.
Сезонные колебания, отраженные в рядах динамики, необходимо изучать и измерять для учета определения мероприятий, необходимых для уменьшения (или увеличения) сезонных колебаний.
Эта работа связана с разработкой приемов количественного измерения и анализа сезонности. По своему существу все методы анализа сезонности делятся на две группы:
1. Методы, с помощью которых определяется и измеряется сезонность непосредственно из эмпирических (практических) данных, без особой предварительной их обработки:
а) метод простой средней;
б) метод относительных чисел;
в) метод У. Персонса.
2.Суть методов заключается в предварительном определении и исключении общей тенденции развития и в последующем исчислении и количественном измерении сезонных колебаний (применяется в рядах динамики, уровни явлений которых имеют выраженную тенденцию увеличения (снижения) на протяжении изучаемого периода):
а) метод механического выравнивания;
б) метод аналитического выравнивания по уровням какой-либо кривой;
в) метод скользящей (подвижной) средней.
Рассмотрим некоторые из методов.
1а. Метод простой средней – применяется для анализа сезонности явлений, уровни которых не имеют резко выраженной тенденции уменьшения или увеличения. Сезонная волна определяется как процентное отношение средних квартальных (или месячных) уровней к общей средней.
МПС для расчета сезонной волны дает возможность нейтрализовать случайные колебания показателей исследуемого ряда динамики и определить сезонные колебания в среднем за весь период. Правильность получения сезонной волны зависит:
– числа уровней ряда:
– характера изменения уровней ряда.
Чем продолжительнее период анализа, чем больше число лет привлекается к расчетам, тем устойчивее будут полученные данные. Однако чем продолжительнее период анализа, тем больше проявляется тенденция увеличения или уменьшения уровней ряда динамики и на показатель сезонной волны в большей степени окажет влияние общая тенденция развития, а не сезонные колебания.
При наличии маловыраженной общей тенденции подъема уровней ряда динамики, ее влияние на сезонную волну можно уменьшить с помощью некоторого преобразования уровней ряда.
Для этого исчисляются индексы сезонности.
Определение: Индексы сезонности – это процентные отношения уровней ряда к их среднеквадратичному показателю за каждый год, а затем из полученных отношений определяется средняя арифметическая для каждого квартала за весь анализируемый период.
Пример. Имеются данные продажи сахара по Ивановскому региону. Вычислить сезонную волну методом простой средней и из процентных отношений уровней (с помощью индекса сезонности).
Решение:
Таблица 30
Анализ методов простой средней сезонности продажи сахара
по Ивановскому региону
| Годы | Кварталы | Итого за год | Среднеквартальные уровни (по годам) | |||
| I | II | III | IV | |||
| А | ||||||
| 51,87 47,99 43,02 46,29 40,03 36,35 | 54,65 48,73 49,62 47,99 40,15 39,11 | 62,31 48,03 58,44 57,17 47,34 57,27 | 54,12 46,61 48,00 45,42 35,29 47,71 | 223,25 191,36 199,08 196,87 162,81 174,44 | 55,81 47,84 49,77 49,22 40,7 43,61 | |
| Итого за 6 лет Средние уровни за 6 лет Сезонная волна | 265,55 44,26 92,58 | 280,55 46,76 97,76 | 330,56 55,09 115,18 | 271,15 45,19 94,48 | 1 147,81 191,3 | 286,96 47,83 100,00 |
6 графа вычисляется как средняя арифметическая: 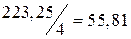 , так же вычисляются средние уровни продаж за весь период.
, так же вычисляются средние уровни продаж за весь период.
Сезонная волна определяется процентным отношением уровней поквартальных средних к средней квартальной за весь период.
Для 1 кв.: 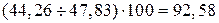 и т.д.
и т.д.
Из таблицы видно, что в 1 кв. меньше всего продавалось сахара. В среднем за 6 лет в 1 кв. продавалось на 7,42% 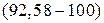 меньше средней квартальной продажи, а в 3 кв. на 15,8% больше.
меньше средней квартальной продажи, а в 3 кв. на 15,8% больше.
Таблица 31
Дата добавления: 2016-06-22; просмотров: 4659;











